Le schéma suivant représente un train d'engrenages d'un type un peu particulier :
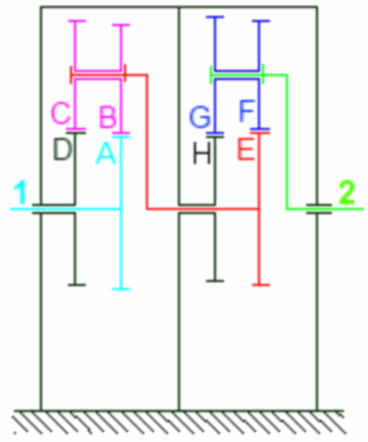
Les nombres de dents des différentes roues dentées sont :
A = 37, B = 22, C = 22, D = 38,
E = 27, F = 21, G = 21, H = 26.
Combien de tours effectue l'arbre 2 quand l'arbre 1 fait 1 tour ?
Spoiler : [Afficher le message] Les roues D et H sont liées au bâti, et donc ne tournent pas !
Spoiler : [Afficher le message] Peut-être faudrait-il savoir de quel type de train d'engrenages il s'agit ? Alors Wikipédia peut vous être d'un grand secours.
Spoiler : [Afficher le message] Au fait, les matheux, comment appelle-t-on déjà, la courbe décrite par un point quelconque de la roue B, par exemple ?
Spoiler : [Afficher le message] Ah oui ! Une épicycloïde, bon sang, mais c'est bien sûr ! Il s'agit donc d'un train épicycloïdal dont on peut calculer le rapport à l'aide de la formule de Willis  .
.
Pour ceux qui penseraient qu'il n'est pas possible de faire fonctionner deux engrenages ensemble alors que la somme des nombres de dents "A + B" (ou "E + F") est différente de la somme "C + D" (ou "G + H"), je précise que c'est tout à fait possible en effectuant sur les roues des corrections de dentures dites "avec variation d'entraxe".
(Réponse avec 3 chiffres significatifs, précédés du signe "-" si les deux arbres tournent en sens contraire.)

 Accueil
Accueil
 Forum
Forum







