Bonjour!
Amis Dédales en herbe le moment de faire travailler vos méninges pour me construire un beau labyrinthe est arrivé!
On se trouve dans le plan, en 2D donc, notre labyrinthe est constitué de salles carré unité. Si deux salles se touchent par un coté on peut passer de l'une à l'autre. Il n'y a pas de sortie c'est juste un beau labyrinthe dans lequel on peut se promener. Dans une salle se trouve le Jeune Icare, dans une autre salle se trouve le Minotaure. Pour changer, les deux ont une vision omnisciente du labyrinthe, chacun sachant à tout instant ou il se trouve et ou se trouve l'autre et connaissant par cœur la forme totale du labyrinthe. Nos deux compères se déplacent au tour par tour, Icare, puis le minotaure, puis Icare, puis le minotaure, etc... :p. A leur tour ils peuvent décider de ne pas bouger, ou d'aller dans une salle voisine. Si à un moment le minotaure se trouve dans la même salle qu'Icare, ce dernier se fait bouffer, même si c’était à lui de jouer ensuite.
Il est assez facile de concevoir un labyrinthe dans lequel avec les règles précédentes Icare peut éternellement échapper au minotaure. Une petite boucle de salle suffit:
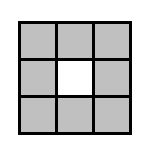
En tournant toujours dans le même sens que le minotaure Icare est sauf.
Mais seriez vous capable de me construire un labyrinthe permettant à Icare de survivre éternellement lorsqu'il y a deux minotaures? 
Précisions:
- Le placement initial des minotaures et d'Icare fait partie de la conception du labyrinthe.
- Le minotaure1 joue, le minotaure2 joue, Icare joue, et on recommence.
- Les minotaures peuvent parfaitement se trouver dans la même salle et donc se croiser.
- Il faut évidemment pouvoir survivre quelle que soit la stratégie des minotaures (parce que si c'était des quiches évidemment la question n'aurait pas d’intérêt)
Pour les hommes de peu de foi, ayant besoin de courage, voulant savoir si c'est au moins possible:
Spoiler : [Afficher le message] Oui c'est possible.
Ajout d'un indice/aide:
Spoiler : [Afficher le message] La contrainte des salles carrées est plus polluante qu'autre chose, il est plus facile de commencer par chercher un graphe (les joueurs se déplaçant sur les nœuds de celui ci, les mouvements autorisés étant symbolisés par les arêtes). Dans un second temps on peut adapter avec des salles carrées.

(Une image pour faire joli parce que c'est mieux les énigmes avec des images)
Bonne chance!
Solution:
Spoiler : [Afficher le message]
Voici quelques remarques autour de la question initiale (j'ai été inspiré), ainsi que la solution de l’énigme originelle. Il est assez commode au départ de ne pas se contraindre à utiliser des salles carrées unité mais à utiliser un objet mathématique beaucoup plus souple: les graphes.
Rappel: Un graphe c'est juste un ensemble de nœuds, dont certaines paires sont reliées par des arrêtes. Un nœud symbolisera une salle, une arrête entre deux nœuds symbolisera un déplacement possible de l'un à l'autre. Un graphe est dit planaire lorsqu'on peut le dessiner sur une feuille sans se faire croiser des arrêtes.
A) Quelques remarques avec des graphes
A.1) Sans se forcer à être planaire
Le graphe de Petersen:
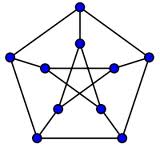
La figure est trompeuse, ce graphe est parfaitement symétrique, tous les nœuds jouent le même rôle, toutes les arrêtes également.
C'est certainement le plus petit graphe dans lequel Icare pourrait échapper aux minotaures.
Démonstration: Chaque nœud a 3 voisins qui ne sont pas voisins entre eux, ni par l’intermédiaire d'un seul autre nœud. Ainsi donc lorsqu'il est menacé Icare à toujours une échappatoire valide car inoccupée, non menacée.
Les graphes issue des sommets/arrêtes d'un tore à facette:
Selon certaines conditions ils assurent également la survie d'Icare. C'est le cas par exemple du tore à 5 sections triangulaires, du tore à 3 sections pentagonales, du tore à 4 sections carrées (Validés par programme), et des tores strictement plus gros.
Les graphes des hyper-cubes:
Rappel: pour construire le graphe d'un hyper-cube en dimension N à partir du graphe d'un hypercube en dimension N-1 vous clonez ce dernier, puis vous reliez chaque nœud à son clone. Ainsi donc la famille de ces graphes commence par: un seul nœud, un segment de 2 nœuds, un carré, un cube, etc... Un hyper-cube en dimension 3 c'est simplement un cube.
Cette famille est intéressante car elle donne une solution quelque soit le nombre de minotaures! S'il y a k minotaures, Icare peut éternellement leur échapper sur un hyper-cube de dimension 2*k (Démontré. Même genre d'argument que pour Petersen)
Le tesseract, (l'hyper-cybe de dimension 4) assure la survie d'Icare dans le cas deux minotaures.
A.2) Avec la contrainte planaire
Le graphe du dodécaèdre (trouvé grâce à Moriss):
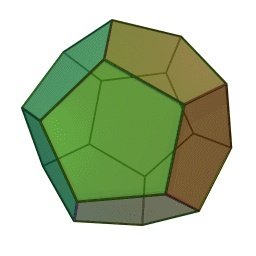
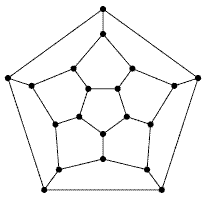
Le graphe issue des sommets/arrêtes du dodécaèdre est planaire. C'est certainement le plus petit graphe planaire dans lequel Icare pourrait échapper aux minotaures.
Démonstration: Chaque nœud a 3 voisins qui ne sont pas voisins entre eux, ni par l’intermédiaire d'un seul autre nœud. Ainsi donc lorsqu'il est menacé Icare à toujours une échappatoire valide car inoccupée, non menacée.
Une famille de graphe à moi:

C'est celle qui m'a permis de trouver la solution de l'énigme originelle. Il s'agit de toute une famille de graphes qu'on peut obtenir en faisant varier certains paramètre de la figure ci dessus. Ça ressemble à une toile d’araignée, composé de 3 orbites. On peut changer, le nombre de secteurs K, le nombre de nœuds intermédiaires d'une orbite à l'autre J, ainsi que les nombres de nœuds intermédiaires S et L. Vous remarquerez que l'orbite interne et l'orbite externe joue le même rôle. Dans cette famille, Icare s'en sort lorsque les paramètres sont biens choisis, ma conjecture: K >= 5, L > S, J >= L-S assure la vie éternelle.
Sur la figure à droite, le plus petit graphe de la famille qui assure longue vie à Icare (Validé par programme). Dans cette famille de graphes certains graphes se dessinent bien avec des salles carrées unité.
B) Version originelle de l'énigme avec des salles carrées unité.
Il est moins dur qu'on ne croit de passer d'un graphe planaire à la version salle carrée. D'une part on dispose de la possibilité de transformer des arrêtes du graphe en une succession de K nœuds. A priori faire ceci sur chaque arrête avec le même K ne change pas ses propriétés pour Icare. On ne peut certes pas rallonger les distances mais on peut raccourcir en faisant des circonvolutions avec des chaînes de salles.
Une solution avec des salles carrés unité (Validée par programme):
(le graphe de ma famille de graphe avec les paramètres K=6 S=21 L=23 J=2.)
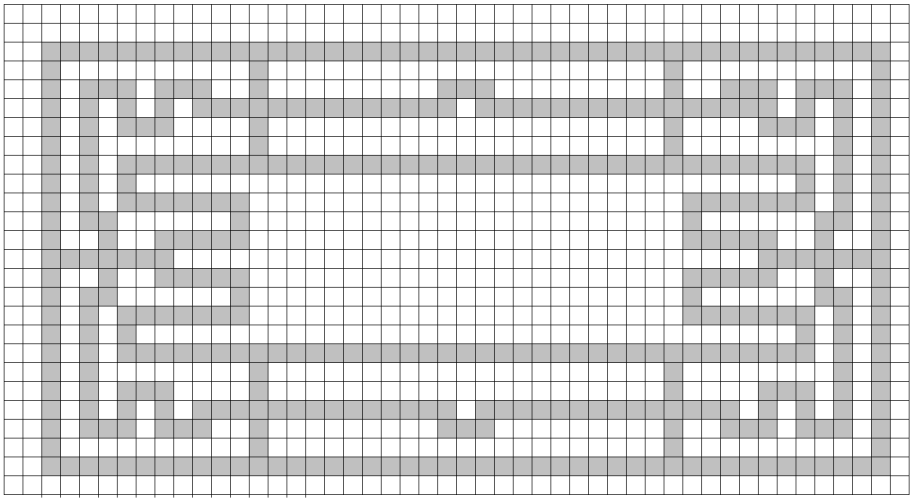
(image zoomable)
C) Validation par programme
Avec un problème de ce genre on se demande bien ce qu'on peut faire comme validation par programme, qui ne prennent pas 3 ans et soit correcte. Étonnamment il y a un argument très abordable:
Sur un graphe donné, pour une position donnée des minotaures on va appeler "death zone" l'ensemble des nœuds ou même si Icare joue le premier les minotaures peuvent finir par le capturer. (Si nos deux minotaures sont sur une chaîne de nœuds sans échappatoire, la death zone contient au moins les nœuds entre eux par exemple). A notre grande surprise il y a une relation récursive entres les death zones: La death zone d'une position des minotaures c'est l'union des death zones des positions voisines à laquelle on retire les nœuds qui touchent au moins un nœud qui ne soit pas dans cette union (on retire la surface), je vous laisse comprendre pourquoi, ce n'est pas si dur.
Après il suffit d'initialiser les death zones aux couples de cases ou se trouve les minotaures, puis a appliquer la relation ci dessus entre toutes les death zones jusqu'à ce que plus rien n'évolue. Si après la death zone d'une position quelconque des minotaures est tout le graphe, alors toutes les death zone sont tout le graphe et le graphe ne convient pas pour faire survivre Icare, dans le cas contraire, rock-n-roll!
Le bouton spoileur pour afficher la solution est plus haut 

 Accueil
Accueil
 Forum
Forum












