Bonjour,

1) Considérons le quadrillage carré suivant, dont les côtés comportent un nombre pair de cases (quelconque), et dont les deux cases aux extrémités ont été retirées. Est il possible de recouvrir ce quadrillage de dominos?
Un domino occupe deux cases adjacentes, jamais en diagonale, ils ne se chevauchent jamais, et n'occupent jamais l'un des deux coins supprimés.
Un exemple de début de recouvrement est donné par les dominos rouges.

2) Considérons le jeu suivant:

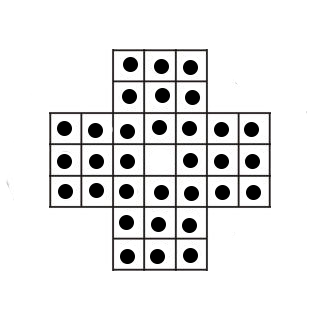
On dispose d'un plateau en croix tel que sur chaque case, il y a un pion, sauf sur la case centrale ou il a été retiré. A chaque étape, on déplace un pion au dessus d'un autre, de manière à manger le pion.
Un mouvement est valide si:
- Il y a deux cases adjacentes avec chacune un pion
- la case derrière ces deux pions est libre

Un pion ne peut en manger qu'un seul à la fois. Le pion mangé est retiré du plateau. Le pion mangeur est placé sur la case qui était vide. Les cases ou était le mangeur et le mangé sont désormais vide.
Un pion ne peut pas sortir des limites du plateau pour manger, les 3 cases concernées par un mouvement sont alignées, il ne peut jamais y avoir plus d'un pion sur la même case.
Voici un exemple de mouvement que l'on peut faire au tout début (c'est d'ailleurs le seul possible à la symétrie près)

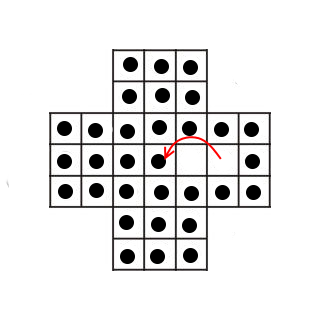
On remarque qu'à chaque mouvement, le nombre de pions sur le plateau diminue de un.
Le but est de manger tout les pions de manière à ce qu'il n'en reste plus qu'un (qui ne pourra évidemment plus manger). Lorsqu'il n'y a plus de mouvement possible, la partie est terminée (tout les pions sont isolés, ou si ils sont sur un même ligne, les extrémités de la ligne touchent les bords du plateau). Elle est gagnée s'il reste un pion, perdue si il en reste plusieurs (et vous avez triché s'il en reste zéro... )

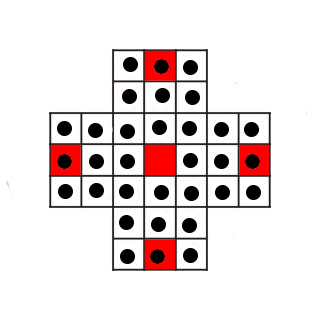
Démontrer qu'en cas de victoire, le pion gagnant ne peut se situer que sur l'une des cases en rouge.