Hello les gens!
Imaginez voir une forme polygonale qui peut s'entourer avec des copies d'elle même sans laisser de segment à l'air libre. C'est facile un simple carre ça marche, vous l'accolez à 4 copies de lui même dans les 4 directions.
Mais le nombre clef est ici 4. Le jeu c'est de faire moins. Non seulement c'est faisable mais en plus on peut atteindre 2 ce qui est clairement le minimum.
Cette tuile par exemple le fait:
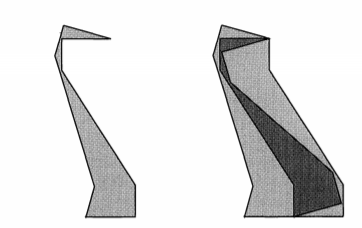
(Elle est bien d’épaisseur non nulle partout "Voderberg Tile")
Et donc mon défi:
Trouver un polyomino qui minimise le nombre de copies de lui même nécessaire pour s'entourer ainsi.
Je rappelle qu'un polyomino est un assemblage de carrés par exemple:
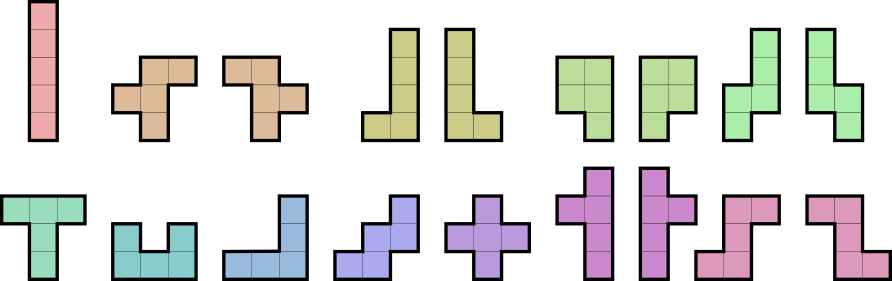
Moi ce qui m’intéresse c'est surtout d'atteindre 2, après quelques heures de réflexions et de recherche (et j'espere qu'il n'existe pas de solution triviale dans des pistes autres que celles que j'ai) je me dit que c'est pas forcement impossible. Il y a de l'espoir et a priori si la solution existe elle est satisfaisamment tordue.
Bonne chance!

 Accueil
Accueil
 Forum
Forum








