Bonjour à tous. Le groupe sécurité de mon chauffe-eau fuit, et ça m'agace, alors plutôt que de m'occuper du problème, je préfère en tirer une énigme.
Suite à une fuite, une goutte tombe régulièrement dans une gouttière. La gouttière est assimilée à une succession de cases, infinie tant à gauche qu'à droite (voir figure ci-dessous).
À l'instant t=0, toutes les cases sont vides. À l'instant t=1, une goutte est tombée dans la case centrale, et les autres cases sont vides. Puis à chaque nouvel instant, une goutte supplémentaire se rajoute à la case centrale, tandis que par ailleurs, l'eau s'étale : si une case contenait g gouttes, à l'instant suivant, ces g gouttes disparaissent de cette case en se répartissant équitablement dans les deux cases voisines, dont le total augmente ainsi de g/2.
En guise d'exemples, voici la situation aux instants t=1, 2 et 3 :
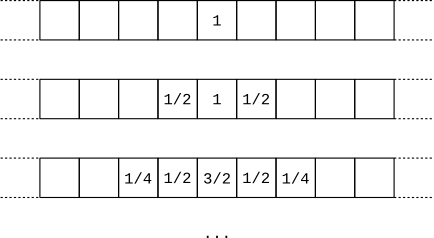
Lorsque t augmente, on a donc une quantité illimitée d'eau qui va se répartir dans un nombre illimité de cases. Or, on m'a appris en terminale que pour le calcul de limites, "∞/∞" est une forme indéterminée : étant donnée une case de ma gouttière, on peut donc imaginer que le nombre qu'elle contient ait une limite finie, ou que cette limite soit +∞, ou même qu'elle n'ait pas de limite.
Pouvez-vous déterminer le comportement de chaque case de la gouttière : admet-elle une limite, et si oui, laquelle ?

 Accueil
Accueil
 Forum
Forum







