Bonjour à tous,
Je vous propose une nouvelle petite énigme, que j'ai déjà posée sur l'ile des mathématiques (donc n'allez pas là bas pour voir la solution)
Deux p2tiens un peu sportifs décident de se faire une petite ascension d'une montagne. Comme ce n'est pas très stimulant intellectuellement, ils se lancent un petit défi : Ils doivent pendant l'ascension garder en permanence la même altitude. Cependant, ils ne marchent évidemment pas côte à côte mais attaquent chacun un versant de la montagne (qui est en 2d). Étant télépathes, la coordination ne leur pose pas problème...
Si la pente était monotone, le défi serait aisé. Cependant la montagne à gravir est un peu plus biscornue, en voici un relevé topographique (avec courbes de niveau) :
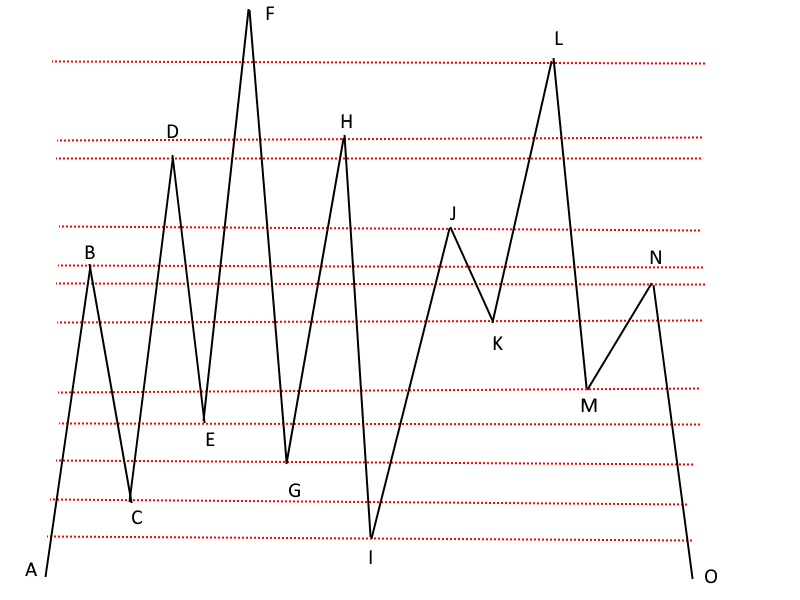
Comment peuvent-il planifier leur ascension ? L'un des deux (ou les deux) peut bien entendu choisir de rebrousser chemin pendant un moment pour pouvoir mener à bien cette mission.
Pourrons t-il toujours trouver un moyen d'arriver au sommet quel que soit le profil de la montagne ?

 Accueil
Accueil
 Forum
Forum







