Sachant sans doute que j'aimais bien me prendre la tête, on m'a offert pour Noël un "Color cube Sudoku".

Il s'agit d'un jeu de réflexion composé d'une boîte dans laquelle il faut disposer 9 cubes. Chaque cube comporte quatre couleurs parmi six :
Blanc (W), Bleu, Jaune, Orange, Rouge et Vert.
Les deux sommets opposés sont de même couleur. Chaque face offre donc à la vue quatre couleurs. La disposition des couleurs est différente sur chaque face.
Les neuf cubes présents dans la boîte combinent les couleurs :
WBJO, WBJV, WBRO, WBRV, WJOR, WJRV, BJOV, JORV et BORV.
Par exemple, le développement du cube WBRV donnerait ceci :
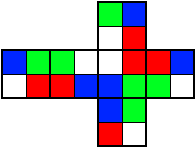
Le but du jeu est de remplir la boîte en respectant la règle du sudoku : les six couleurs doivent apparaître dans chacune des six lignes et des six colonnes (on ne doit donc pas rencontrer deux fois une même couleur dans une ligne ou une colonne).
Les habitués des Énigmes Mathématiques devant se sentir un peu frustrés actuellement, je vous propose un peu d'analyse combinatoire :
A) On peut trouver sur Internet qu'avec ces couleurs, on peut afficher sur la face supérieure de la boîte plus de 2 milliards arrangements. Pourrait-on avoir un nombre plus précis ?
B) Parmi tous les arrangements, on prétend par ailleurs qu'il existe plus de 500 000 solutions compatibles avec les règles du Sudoku. Quel en est le nombre exact ?
C) A partir d'une solution respectant les règles du Sudoku, combien de solutions différentes peut-on obtenir par combinaisons de rotations, de permutations entre les lignes ou les colonnes et de symétries éventuelles ?
D) Combien de cubes différents peut-on fabriquer à partir de ces six couleurs, en respectant la règle de la disposition différente des couleurs sur chaque face ?
E) A partir de ces N cubes, combien de arrangements existe-t-il pour remplir la boîte de 9 cubes ?
F) Parmi ces arrangements, combien de solutions respectent la règle du Sudoku ?
Je ne prétends pas connaître toutes les réponses, notamment celles sur les solutions respectant la règle du Sudoku  .
.
Amusez-vous bien. Mais vous n'êtes pas obligés d'attendre d'avoir calculé les réponses à toutes les questions pour proposer les résultats de vos cogitations  .
.

 Accueil
Accueil
 Forum
Forum








