Bonjour à toutes et à tous,
Mon père était un homme complexe, tout comme les cryptarithmes, carrés magiques parfaits et autres énigmes qu'il aimait créer. Il aurait adoré ce site !
Je souhaite partager avec vous l'un ou l'autre de ses casse-têtes pour jauger à la fois l'intérêt qu'ils pourraient susciter et leurs complexités.
Merci de partager vos impressions.
"Retrouvez l'énoncé de cette division sur base de ce développement (solution unique)".
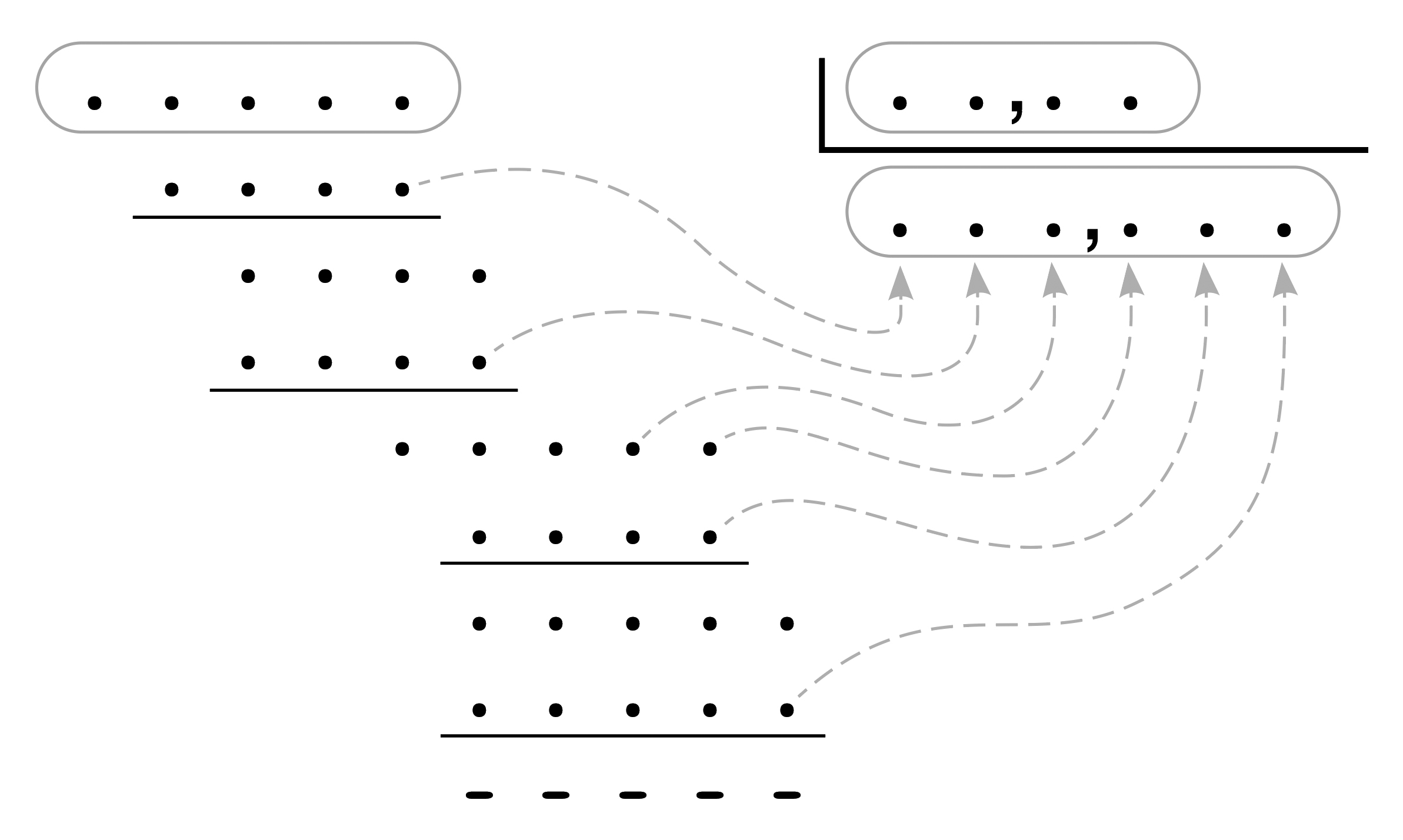
A vous de jouer, bon amusement ! (Solution en spoiler)
Spoiler : [Afficher le message]
1°)
Pour éliminer les virgules du diviseur et du quotient, on multiplie le dividende par 10⁵ ; comme le dernier chiffre de la partie décimale d’un nombre n’est jamais nul, D le nouveau diviseur ni le nouveau quotient ne sont multiples de 10 ; on met en place les chiffres imposés par la disposition et on introduit des minuscules de valeurs quelconques pour faciliter l’exposé de la solution ; la disposition montre encore que c<d
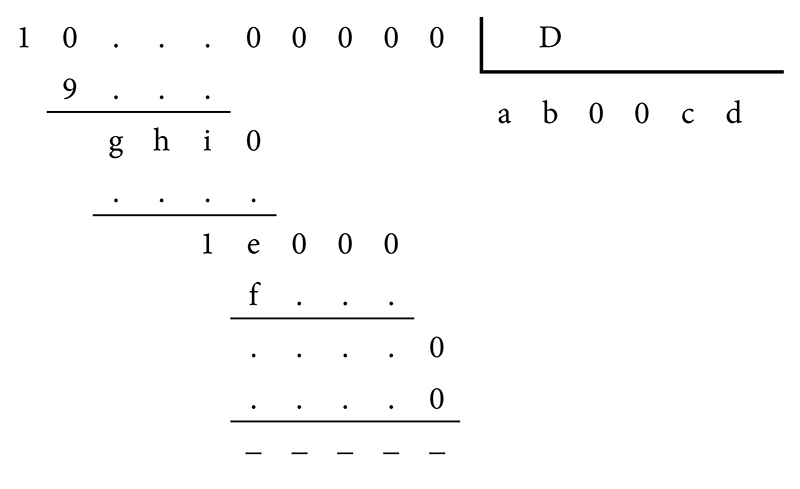
2°)
a·D = 9 . . . < 10⁴ ; c·D = f . . . = le plus grand multiple de D inférieur à 10⁴
d'où f=9 et a=c ; en effet, si, dans une division, deux produits partiels commencent tous deux par 9 (ou tous deux par 8) ils sont égaux.
3°)
cd·D = 1e·10⁴ = 1e·2⁴·5⁴ et, comme ni cd ni D ne sont multiples de 10, et comme d'autre part cd ne peut être multiple de 5⁴=625, il faut que D soit un multiple impair de 625 tandis que cd est un multiple de 2⁴=16 ; cd<10² et c<d d'où cd=16 ou 48 c'est-à-dire c=1 ou 4
4°)
b00cd·D = ghi·10⁵ = ghi·2⁵·5⁵ d'où D est un multiple impair de 5⁵=3125 mais D<10⁴ d'où D=3125 ou 9375
5°)
si D=3125, on a a=c=3 ce qui est impossible car c=1 ou 4
d'où D=9375 d'où a=b=c=1 d'où d=6 et le produit de 9375 par 110016 donne le dividende.
La solution unique est donc 10314 : 93,75 = 110,016

 Accueil
Accueil
 Forum
Forum








