On m'a posé une petite énigme très mignonne, accessible à toute personne dont le niveau est CM2 (et + évidemment  ) !
) !
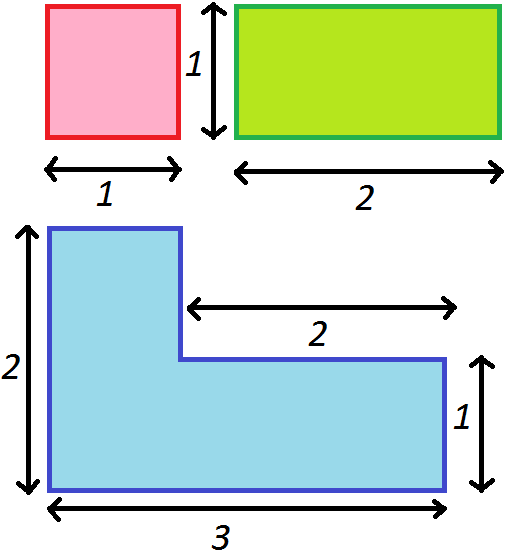
J'ai 3 petites formes toutes jolies :
- un carré ;
- un rectangle dont la longueur est égale au double de la longueur du côté du carré, et dont la largeur est égale à la longueur du côté du carré ;
- une sorte de L dont l'image et les dimensoions sont représentées ci-dessous ;
Maintenant, à partir des trois pièces de bases, construisez une autre forme admettant un axe de symétrie au moins. Il y a quelques règles cependant :
- Il faut que toutes les pièces soient présentes dans la forme ;
- On peut faire subir des rotations aux pièces ou des symétries, notamment pour le rectangle, et surtout pour le "L" ;
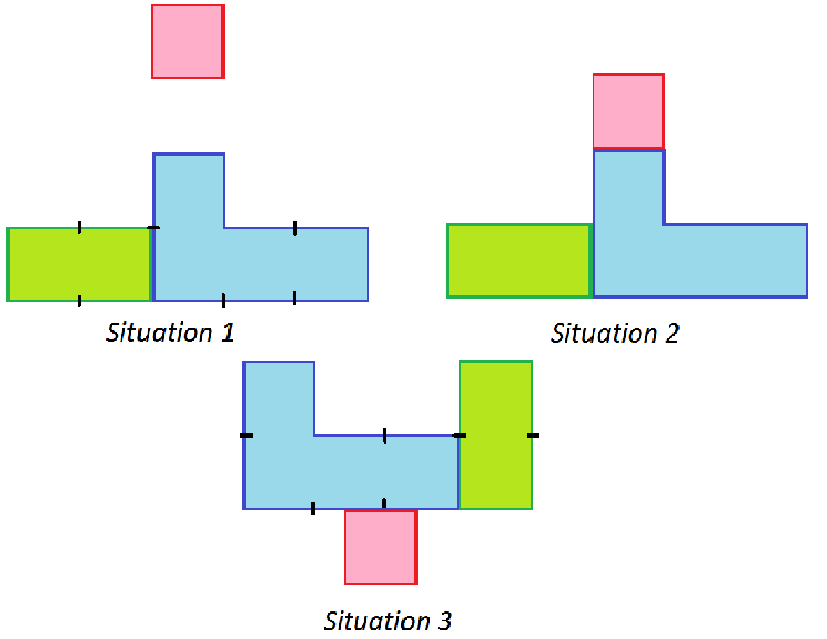
- Il faut que toutes les pièces soient collées par au moins un côté. C'est pourquoi la situation 1 ci-dessous n'est pas acceptable  même si elle admet un axe de symétrie ;
même si elle admet un axe de symétrie ;
- La situation 3 est refusée, car, même si la forme en question possède un axe de symétrie, une des formes n'est pas collée "correctement" car il faut que les côtés des formes collées soient "contenues" entre deux graduations noires. Deux graduations noires délimitent un segment égal à la longueur du carré. Je reconnais que ce n'est pas très bien expliqué, envoyez-moi un MP si vous voulez plus d'explications ;
- Il n'y a pas d'obligation dans l'orientation de l'axe de symétrie ;
Pouvez-vous trouver le plus d'assemblages possibles de manière à ce que la forme obtenue admette au moins un axe de symétrie ?
Personnellement, en plus de ma situation 2 (qui est donc bonne  ), j'en ai trouvé 11. Bonne chance !
), j'en ai trouvé 11. Bonne chance ! 
Alexein41

 Accueil
Accueil
 Forum
Forum








