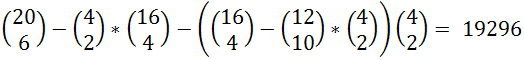Enigme Trajets sur un rectangle découpé 1/2 @ Prise2Tete

nodgim · #1

Bonjour @ tous.

On découpe dans du papier quadrillé un rectangle 14*6. On repère le pt A en (0,0) en bas à gauche et le pt B en haut à droite en (14,6). On découpe dans le rectangle 2 fenêtres carrées 2*2 centrées en (2,2 ) et (12,4).

On compte le nombre de chemins possibles (cheminement par les contours autorisé) pour aller de A à B en progressant sur le quadrillage uniquement soit vers le haut soit vers la droite.

On m'a dit qu'avec les fenêtres le nombre de chemins possibles était moins de la moitié de celui sans les fenêtres.

Qu'en pensez vous ?

Ebichu · #2

Salut nodgim,

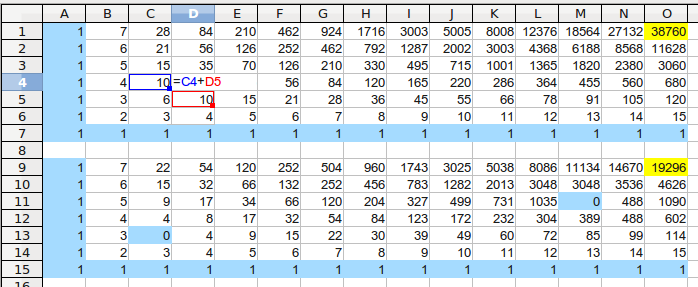
j'en pense que c'est vrai : 19296 < 38760/2

nodgim · #3

C'est bon Ebichu, et vite fait s'il vous plait !

Et sans tableur ?

enigmatus · #4

Bonjour,

nodgim a écrit:
On m'a dit qu'avec les fenêtres le nombre de chemins possibles était moins de la moitié de celui sans les fenêtres.

"On" t'a bien renseigné. Je trouve respectivement 19296 et 38760 chemins, soit moins de 49,8%.

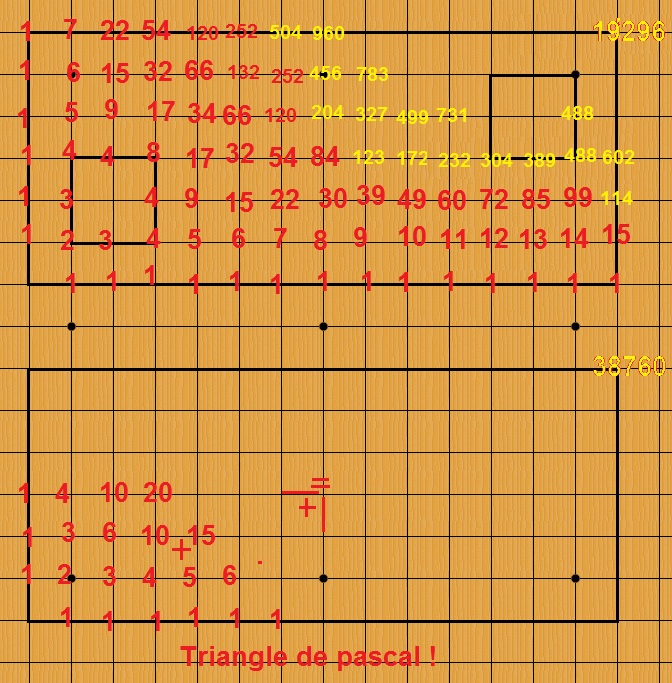
Ce calcul peut se faire à la main, de proche en proche : pour chaque point du quadrillage, le nombre de chemins est la somme des nombres de chemins arrivant au point de gauche et à celui du dessous. C'est fastidieux, et j'ai fait un scrpt en python3.

Code:

#!/usr/bin/env python3

I,J=6,14

def calcul(gri):
   for i in range(I+1):
    for j in range(J+1):
     if (i,j) in gri: continue
     if   i==0 and j==0: gri[(i,j)]=0
     elif i==0 or  j==0: gri[(i,j)]=1
     else: gri[(i,j)]=gri[(i-1,j)]+gri[(i,j-1)]

   for i in range(I,-1,-1):
    for j in range(J+1):
     print("%5s "%gri[(i,j)],end='')
    print()
   print()

calcul({(2,2):0,(4,12):0})
calcul({})

En voici le résultat :

Code:

    1     7    22    54   120   252   504   960  1743  3025  5038  8086 11134 14670 19296 
    1     6    15    32    66   132   252   456   783  1282  2013  3048  3048  3536  4626 
    1     5     9    17    34    66   120   204   327   499   731  1035     0   488  1090 
    1     4     4     8    17    32    54    84   123   172   232   304   389   488   602 
    1     3     0     4     9    15    22    30    39    49    60    72    85    99   114 
    1     2     3     4     5     6     7     8     9    10    11    12    13    14    15 
    0     1     1     1     1     1     1     1     1     1     1     1     1     1     1 

    1     7    28    84   210   462   924  1716  3003  5005  8008 12376 18564 27132 38760 
    1     6    21    56   126   252   462   792  1287  2002  3003  4368  6188  8568 11628 
    1     5    15    35    70   126   210   330   495   715  1001  1365  1820  2380  3060 
    1     4    10    20    35    56    84   120   165   220   286   364   455   560   680 
    1     3     6    10    15    21    28    36    45    55    66    78    91   105   120 
    1     2     3     4     5     6     7     8     9    10    11    12    13    14    15 
    0     1     1     1     1     1     1     1     1     1     1     1     1     1     1

Ebichu · #5

Sans tableur je dirais : [latex]\binom{20}{6}=38760[/latex] et [latex]\binom{20}{6}-\binom{4}{2}\binom{16}{4}-\left(\binom{16}{4}-\binom{4}{2}\binom{12}{2}\right)\binom{4}{2}=19296[/latex].

golgot59 · #6

Salut !

A moins que je ne me sois trompé, je trouve que c'est faux (mais proche) :

38760 chemins sans fenêtre et 19296 avec...

nodgim · #7

@ Ebichu: c'est bien en effet la formule à utiliser. Tu as fait le tour complet du problème. Bravo à toi !

@ Enigmatus et Golgot :

Ce sont les bons résultats, bravo à vous deux !
Et beau dessin pour Golgot pour qui le résultat est toujours à emballer dans un beau papier. Salut l'artiste !

Reste à tenter de trouver une justification à ces résultats.

enigmatus · #8

Dans le cas sans fenêtres, le nombre de chemins pour arriver au point de coordonnées (i,j) est C(i+j,i) (nb de combinaisons de i valeurs choisies parmi i+j).

nodgim · #9

Oui Enigmatus.
C'est à partir de cette idée qu'on arrive à trouver la solution avec les fenêtres.

Indice: soit en calculant avec des points intermédiaires, soit par soustraction.

golgot59 · #10

Je ne sais pas si c'est l'explication que tu voulais, mais le résultat du décompte avec fenêtres s'obtient par le calcul :

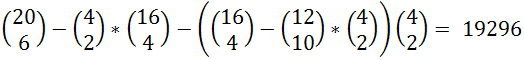
On enlève d'abord la valeur de la case en bas à gauche (2 parmis 4) qui fait 6 et qui se répèterai si elle était là 4 parmi 16 fois, puis on enlève l'autre fenêtre qui donne la soustraction un peu plus compliqué...

nodgim · #11

C'est bien Golgot, bravo à toi !

C'est toujours la même chose, ce n'est pas compliqué une fois qu'on a compris le truc.

Juju · #12

J'ai trouvé 37100 pour le nombre de chemins sans fenêtre
et j'ai trouvé 1056 avec les fenêtres.
Donc avec les fenêtres s'est bien moins de la moitié.

gwen27 · #13

Je me trompe peut-être, mais la solution a l'air relativement simple.

Sans fenêtre le nombre de chemins possibles est le nombre de manières de placer les 6 déplacements verticaux parmi les 20 nécessaires , soit C(6,20)

C(6,20) = 20 ! / ( 6! 14! ) = 38760.

En rajoutant une fenêtre en (2,2), il faut , de la même façon, retirer tous les chemins y menant soit C(2,4) multiplié par le nombre de chemins en partant.

A retirer : C(2,4) C(4,16) => C(6,20) - C(2,4) C(4,16)

On retire aussi le nombre de chemins passant par la seconde fenêtre (identique par symétrie).

A retirer : C(2,4) C(4,16) => C(6,20) - 2 C(2,4) C(4,16)

Seulement, on a retiré deux fois les chemins passant par les deux fenêtres...

A rajouter : C(2,4) C(2,4) C(2,12)

C(6,20) - 2 C(2,4) C(4,16) + C(2,4) C(2,4) C(2,12)

= 38760 - ( 2 * 6 * 1820 ) + ( 6 * 6 * 66 ) = 19296

On retire donc bien un peu plus de la moitié des chemins ( 19380 )

nodgim · #14

@ Juju :
Non. Ton nombre de chemins sans les fenêtres est proche de la vérité, mais pas ton nombre avec les fenêtres.

@ Gwen :
Parfait ! Tu as écrit exactement ce que j'avais envie de dire en conclusion. Tu es télépathe ou médium ?

Juju · #15

Rebonjour,
J'avais une erreur de calcul, avec les fenetres je trouve 38760.
Et sans les fenêtres, j'avais mal dimensionné les fenêtres, je trouve 19296.
Donc oui avec les fenêtres le nombres de chemin est moins de la moitié (38760/2=19380)

nodgim · #16

OK Juju, c'est bon maintenant, bravo à toi !

Il y a un raccourci théorique pour ce problème, qui évite le recours à du calcul algorithmique.

Ebichu · #17

Question subsidiaire : on découpe dans du papier quadrillé un rectangle 7*7. On repère le point A en bas à gauche par (0;0) et le point B en haut à droite par (7;7).

Quel est le nombre minimal de points du quadrillage qu'il faut supprimer (par exemple, dans son énoncé, nodgim avait supprimé deux points) pour que le nombre de chemins possibles pour aller de A à B soit 2018 ?

golgot59 · #18

Spoiler : [Afficher le message]

Ebichu · #19

@golgot59 : bien vu À symétrie près, c'est la seule solution.

enigmatus · #20

J'ai une autre solution : (0,5) (1,2)

Ebichu · #21

@enigmatus : je ne pense pas, ça fait 2010. Je pense que tu as mis un 1 au lieu d'un 0 en (0,6).

enigmatus · #22

Ah oui, exact.

nodgim · #23

Bon, je n'ai pas pu examiner la relance d'Ebichu, mais si ça vous intéresse, j'avais gardé par devers moi cette configuration là :

Rectangle toujours de (6,14) et fenêtre centrée au milieu de 4*2 (longueur de la fenêtre parallèle à la longueur du rectangle).

Nombre de chemins ?

Ebichu · #24

Spoiler : [Afficher le message]

golgot59 · #25

Spoiler : [Afficher le message] avec le tableur 16800

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 11-01-2018 08:55:24

trajers sur un rectangle découpé

#0 Pub

#2 - 11-01-2018 10:23:46

Trajets sur un rectanngle découpé

#3 - 11-01-2018 12:09:20

trajets sur un rectangle déxoupé

#4 - 11-01-2018 14:14:38

trajets sur un rextangle découpé

nodgim a écrit:

Code:

Code:

#5 - 11-01-2018 15:32:40

trajets sur un rectangle sécoupé

#6 - 11-01-2018 16:20:03

Trajets sur un retcangle découpé

#7 - 11-01-2018 18:07:04

Trajets sur un rectangle édcoupé

#8 - 11-01-2018 20:54:22

trajets sir un rectangle découpé

#9 - 12-01-2018 07:36:07

Trajets sur un rectngle découpé

#10 - 12-01-2018 14:45:01

Trajets sur un rectangle déoupé

#11 - 12-01-2018 17:03:07

Trajets sur un rectangl edécoupé

#12 - 12-01-2018 18:54:37

trajets sue un rectangle découpé

#13 - 12-01-2018 19:19:09

trajets sut un rectangle découpé

#14 - 13-01-2018 07:48:16

Trajets sur un rectagnle découpé

#15 - 13-01-2018 12:27:05

trajets sur un rrctangle découpé

#16 - 14-01-2018 07:47:45

Trajts sur un rectangle découpé

#17 - 14-01-2018 19:21:34

Trajets sur un recatngle découpé

#18 - 14-01-2018 20:15:57

trajets sur un recyangle découpé

#19 - 14-01-2018 21:18:02

Traajets sur un rectangle découpé

#20 - 14-01-2018 21:32:56

trajets sur un recrangle découpé

#21 - 14-01-2018 21:39:43

Trajets sur un rectangle décuopé

#22 - 14-01-2018 22:10:40

Trajet sur un rectangle découpé

#23 - 15-01-2018 16:29:40

trajets qur un rectangle découpé

#24 - 15-01-2018 16:50:20

trajets sur un rectangke découpé

#25 - 15-01-2018 17:12:23

Trajets sur un rectangle dcéoupé

Réponse rapide

Sujets similaires

Pied de page des forums