 |
#1 - 19-08-2011 18:24:47
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Math'OO
Deux disques (A de centre O et B de centre P), tangents extérieurement, pratiquent le mouvement suivant en deux temps. A commence par rouler sur B, dans le sens des aiguilles d'une montre, de façon que son centre ait tourné d'un angle @ strictement compris entre 0° et 180°, autour du point P. Ensuite, c'est au tour de B de rouler autour de A, dans le sens des aiguilles d'une montre, d'un angle @/2 autour du point O. Les disques effectuent 10 mouvements complets, après quoi ils se retrouvent pour la première fois globalement dans leur position de départ. Donnez une valeur de l'angle @ en degrés ?
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#2 - 19-08-2011 18:50:40
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
mayh'ooo
Un cycle est le mouvement de A autour de B puis B autour de A.
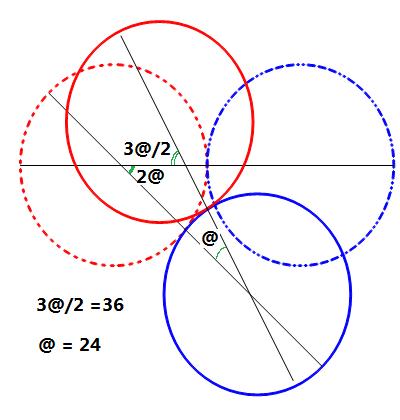
Au cours d'un cycle, le centre o de A parcourt @ puis @/2 donc 3@/2.
Donc 30@/2=360 ce qui donne @=24 degrés.
The proof of the pudding is in the eating.
#3 - 19-08-2011 18:52:13
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Math'OO
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#4 - 19-08-2011 19:45:28
- yogolo
- Passionné de Prise2Tete
- Enigmes résolues : 48
- Messages : 79
MathO'OO
24°?
Après chaque double mouvement, il me semble que la demi-droite PO tourne d 'un angle 3@/2.
En revenant à la position originale, on peut considérer que O a tourné de 360° autour de P après 10 doubles mouvements.
#5 - 19-08-2011 19:53:12
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
math'oio
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#6 - 19-08-2011 19:58:43
- yogolo
- Passionné de Prise2Tete
- Enigmes résolues : 48
- Messages : 79
Math'OOOO
On demande UNE valeur de @
Pour être plus complet on peut dire:24° et multiples de 24°...
#7 - 19-08-2011 20:15:00
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Maath'OOO
Tous les multiples, yogolo ?
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#8 - 19-08-2011 20:28:54
- yogolo
- Passionné de Prise2Tete
- Enigmes résolues : 48
- Messages : 79
marh'ooo
24°, 48°, 72°, 96°, 120°, 144° et 168°
Eventuellement 0° si la condition "compris entre 0° et 180° " admet inclus.
#9 - 19-08-2011 20:32:06
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Math'OOOO
Non, là, c'est faux. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#10 - 19-08-2011 21:01:00
- yogolo
- Passionné de Prise2Tete
- Enigmes résolues : 48
- Messages : 79
Math'OO
Exact, j'ai oublié le "pour la première fois"
Bilan et j'espère n'avoir rien oublié, je fatigue:
24°,72° et 168°.
#11 - 19-08-2011 21:06:09
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
math'ioo
Oui, là, c'est juste. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#12 - 19-08-2011 22:42:14
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
math'ioo
Bonjour,
Je considère l'angle que fait le vecteur PO par rapport à un repère fixe. Cet angle augmente de @ lorsque A roule et de @/2 (dans le même sens) lorsque B roule. Au bout de 10 mouvements, il aura augmenté de 15@, qui sera égal à 360° pour retrouver la position initiale, et donc @ = 24°
Bonne soirée.
Frank
Edit: Ma réponse me semble trop simple, mais je cherche encore le piège !!!
#13 - 20-08-2011 10:32:35
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
marh'ooo
Mais pas sûr d'avoir bien compris le problème 
Parce que sinon @= 72° et @=168° fonctionnent aussi.
#14 - 20-08-2011 11:50:15
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
ath'OOO
Ce problème ne vous a pas fait tourner en rond trop longtemps... J'adore quand vous êtes surpris de la simplicité du problème. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#15 - 20-08-2011 19:20:06
- esereth
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 176
Math''OOO
Bonsoir,
Intuitivement, je dirais 72 degrés. Ou 36 si les deux cercles ont même rayon, ce qui rendrait la configuration formée par les deux cercles globalement identique au bout de 5 étapes avec 72 degrés.
Un calcul à l'aide des complexes doit permettre de le prouver mais c'est pénible à écrire sur un Iphone. J'attends de savoir si c'est bon pour me lancer.
#16 - 20-08-2011 19:56:57
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Mat'OOO
Disons que ce n'est pas la seule solution, esereth... 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#17 - 20-08-2011 22:41:08
- esereth
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 176
Mat'hOOO
Je corrige après un passage par Geogebra :
Les solutions sont les multiples de 24 degrés.
24,48,72,96,120,144 et 168.
Mon approche complexe était entachée d'une erreur.
En notant z_0 et p_0 les affixes de O et P et z_n et p_n celles des points atteints par O et P après n étapes, on a :
z_n+1 - p_n = e^(-i@)(z_n - p_n)
p_n+1 - z_n+1 = e^(-i@/2)(p_n - z_n+1)
En rentrant la première dans la seconde,
p_n+1 - z_n+1 = e^(-3i@/2)(p_n - z_n)
De ce fait
p_n - z_n = e^(-3in@/2)(p_0 - z_0)
Si au bout de 10 étapes, on est revenu à la configuration de départ on doit avoir
p_0 - z_0 = e^(-15i@)(p_0 - z_0)
Cela impose :
15@ = 2k pi
Soit @ est un multiple de 2 pi / 15.
#18 - 20-08-2011 23:46:16
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
matj'ooo
Non, pas tous les multiples, justement. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#19 - 21-08-2011 15:28:27
- esereth
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 176
Math'OO
OK, j'avais bien vu que c'était une condition nécessaire mais je n'avais pas analysé la réciproque. En fait ce sont les valeurs de 2k pi /15 où k est premier avec 10, donc k=1, k=3 et k=7
c'est-à-dire 24, 72 et 168
Mais je n'ai toujours pas démontré pourquoi les cercles reviennent exactement à la même place.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







