Soient 3 points A, B et C non alignés dans un plan muni d'une norme "distance".


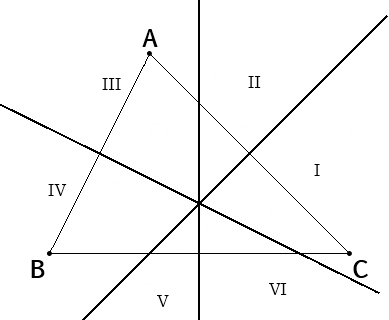
Pourriez-vous définir N points Pi dans ce plan (par exemple N = 10) et une fonction à valeur numérique $F$ tels que :

   $F$(A,Pi,B)   <   $F$(B,Pi,A)  avec  $F$(A,Pi,B) + $F$(B,Pi,A)  $\leq$  N

   $F$(B,Pi,C)   <   $F$(C,Pi,B)  avec  $F$(B,Pi,C) + $F$(C,Pi,B)  $\leq$  N

   $F$(C,Pi,A)   <   $F$(A,Pi,C)  avec  $F$(C,Pi,A) + $F$(A,Pi,C)  $\leq$  N  ?

(Quand j'écris Pi je ne parle pas de la fameuse constante mais de l'ensemble des points P indice i !
Quand je dis "<", cela veut bien dire strictement inférieure.)

Question subsidiaire : quelle est la plus petite valeur de N pour laquelle on peut écrire cette triple inégalité ?

Spoiler : [Afficher le message] Si vous ne trouvez pas, regardez du coté de l'énigme "Choix d'une automobile" ; cela a un certain rapport certain.

Spoiler : [Afficher le message] En plus d'appartenir à l'ensemble des nombres réels, les valeurs des fonctions $F$ appartiennent à l'ensemble des entiers naturels et sont comprises dans l'intervalle [0,N].

Vous pouvez faire un copier-coller de la figure dans votre Paint préféré pour y placer vos N points.