Bonjour, bonne année 
En cette nouvelle année, voici une petite recherche mathématiques rigolote.
Imaginons que nous plions une feuille en deux vers la droite puis que nous regardons la forme obtenue une fois relâchée nous obtenons une figure. Nous répétons cette opération c'est à dire on plie toujours vers la droite.
Evidemment en pratique au bout du 3ème ou 4ème pliage, il nous serait impossible de continuer mais dans notre monde théorique des maths on va supposer que l'on peut continuer ainsi à l'infini.
Sur le dessin ci dessous je vous ai présenter les premières étapes.
http://www.prise2tete.fr/upload/gilles355-mathej.jpg
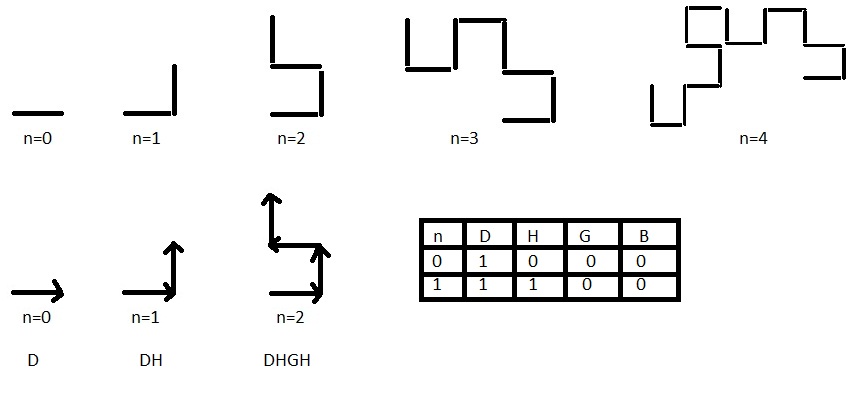
J'ai fléché le parcours, on obtient donc à l'étape 0 ( quand on n'a pas encore plié la feuille ) une flèche vers la droite, pour l'étape 1, une flèche vers la droite et une vers le haut etc.
Ma première question est pouvez vous me dire combien y aura t-il de flèches vers la droite, le haut, la gauche et le bas au bout du 8ème pliage.
Réponse à valider dans la case réponse sous le format DxxHyyGzzBww où xx est le nombre de flèches à droite, yy le nombre de flèche vers le haut etc.
La deuxième question est pouvez vous me donner une formule ou explication pour le nième pliage ?
Enfin pour ceux qui aiment les jolis dessins, pouvez vous me représenter la forme des pliages si on alterne un pliage vers la droite puis un vers la gauche etc.
Voilà amusez vous bien et n'hésitez pas à me poser des questions 

 Accueil
Accueil
 Forum
Forum







