Hello!
Ça faisait un bail que je n'avais rien posté alors voici une vraie saloperie:
-On a devant nous un polygone.
-Sur chaque sommet de ce polygone il y a un entier relatif.
-La somme de tous les sommets du polygone est strictement positive.
-On a le droit d'effectuer l'action suivante:
Action autorisée:
-On prend un sommet strictement négatif de notre choix.
-On retire le signe - (ainsi si c'est -5 on écrit 5 à la place)
-On ajoute l'entier négatif initial à chaque sommet voisin (ce qui conserve donc la somme globale)
Par exemple:
Si on a ... 2 -1 -3 4 0 ... quelque part sur notre polygone, on a le droit de prendre le -3 de le transformer en 3 et de soustraire 3 à ses deux voisins ce qui donne:
... 2 -4 3 1 0 ...
Il s'agit de démontrer que quoi qu'on fasse on ne pourra plus rien faire au bout d'un moment. (ie quoiqu'on fasse on finira par avoir que des entiers positifs ou nuls partout).
C'est assez dur d'avoir la bonne idée, mais lorsqu'on l'a ce n'est pas très long.
Je vous laisse mariner et je donnerais des indices dans un second temps.
Comme promis un premier indice (vraiment pas un très gros indice):
Spoiler : [Afficher le message] En fait il est assez difficile dans ce problème de trouver une quantité entière qui va strictement décroître à chaque opération (un monovariant). Par contre on peut utiliser le même genre d'argument mais en plus général: Il faut chercher à transformer le problème, le voir différemment de telle manière que sur son homologue transformé l'effet de l'action autorisée mène d'avantage trivialement à un état final.
2ème indice (indice moyen):
Spoiler : [Afficher le message] Sommes partielles
3eme indice (gros indice):
Spoiler : [Afficher le message] Prendre un sommet de référence sur le polygone, et regarder la suite des sommes partielles depuis ce sommet dans le sens de parcourt de votre choix.
Bonne chance!
Solution:
Spoiler : [Afficher le message] On va noter les entiers sur le polygone x0,..,xn et S leur somme.
On va prendre comme référence une arrête et on va construire la séquence
des sommes partielles dans les deux sens:
On considéré qu'on a 0 sur notre arête, puis on parcourt le polygone dans le sens horaire on fait somme de tout ce qu'on rencontre, ça nous donne la moitie droite d'une séquence infinie, pour avoir la moitie gauche on part de notre arrête on va dans le sens inverse du sens horaire et on soustrait tout ce qu'on rencontre.
Ça ressemble a ceci:
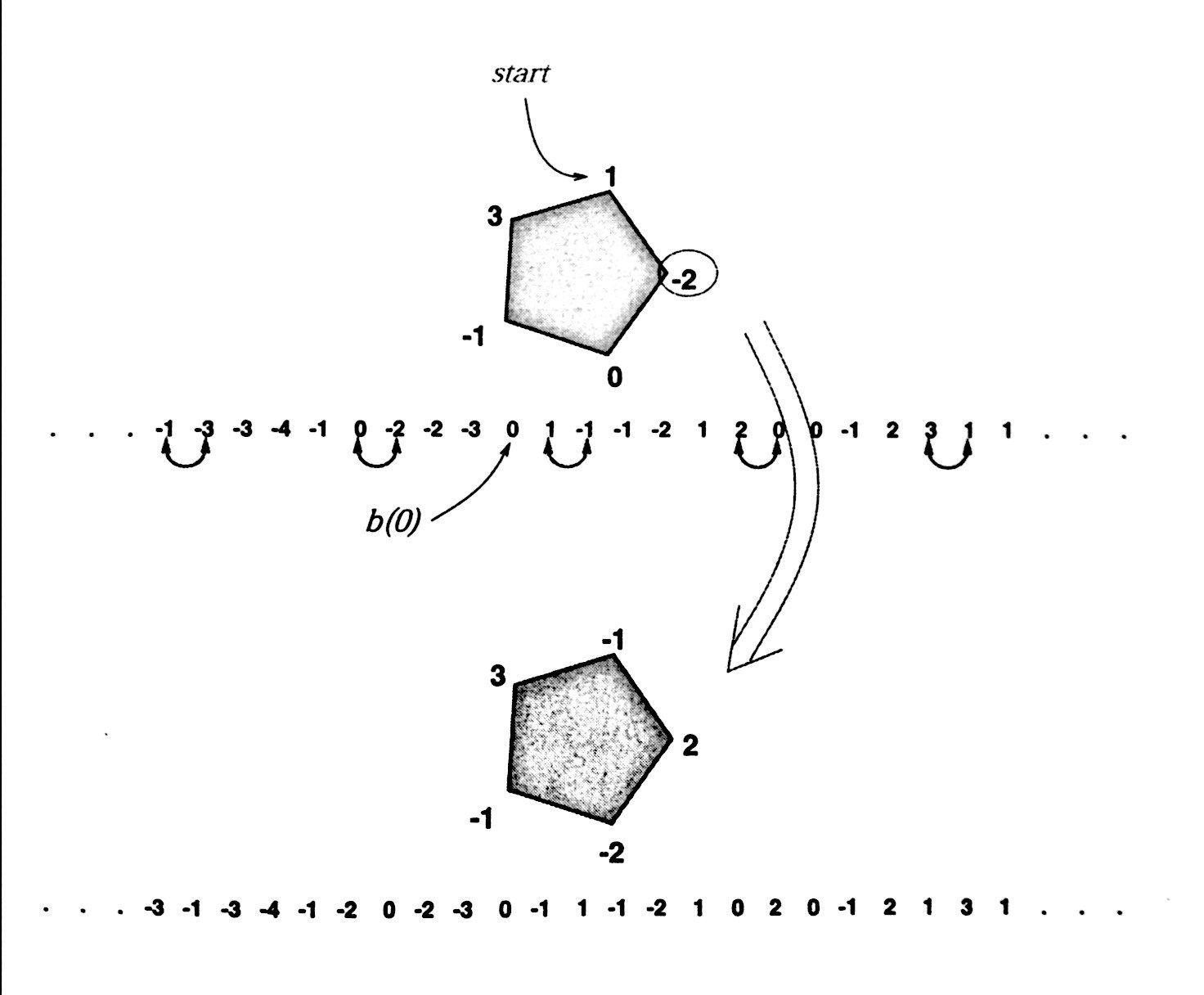
Bref on construit la séquence des sommes partielles dans les deux sens, on va la noter b(i)
-Elle est globalement croissante car S est strictement positive.
-Elle est décroissante localement si et seulement si xi est négatif.
-Lorsqu'on effectue une opération sur le polygone, ça revient à permuter deux valeurs consécutives pas dans l'ordre dans notre séquence, pour les trier par ordre croissant.
Il s'agit donc d'un tri par bulle (pour les informaticiens) et il est intuitivement facile de se convaincre qu'il va terminer en temps fini, avec comme résultat d'avoir strictement trié la liste.
Si on veut démontrer rigoureusement qu'il termine:
On peut noter i+ le nombre d'indices j>i tel que b(j) < b(i)
i+ est fini (car la suite est globalement croissante) et ne dépend que de i modulo n.
Soit P la somme des i+ sur une période, lorsqu'on permute b(i+1) alors i+ décroît de exactement 1 et les autre j+ sont inchangés, ainsi donc P décroît de 1 et le tout s’arrête lorsque P = 0 et que la liste est parfaitement triée.
Source: Mathematical Puzzles: A Connisseur’s Collection solution de Bernard Chazelle of Princeton.
Voila voila.

 Accueil
Accueil
 Forum
Forum







