|
#1 - 04-11-2015 14:26:37
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le poygone flippant
Hello!
Ça faisait un bail que je n'avais rien posté alors voici une vraie saloperie:
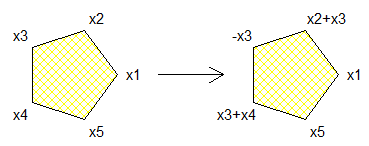
-On a devant nous un polygone.
-Sur chaque sommet de ce polygone il y a un entier relatif.
-La somme de tous les sommets du polygone est strictement positive.
-On a le droit d'effectuer l'action suivante:
Action autorisée:
-On prend un sommet strictement négatif de notre choix.
-On retire le signe - (ainsi si c'est -5 on écrit 5 à la place)
-On ajoute l'entier négatif initial à chaque sommet voisin (ce qui conserve donc la somme globale)
Par exemple:
Si on a ... 2 -1 -3 4 0 ... quelque part sur notre polygone, on a le droit de prendre le -3 de le transformer en 3 et de soustraire 3 à ses deux voisins ce qui donne:
... 2 -4 3 1 0 ...
Il s'agit de démontrer que quoi qu'on fasse on ne pourra plus rien faire au bout d'un moment. (ie quoiqu'on fasse on finira par avoir que des entiers positifs ou nuls partout).
C'est assez dur d'avoir la bonne idée, mais lorsqu'on l'a ce n'est pas très long.
Je vous laisse mariner et je donnerais des indices dans un second temps.
Comme promis un premier indice (vraiment pas un très gros indice):
Spoiler : [Afficher le message] En fait il est assez difficile dans ce problème de trouver une quantité entière qui va strictement décroître à chaque opération (un monovariant). Par contre on peut utiliser le même genre d'argument mais en plus général: Il faut chercher à transformer le problème, le voir différemment de telle manière que sur son homologue transformé l'effet de l'action autorisée mène d'avantage trivialement à un état final.
2ème indice (indice moyen):
Spoiler : [Afficher le message] Sommes partielles
3eme indice (gros indice):
Spoiler : [Afficher le message] Prendre un sommet de référence sur le polygone, et regarder la suite des sommes partielles depuis ce sommet dans le sens de parcourt de votre choix.
Bonne chance!
Solution:
Spoiler : [Afficher le message] On va noter les entiers sur le polygone x0,..,xn et S leur somme.
On va prendre comme référence une arrête et on va construire la séquence
des sommes partielles dans les deux sens:
On considéré qu'on a 0 sur notre arête, puis on parcourt le polygone dans le sens horaire on fait somme de tout ce qu'on rencontre, ça nous donne la moitie droite d'une séquence infinie, pour avoir la moitie gauche on part de notre arrête on va dans le sens inverse du sens horaire et on soustrait tout ce qu'on rencontre.
Ça ressemble a ceci:
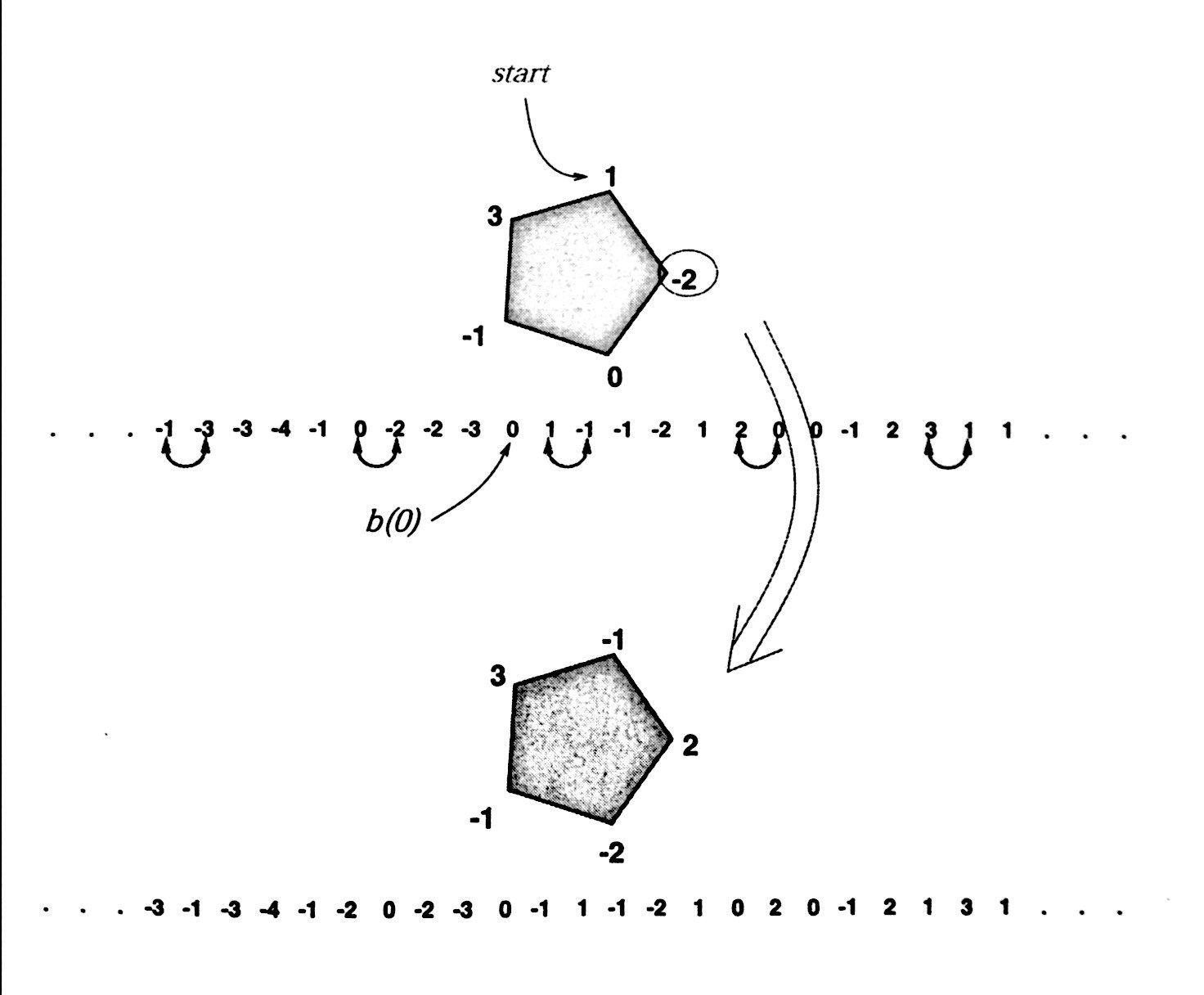
Bref on construit la séquence des sommes partielles dans les deux sens, on va la noter b(i)
-Elle est globalement croissante car S est strictement positive.
-Elle est décroissante localement si et seulement si xi est négatif.
-Lorsqu'on effectue une opération sur le polygone, ça revient à permuter deux valeurs consécutives pas dans l'ordre dans notre séquence, pour les trier par ordre croissant.
Il s'agit donc d'un tri par bulle (pour les informaticiens) et il est intuitivement facile de se convaincre qu'il va terminer en temps fini, avec comme résultat d'avoir strictement trié la liste.
Si on veut démontrer rigoureusement qu'il termine:
On peut noter i+ le nombre d'indices j>i tel que b(j) < b(i)
i+ est fini (car la suite est globalement croissante) et ne dépend que de i modulo n.
Soit P la somme des i+ sur une période, lorsqu'on permute b(i+1) alors i+ décroît de exactement 1 et les autre j+ sont inchangés, ainsi donc P décroît de 1 et le tout s’arrête lorsque P = 0 et que la liste est parfaitement triée.
Source: Mathematical Puzzles: A Connisseur’s Collection solution de Bernard Chazelle of Princeton.
Voila voila.
#2 - 04-11-2015 14:53:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Le polygone flippat
Bonjour
Il y a clairement un invariant dans le problème ( la somme des valeurs des sommets ) . Il reste à fabriquer une fonction des sommets à valeurs entières qui décroit à chaque opération .
J'ai une petite idée mais pas le temps d'approfondir , @+
Vasimolo
Edit 1 : il me semble que ça marche même si les valeurs ne sont plus entières .
Edit 2 : je crois que j'ai trouvé , je rédigerai la solution plus tard .
#3 - 05-11-2015 21:26:09
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le polyogne flippant
Comme promis un premier indice (vraiment pas un très gros indice):
Spoiler : [Afficher le message] En fait il est assez difficile dans ce problème de trouver une quantité entière qui va strictement décroître à chaque opération (un monovariant). Par contre on peut utiliser le même genre d'argument mais en plus général: Il faut chercher à transformer le problème, le voir différemment de telle manière que sur son homologue transformé l'effet de l'action autorisée mène d'avantage trivialement à un état final.
#4 - 05-11-2015 21:58:52
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Le polygonne flippant
J'avais essayé d'étudier la somme des valeurs absolues et la somme des valeurs absolues des différences consécutives qui étaient 2 notions sympa d'écrêtement mais ça marche pas ainsi que des solutions analogues qui ont abouties dans ma corbeille à papier.
Ma deuxième idée est de montrer que :
1 )on ne peut pas revenir a un état quand on y est déjà passé (forcément vrai, sinon on pourrait trouver des trajectoires cycliques et le résultat serait faux)
2 ) il y a un nombre fini de possibilités pour les cases (vrai également si le résultat l'est). Il s'agit par exemple de borner les valeurs.
et de conclure avec le "théorème du tiroir" que on s'arrête à un moment, donc forcement quand tous les nombres sont positifs.
Mais je ne démontre ni le 1) ni le 2)...
Pour le 2 ) je pense que aucun nombre en valeur absolue ne peut être supérieur à la somme des valeurs absolues initiales donc il faut plutôt se pencher sur 1)
Bonne piste ?
______
"En fait il est assez difficile dans ce problème de trouver une quantité entière qui va strictement décroître à chaque opération"
j'en ai une :
Spoiler : [Afficher le message] ma sérénité
#5 - 05-11-2015 22:48:11
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
ke polygone flippant
Quand le brillant Clydevil annonce que c'est une "vraie saloperie", je lui fais confiance et attends sagement la solution. 
#6 - 06-11-2015 10:15:07
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
le polygine flippant
On assimile une opération à :
1) un déplacement de la valeur "réelle" négative vers le voisin gauche.
2) un déplacement de la valeur négative "fantôme" vers le voisin droite.
3) la création d'une valeur positive "fantôme" égale à la valeur négative. Donc toute valeur négative contient une valeur positive fantôme.
Pour toutes les valeurs négatives réelles, on établit une relation réelle fléchée gauche vers une valeur positive. On part d'une valeur négative réelle de référence, et on établit la relation avec la 1ère valeur positive réelle rencontrée à gauche. Si la valeur négative réelle est supérieure en valeur absolue à la valeur positive réelle, on établit une nouvelle relation au départ du négatif vers le positif suivant, voire une 3ème relation,...Quand on a établi toutes les relations nécessaires au départ de catte valeur réelle négative, on recommence avec la 1ère autre valeur négative réelle à droite de la référence. La 1ère relation de cette seconde valeur négative réelle visera la 1ère valeur ou le premier reste de valeur positive réelle disponible à gauche. Comme il y a au total plus de positif que de négatif, toutes les valeurs réelles négatives seront en relation avec une (ou plusieurs) valeur positive réelle.
On réalise le même enchaînement pour les valeurs fantômes: valeurs négatives fantômes vers valeurs positives fantômes. La relation est cette fois fléchée vers la droite. A remarquer qu'ici, quand on aura établi toutes ces relations, le solde sera nul, car la somme des négatifs fantomes est égale à celle des positifs fantômes.
Chaque opération diminue la longueur de chaque relation établie. Quand la longueur d'une relation est à zéro, comme il y a rencontre de + et -, il y a effacement de la relation. L'ensemble des relations est donc convergent vers zéro, et donc les opérations s'arrêtent quand il n'y a plus de relations.
#7 - 06-11-2015 11:09:33
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le polygone filppant
@portugal: La démarche est bonne, par contre je ne sais pas si elle peut aboutir (la solution que j'ai suis une autre démarche, mais ça n'invalide pas les autres manières de faire)
@Franky1103: Lol
@Vasimolo: "il me semble que ça marche même si les valeurs ne sont plus entières ."
Oui ca marche aussi.
@nodgim: Je crois que j'arrive a me représenter ce que tu décris, mais j'ai l'impression que la conclusion est trop rapide. Oui il y a qq chose qui décroît strictement dans tes "relations" mais comme ton procédé peut faire apparaître pendant qu'il se déroule de nouvelles relations on ne peut pas conclure. (Le nombre de fantômes changent, le nombre de réels changent). Non?
#8 - 06-11-2015 13:37:26
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Le polgone flippant
Salut Clydevil: non, les relations ne doivent surtout pas changer. Elles sont établies au départ et ne font que rétrécir ou disparaitre. Dans mon modèle, les relations fixent les objets (valeurs positives ou négatives) aux 2 extrémités. Les objets négatifs se déplacent, les objets positifs sont immobiles.
Tu aurais pu poser ce problème là: quand on actionne une valeur négative, celle ci est déplacée à gauche (ou à droite), et il reste 0 à l'emplacement de l'action. On aboutirait au même résultat final.
#9 - 06-11-2015 15:44:33
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Lee polygone flippant
Une réflexion...
En admettant le résultat, on ne peut pas avoir de trajectoire cyclique.
Or 1 2 -3--> -2 -1 3 -->2 -3 1 --->-1 3 -2 -> 1 2 -3
Ce qui permet de conclure que le résultat est faux pour Somme = 0
(on ne pourra jamais finir à (0..0) dans ce cas sauf si on y démarre. Se montre par récurrence : si à l'étape n il y a un nombre strictement négatif, à l'étape n+1 il y aura un nombre strictement positif donc comme la somme est nulle il y aura toujours au moins un nombre strictement négatif.
Il est également faux pour Somme <0 car on a toujours au moins forcément un nombre strictement négatif donc toujours la possibilité de continuer...
Comprendre en quoi c'est différent pour Somme positive permettrait de conclure ...
On a toutefois résolu un autre problème : quand la somme est négative au sens large mais que le point de départ n'est pas (0.0..0) , on pourra toujours continuer...
#10 - 06-11-2015 18:03:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Le polygone lfippant
J'ai une solution , ça marche mais c'est vraiment tordu :
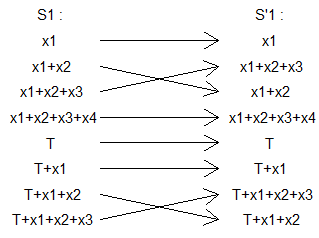
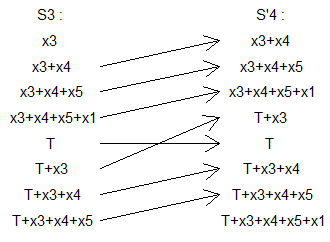
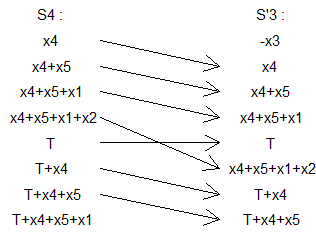
On note x1;x2;...;xn , les valeurs à chaque sommet , T la somme de ces valeurs et pour i dans [[1 ; n]] on définit :
Si={xi;xi+xi+1;xi+xi+1+xi+2;xi+xi+1+xi+2+xi+3;...}.
Les indices des xi sont pris modulo n .
Chaque Si est infini mais contient un nombre fini d'éléments négatifs ( à chaque ronde on ajoute T ) .
Maintenant que se passe-t-il sur chaque Si si on effectue l'action proposée ? On notera x′i et S′i les nouveaux et pour plus de lisibilité on supposera par exemple qu'on prend l'opposé de l'élément négatif x3 :
x′3=−x3,x′2=x2+x3,x′4=x3+x4.
Les autres xi sont inchangés : x′i=xi .
Si on détaille les éléments de S′i on obtient :
S′1=S1,S′2=S2,S′3=S4∪{−x3},S′4=S3−{x3},S′5=S5,...
L'ensemble des valeurs des Si est donc conservé , sauf x3 qui est devenu −x3 . On avait un nombre fini de valeurs négatives et on vient d'en perdre une ...
Vasimolo
#11 - 06-11-2015 18:33:29
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le polygone filppant
@nodgim: Alors c'est que je n'ai pas réussi a comprendre ce que tu décris,
Considère un cas avec un gros polygone (par exemple 12 sommets) tu as partout des 0 sauf aux deux pôles ou on trouve -1 au nord et 2 au sud. (Ces deux valeurs non nulles étant donc séparées par cinq 0 de chaque cote.) Ça donne quoi tes relations au départs? et après qq itérations?
@Vasimolo: Il y a clairement des éléments qui me font penser que tu utilises les bonnes choses. J'ai regardé vite fait mais a première vu ça me semble pas mal. Faudra juste que je vérifie que l'effet annoncé sur tes Si est bien l'effet réel. Si oui ça me semble bien marcher  bravo. C'est tordu mais ce n'est pas beaucoup plus tordu que la solution que je connais. bravo. C'est tordu mais ce n'est pas beaucoup plus tordu que la solution que je connais.
#12 - 06-11-2015 19:55:16
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Le polygone fllippant
Ah oui ça ne marche pas car il faudrait recréer des relations à chaque déplacement. Bon, l'idée ne semble pas pouvoir être prolongée...
#13 - 06-11-2015 22:19:17
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le polygone flippnt
@Vasimolo: Ta famille de Si est bien une famille d'ensembles d'entiers?
Si oui tu peux me refaire ton exemple avec des valeurs? par exemple un polygone avec un -3 quelque part et partout ailleurs des 1.
#14 - 06-11-2015 23:06:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Le polygne flippant
Les valeurs ne sont pas forcément entières 
Je veux bien développer un exemple numérique mais il cache les choses plus qu'il ne les montre .
Si on veut -3 et des 1 , il faut au moins 5 sommets . Par exemple x1=1 , x2=1 , x3=-3 , x4=1 et x5=1 alors :
S1={1;2;-1;0;1;2;3;0;1;2;3;...}
S2={1;-2;-1;0;1;2;-1;0;1;2;3;...}
S3={-3;-2;-1;0;1;-2;-1;0;1;2;-1;...}
S4={1;2;3;4;1;2;3;4;5;2;...}
S5={1;2;3;0;1;2;3;4;1;...}
Et pour les S'
S'1={1;-1;2;0;1;2;0;3;;1;2;...}
S'2={-2;1;-1;0;1;-1;2;0;1;2;...}
S'3={3;1;2;3;1;4;2;3;4;2;...}
S'4={-2;-1;0;-2;1;-1;0;1:-1;2;...}
S'5={1;2;0;3;1;2;3;1;4;2;3;...}
Il faut surtout regarder l'expression "formelle" des éléments de chaque ensemble ( le passage à l'écriture chiffrée écrase tout ) .
Vasimolo
#15 - 07-11-2015 10:02:19
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le polygone fflippant
@Vasimolo: Passer par l'expression numérique me permettait de confirmer que tu ne parles pas vraiment d'ensemble d'entiers (puisque tu gardes les homologues). Mais plutôt d'une sorte de notion d'ensemble d’écriture formelle.
Même formellement je n'arrive pas à retrouver ta relation entre S3, S4, S3' et S4' et je ne suis toujours pas sur de manipuler les bons types d'objets. Tu n'aurais pas par hasard une manière compacte et visuelle de représenter les transformation sur S3 et S4 et qui montre bien qu'on a ta relation?
Toutes mes tentatives ont données des trucs qui marchottent au départ et ne correspondent plus après 1 tour.
#16 - 07-11-2015 11:55:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Le polyggone flippant
J'ai trouvé un moyen d'illustrer mais ça va être un peu long .
Je fais ça dans la journée 
Vasimolo
#17 - 07-11-2015 12:23:26
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le polygone flipppant
C'est le moment de donner un nouvel indice!
Deuxième indice (indice moyen):
Spoiler : [Afficher le message] Sommes partielles
#18 - 07-11-2015 12:53:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#19 - 07-11-2015 15:12:20
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le polygone flippan
@Vasimolo: Oui parfait c'est validé!
Si tu t'ennuies: sur un pentagone, dans le pire cas, il faut combien d’opération?
#20 - 08-11-2015 12:44:33
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le polygone flppant
3eme indice (gros indice):
Spoiler : [Afficher le message] Prendre un sommet de référence sur le polygone, et regarder la suite des sommes partielles depuis ce sommet dans le sens de parcourt de votre choix.
#21 - 09-11-2015 23:48:43
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
L epolygone flippant
On certes une inversion des sommes de rang n-1 et n quand on modifie le sommet n ce qui montre bien d'ailleurs le nombre de limité de combinaison possibles à partir d'un point de départ...mais qui ne me permet pas de conclure...
#22 - 10-11-2015 09:36:41
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le polygone flippnat
@portugal: Regarde bien ce que cette inversion fait sur la suite, et tu verras que ça te permet de conclure. 
#23 - 10-11-2015 10:39:24
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Le polygone flippan
Avec le dernier indice, c'est plus facile, mais pas évident pour autant...
Donc on établit une suite de sommes à partir d'un sommet 1, les autres allant jusqu'à n, v(k) étant la valeur au rang k :
s(1)= nombre du sommet=v(1)
s(k)=somme algébrique v(1) à v(k)
s(n) étant la somme totale, qui est positive et invariable.
Les valeurs négatives au rang k sont repérables par le fait que s(k) < s(k-1).
Une action en k, si v(k) < 0 , se traduit uniquement par un échange des sommes s(k) et s(k-1). Si notre suite des s(k) est établie de gauche à droite, chaque action sur cette valeur "a" qui correspond au s(k) de départ la décale vers la gauche. Comme s(n) est algébriquement positive, cette valeur "a" tombera forcément sur un s(j) plus petit que "a", qui se traduit par un s(j+1)=a > s(j), c'est à dire v(j+1)>0. Avant que "a" n'atteigne le rang s(j+1), on a s(j)<s(j+1) car "a" a pu passer s(j+1) mais pas s(j). Quand "a" vient s'insérer entre les 2 valeurs: s(j) < a < s(j+1), on a s(j+1)-s(j)=s(j+1)-a + a-s(j). C'est à dire que l'emplacement final de "a" n'augmente pas l'écart entre s(j) et s(j+1).
En revanche, si l'emplacement initial de "a" en k était suivi par un v(k+1) positif (ou nul ou moins négatif que "a"), quand le "a" se décale à droite, l'écart entre s(k-1) et s(k+1) diminue. Donc, dans ce cas, le bilan est une diminution de la somme de la valeur absolue des écarts entre s(k) voisins. Or il existe forcément des cas où "a" est suivi d'un positif (ou nul ou moins négatif que "a"): si la suite des v(k) négatives est groupée, au moins le dernier.
Donc la diminution de la somme des valeurs absolues des écarts associée aux actions est inexorable. Et donc aussi la disparition des valeurs négatives.
#24 - 10-11-2015 11:47:14
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
#25 - 10-11-2015 16:04:52
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le polygone fliippant
Ajout de la solution dans le post initial.
Merci à tous les participants!
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum