 |
#1 - 03-08-2021 17:59:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
yn simple polygone
Bonjour à tous 
Cela aurait pu être un gâteau si j'en avais gardé le goût .
On considère un polygone simple dont les sommets sont aux nœuds d'un réseau hexagonal régulier de maille 1 cm² et dont tous les angles sont des multiples de 60° . Construire ce polygone sachant que son aire vaut 45,5 cm² , qu’il y a 9 points du réseau sur sa frontière et 89 à l’intérieur .
Amusez-vous bien 
Vasimolo
#2 - 05-08-2021 10:12:59
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Un simlpe polygone
Ca faisait un moment que je me demandais s'il y avait un équivalent au théorème de Pick sur un maillage hexagonal... Je vais y réfléchir tiens 
#3 - 05-08-2021 10:55:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Un simpe polygone
C'est une bonne idée Scarta mais tu verras très vite que cette formule s'adapte assez mal au réseau hexagonal . C'est pourtant dans ce sens qu'il faut chercher l'unique solution ( à une isométrie près ) .
Vasimolo
#4 - 05-08-2021 11:58:30
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Un ssimple polygone
C'est ce que je me suis dit aussi. Si on transforme le maillage orthogonal en maillage triangulaire, à mon avis on peut adapter la formule de Pick, avec l'ajout d'un facteur sqrt(3)/2, qui est l'unité de mesure du "petit carré" qui devient un "petit parallélogramme".
Par contre, c'est bizarre : ce maillage triangulaire contient le maillage hexagonal, si je ne m'abuse. On aurait donc juste des points en plus par rapport aux 9 / 89 annoncés si on se mettait sur un maillage triangulaire. Et arriver à un résultat rationnel... j'ai du rater un truc 
#5 - 05-08-2021 12:14:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un simple poltgone
Tu progresses à grands pas , disons que les "trous" ne sont pas régulièrement répartis à l'intérieur du polygone .
Vasimolo
#6 - 05-08-2021 15:30:22
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Un simple polyogne
Oui ça je veux bien, mais c'est étrange. Supposons un polygone sur un maillage hexagonal, rajoutons les points qui manquent pour faire un maille triangulaire
> Ces points existent bien
> Le polygone est toujours sur le maillage
> Les nouveaux points sont soit dans le polygone, soit en dehors, soit sur la bordure ==> mes nombres 9 et 89 évoluent, on leur ajoute un nombre entier de points pour chacun.
D'après la formule précédente dérivée de Pick, je peux calculer son aire, elle sera "un entier" * sqrt(3)/4. Pour en faire 45,5...
A moins bien sur que 45.5 ne soit qu'une approximation (on aurait alors 2i+b = 107 et une aire de de 45,46633 environ), mais j'ai été habitué à plus de rigueur ici ! 
#7 - 05-08-2021 17:10:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un qimple polygone
Non , l'aire donnée est exacte ( pas d'approximation ) .
Oublie un peu ton coefficient et donne explicitement ta formule dans le réseau que tu as choisi ( tu peux choisir comme unité d'aire celle de la cellule de base de ton maillage ) . Après il faudra repérer les points à évacuer .
Vasimolo
#8 - 07-08-2021 20:17:59
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Un simple polygne
Salut 
J'ai trouvé celui-ci qui correspond:
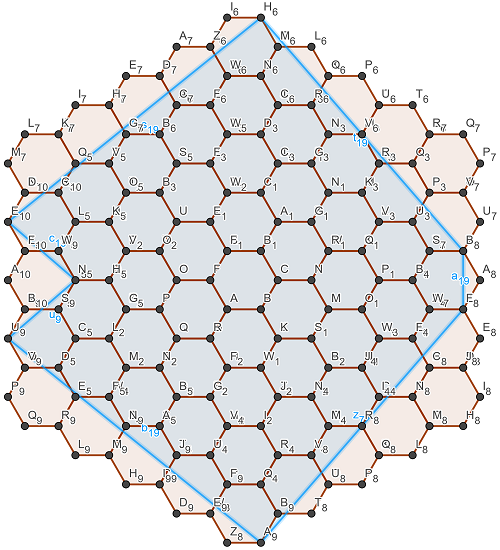
Les nœuds V6 et R8 sont sur la frontière.
Les nœuds E5 et Q5 sont (tout juste) en dehors.
#9 - 07-08-2021 22:09:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un simplr polygone
Bonjour Sydre , c'est bien essayé mais il manque la condition sur les angles . Il est très difficile de trouver l'unique solution par tâtonnement . Le mieux serait de trouver une façon de construire le polygone mais ce n'est pas facile non plus 
Vasimolo
#10 - 11-08-2021 18:59:02
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Un simple polyygone
il manque la condition sur les angles
C'est tout de suite moins simple 
Es-tu certain qu'il est unique cependant? J'arrive à un résultat contraire.
Mon ébauche de réflexion:
On peut montrer que les cotés d'un tel polygone sont tous multiples de son plus petit segment (segments = cotés en prenant en compte les sommets "dégénérés" avec un angle de 180°).
Il en résulte que le polygone est triangulable par un réseau régulier de triangles équilatéraux ayant pour maille le triangle équilatéral de coté le plus petit segment du polygone.
On a donc la relation i_p+f_p=n\cdot i_m+f_t, avec:
- i_p le nombre de nœuds du réseau hexagonal contenus dans le polygone
- f_p le nombre de nœuds du réseau hexagonal sur la frontière du polygone
- n le nombre de mailles triangulaires constituant le polygone
- i_m le nombre de nœuds du réseau hexagonal contenus dans une maille triangulaire
- f_t le nombre de nœuds du réseau hexagonal sur la frontière de la triangulation
On cherche une solution unique telle que i_p=89 et f_p=9
On peut toujours assembler un nombre de maille triangulaire n>3 de plusieurs façons différentes donc n\leq 3
Or pour n<6 on montre que f_p=f_t=2+n et donc i_p=n\cdot i_m
Problème: impossible par conséquent d'avoir à la fois f_p=9 et l'unicité de la solution ...
#11 - 11-08-2021 19:31:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un simple polygobe
Je n'ai pas tout analysé mais à priori , il y a quelques imprécisions :
1°) Le polygone peut être décomposé en triangles équilatéraux identiques , d'accord mais les trois sommets ne sont pas toujours sur le réseau .
2°) Chaque triangle de base ne contient pas forcément le même nombre de points du réseau .
Jusqu'à preuve du contraire la solution reste unique mais quelle est-elle ?
Vasimolo
#12 - 12-08-2021 07:56:02
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Un simpe polygone
Salut,
Un petit indice pour orienter les recherches ?
Les côtés du polygone sont-ils parallèles à ceux de la trame hexagonale ?
Ou y a t-il un décalage angulaire entre les deux ?
Merci et bonne journée.
#13 - 12-08-2021 09:56:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Un imple polygone
Je ne vais pas donner d'indice mais relever deux bonnes idées :
Scarta a pensé à la formule de Pick : très bien .
Sydre a pensé à décomposer la figure en triangles équilatéraux identiques : très bien .
Amusez-vous bien , la recherche est vraiment réjouissante 
Vasimolo
#14 - 14-08-2021 11:13:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un simple pomygone
Je n’ai pas trop envie de dévoiler la solution , je précise simplement quelques détails techniques pour vous permettre de continuer à chercher sans vous embarrasser de calculs laborieux .
La formule de Pick s’adapte sans problème à un réseau triangulaire :
A = F+2I-2 ( l’unité d’aire étant fournie par le triangle ) .
Avec l’unité choisie ici : 6A=F+2I-2 .
Une bonne idée pour commencer : compléter la grille en un maillage triangulaire .
Amusez-vous bien 
Vasimolo
#15 - 16-08-2021 09:25:54
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Un smiple polygone
ok, je viens de réaliser que chaque maille fait 1cm2, et pas 1cm de côté 
Du coup, je comprends mieux pourquoi ce problème est possible...
J'ai la tête dans coaltar, je verrais si j'arrive à continuer dessus.
#16 - 18-08-2021 12:15:32
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
un simpke polygone
(un peu plus tard...)
Je suis arrivé à la conclusion qu'il n'y a pas de formule de Pick simple pour un maillage hexagonal, en tout cas pas aussi simple que pour les maillages triangulaires / orthogonaux.
On peut très facilement dessiner deux triangles, dont les sommets sont des noeuds, et qui ne contiennent aucun autre point en intérieur ou en bordure, et dont les aires seront pourtant différentes. Ex: un triangle qui prend 3 sommets consécutifs d'un hexagone vs un triangle qui prend un sommet sur deux sur le même hexagone.
J'ai l'impression que la condition sur les angles nous place dans un cas particulier et que dans ce cas précis, on pourrait sortir une formule qui ne marcherait pas pour tous les polygones.
#17 - 18-08-2021 14:49:48
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Un siple polygone
Salut,
Pour ma part, j'ai essayé de raisonner (sans succès jusqu'à présent) sur une maille de triangles équilatéraux, créée en rajoutant un point au centre de chaque hexagone. Mais ces points "fictifs" semblent semer la zizanie.
Affaire à suivre ...
#18 - 18-08-2021 16:58:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un sumple polygone
Tout ce qui a été dit est juste , même s'il gène un peu le réseau triangulaire est utile . Il y a tout de même quelque chose d'important qui a été oublié : le polygone peut être pavé avec des triangles équilatéraux de même taille dont les sommets sont aux nœuds du réseau triangulaire .
Vasimolo
#19 - 25-08-2021 13:39:45
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 78
Un smiple polygone
Bonjour tout le monde,
Un polygone composé de 7 triangles :
avec 5*13+12*2 = 89 pour les points intérieures et 9 points sur la frontière
surface d'un triangle = ( 3+2*19points intérieurs sur le réseau triangulaire -2) = 39 petits triangles
surface du polygone = 7*39 = 273 petits triangles= 45,5 hexagones
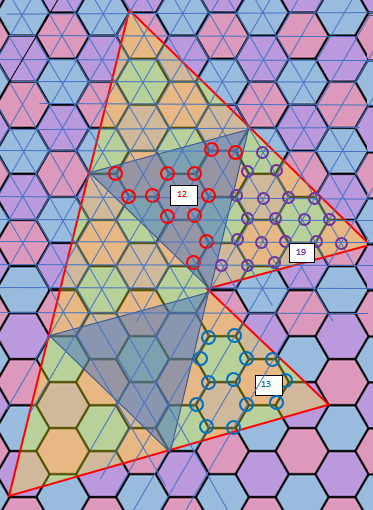
Je suis parti de la décomposition 273=3*7*13 et ensuite tâtonné pour trouver les 7 triangles avec les 19 points intérieurs sur le réseau triangulaire
Ce qui une fois le problème posé n'est pas si long ,le début fut plus laborieux !
Le nombre de points intérieurs a déterminé qu'il fallait 2 triangles "bleus" et 5 "jaunes" ( et non le contraire)
#20 - 25-08-2021 18:10:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un qimple polygone
C'est ça LeJeu , bien vu 
On peut s'amuser à montrer que la solution est unique mais c'est une autre paire de manches 
Vasimolo
#21 - 25-08-2021 20:57:56
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 78
Un simple ploygone
Bonsoir Vasimolo
Merci pour ce challenge, et pour le gros coup de pouce en donnant la formule de Pick sur un réseau triangulaire ( il faut que je regarde si j'arrive bien à la prouver.)
Sinon, je me suis servi dans mes tâtonnements de ton dernier indice le polygone peut être pavé avec des triangles équilatéraux de même taille dont les sommets sont aux nœuds du réseau triangulaire
En fait, l'affirmation ne me semble pas si évidente .. tu détaillerais s'il te plait ?
Le Jeu
#22 - 26-08-2021 09:40:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un simple poltgone
En fait l’explication est assez simple 
On considère deux points du réseau triangulaire qui se suivent sur la frontière du polygone . On peut choisir ces points pour que la longueur L du segment qu’ils bornent soit minimale . Ce segment génère un unique réseau triangulaire contenu dans le premier . Comme les angles du polygone sont des multiples de 60° , ses côtés vont suivre ceux du deuxième réseau et les longueurs des côtés vont être multiples de L . On peut donc paver l’intérieur du polygone avec des triangles équilatéraux de côté L . Il faut tout de même faire attention , les sommets des triangles ne sont pas nécessairement des points du réseau hexagonal . Disons qu’il y a deux cas , soit tous les triangles ont deux sommets sur le réseau hexagonal , soit ils ont tous leurs sommets sur le réseau .
Vasimolo
#23 - 26-08-2021 09:53:01
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Un smiple polygone
Ah oui. J'avais moi aussi buggé sur l'assertion (enfin surtout sur la partie "de même taille"), mais c'est vrai qu'en changeant de maillage c'est trivial :p
#24 - 30-03-2022 11:31:22
- shemzy
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 2
Un simpl epolygone
Ca faisait un moment que je me demandais s'il y avait un équivalent au théorème de Pick sur un maillage hexagonal... Je vais y réfléchir tiens smile
_____________________________________________
Veterinary Suction Unit
#25 - 30-03-2022 13:56:38
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
un simpme polygone
c'est marrant j'aurais pu dire la même phrase... ah ben en fait je l'ai dite 
|
 |

 Accueil
Accueil
 Forum
Forum








