Oyez, oyez, la mystérieuse histoire de Jean-Claude, l'abeille mathématicienne.
Jean-Claude l'abeille doit se rendre à une alvéole afin de nourrir une larve. Il se déplace d'alvéole en alvéole. La distance entre deux alvéoles est, par définition, la distance entre leurs deux centres, et on pose à 1 la distance entre deux alvéoles qui se touchent.
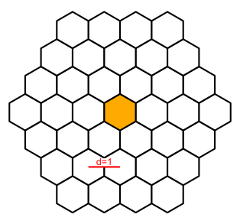
D'un côté, Jean-Claude souhaite prendre le maximum de temps possible pour effectuer sa tâche, afin de réfléchir en chemin à la démonstration de la conjecture de Riemann. D'un autre côté, il doit prendre garde à ne pas être identifié comme un tire-au-flanc, sinon il risque de se retrouver affecté à la surveillance de la ruche face à vespa velutina, activité périlleuse si elle en est.
Jean-Claude décide ainsi de se fier aux deux règles suivantes :
* règle 1 (prudence) : à chaque déplacement, il se rapproche strictement de son but, pour ne pas se faire repérer.
* règle 2 (nonchalance) : il emprunte un trajet le plus long possible pour rejoindre son but.
On sait de plus que la trajectoire empruntée ne comporte pas d'angle aigu (sur la figure ci-dessous, la trajectoire de droite comporte un angle aigu, pas celle de gauche), et qu'initialement, la distance entre Jean-Claude et la larve est un nombre premier.
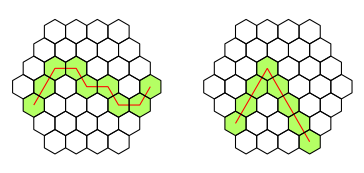
Pouvez-vous déterminer quelle est la longueur du plus grand trajet qui vérifie les conditions de l'énoncé ?
Indice 1 :
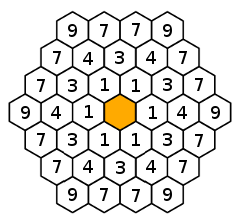
Spoiler : [Afficher le message] Il peut être utile de calculer les distances des cellules de la ruche à la larve. L'image ci-dessous donne les carrés de ces distances :
Indice 2 :
Spoiler : [Afficher le message] Si Jean-Claude est placé initialement dans une cellule à la distance 3 de la larve (donc numérotée 9 dans le dessin de l'indice 1), l'application des règles 1 et 2 implique qu'il va suivre le chemin 9-7-4-3-1-0 (chemin de longueur 5).
Or un tel chemin comporte forcément au moins un angle aigu (9-7-4). On en déduit que Jean-Claude n'est initialement pas placé sur cette cellule.
Indice 3 :
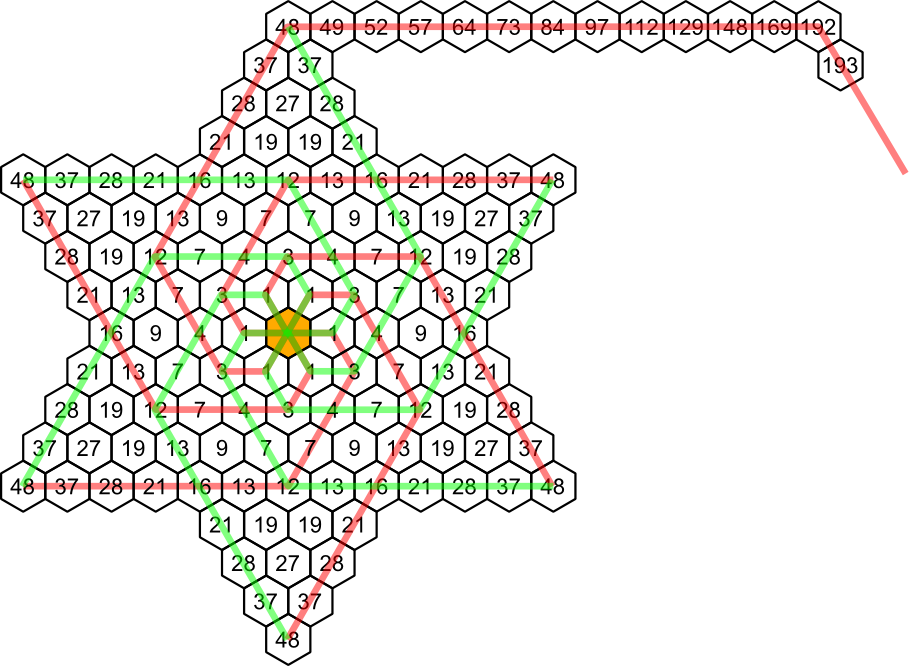
Spoiler : [Afficher le message]
S'il respecte les deux règles, et si sa trajectoire ne comporte pas d'angle aigu, alors Jean-Claude emprunte une des spirales rouges et vertes :

 Accueil
Accueil
 Forum
Forum










