Bonjour à tous,
je suis en train de refaire ma salle de bain. Je dispose de carreaux de trois sortes, présentés ci-dessous ; et j'aimerais, à l'aide de ces carreaux, représenter les quatre noeuds non triviaux les plus simples.
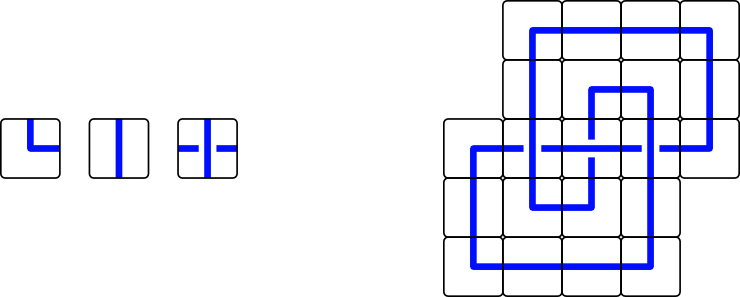
De combien de carreaux au minimum ai-je besoin pour chacun de ces noeuds ?
Voici une table donnant les quatre noeuds non triviaux (le noeud trivial est un simple cercle) les plus simples, ce sont ceux nécessitant 5 croisements ou moins :
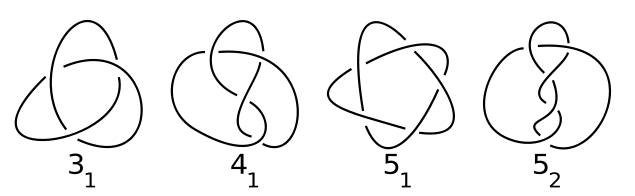
J'ai donné un exemple pour le noeud de trèfle (le noeud 31) qui nécessite 21 carreaux. Peut-être pouvez-vous trouver mieux ?
Addendum : cette énigme vous fera travailler avec les noeuds (https://fr.wikipedia.org/wiki/N%C5%93ud … atiques%29). On peut visualiser un noeud en prenant une ficelle, en la faisant se contorsionner, puis en collant les extrémités. Si alors, on déplace la ficelle sans décoller les extrémités, cela reste le même noeud. Ce faisant, le noeud change de forme ; on peut même rajouter des croisements inutiles, tant qu'on ne coupe pas la ficelle, cela reste le même noeud. En particulier, le noeud réalisé en bleu dans mon exemple est bien le noeud de trèfle 31 , mais ce n'est pas immédiat, il faut prendre un crayon et une gomme pour s'en convaincre (ou mieux, une ficelle).
P.S. : cette énigme ne nécessite aucune connaissance particulière en théorie des noeuds, tout le monde peut s'y essayer. Mais la résoudre parfaitement demandera un peu d'astuce. Par ailleurs, je n'ai pas cherché à prouver que mes solutions étaient optimales, aussi il n'est pas impossible que vous trouviez de meilleures solutions que moi.

 Accueil
Accueil
 Forum
Forum








