 |
#1 - 08-03-2017 22:00:45
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Décoration de salle de baiin
Bonjour à tous,
je suis en train de refaire ma salle de bain. Je dispose de carreaux de trois sortes, présentés ci-dessous ; et j'aimerais, à l'aide de ces carreaux, représenter les quatre noeuds non triviaux les plus simples.
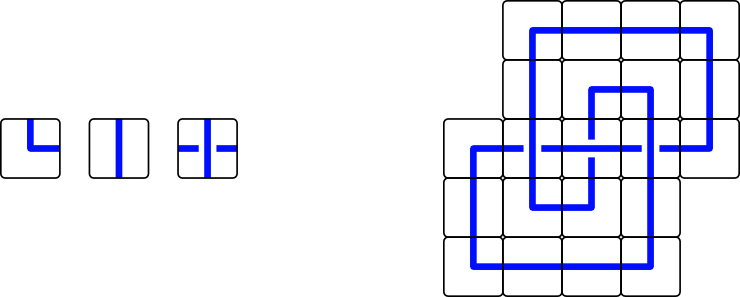
De combien de carreaux au minimum ai-je besoin pour chacun de ces noeuds ?
Voici une table donnant les quatre noeuds non triviaux (le noeud trivial est un simple cercle) les plus simples, ce sont ceux nécessitant 5 croisements ou moins :
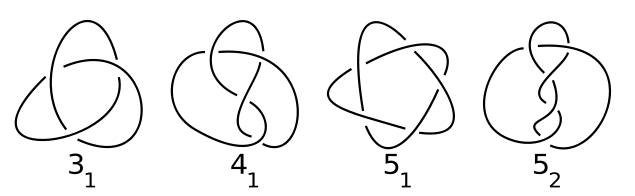
J'ai donné un exemple pour le noeud de trèfle (le noeud 31) qui nécessite 21 carreaux. Peut-être pouvez-vous trouver mieux ?
Addendum : cette énigme vous fera travailler avec les noeuds (https://fr.wikipedia.org/wiki/N%C5%93ud … atiques%29). On peut visualiser un noeud en prenant une ficelle, en la faisant se contorsionner, puis en collant les extrémités. Si alors, on déplace la ficelle sans décoller les extrémités, cela reste le même noeud. Ce faisant, le noeud change de forme ; on peut même rajouter des croisements inutiles, tant qu'on ne coupe pas la ficelle, cela reste le même noeud. En particulier, le noeud réalisé en bleu dans mon exemple est bien le noeud de trèfle 31 , mais ce n'est pas immédiat, il faut prendre un crayon et une gomme pour s'en convaincre (ou mieux, une ficelle).
P.S. : cette énigme ne nécessite aucune connaissance particulière en théorie des noeuds, tout le monde peut s'y essayer. Mais la résoudre parfaitement demandera un peu d'astuce. Par ailleurs, je n'ai pas cherché à prouver que mes solutions étaient optimales, aussi il n'est pas impossible que vous trouviez de meilleures solutions que moi.
#2 - 08-03-2017 23:36:13
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Décoration de saalle de bain
P.S. : cette énigme ne nécessite aucune connaissance particulière,
Euh, comprendre l'énoncé, c'est une compétence particulière ?
j'aimerais, à l'aide de ces carreaux, représenter les quatre noeuds non triviaux les plus simples (ceux nécessitant 5 croisements ou moins).
Ton bidule en trèfle, il ne fait pas partie du lot ? (juste 3 croisements)
Alors on les cherche où (sans connaissance) les figures à 5 croisements ?
#3 - 09-03-2017 00:09:17
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Décoration de salle de bin
@gwen27 : j'ai mis l'énoncé à jour, est-ce plus clair ainsi ?
Le noeud de trèfle fait partie du lot : 3 croisements, ça fait bien 5 croisements ou moins. Les 4 noeuds à réaliser en carrelage sont bien ceux donnés dans l'énoncé (31, 41, 51 et 52 sont leurs petits noms).
#4 - 09-03-2017 16:00:52
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Dcéoration de salle de bain
Bonjour,
Voila mes solutions pour les deux premiers
le premier nœud en 13 dalles:
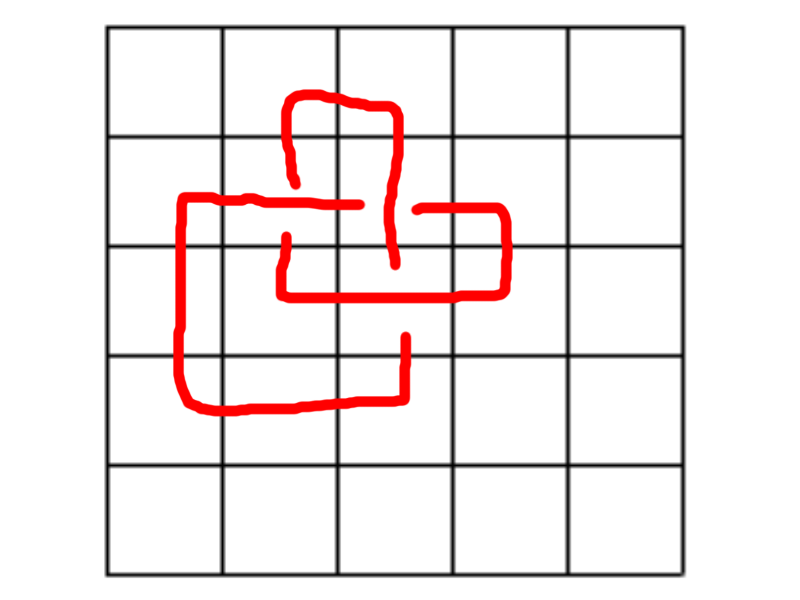
Le deuxième nœud en 17 dalles:
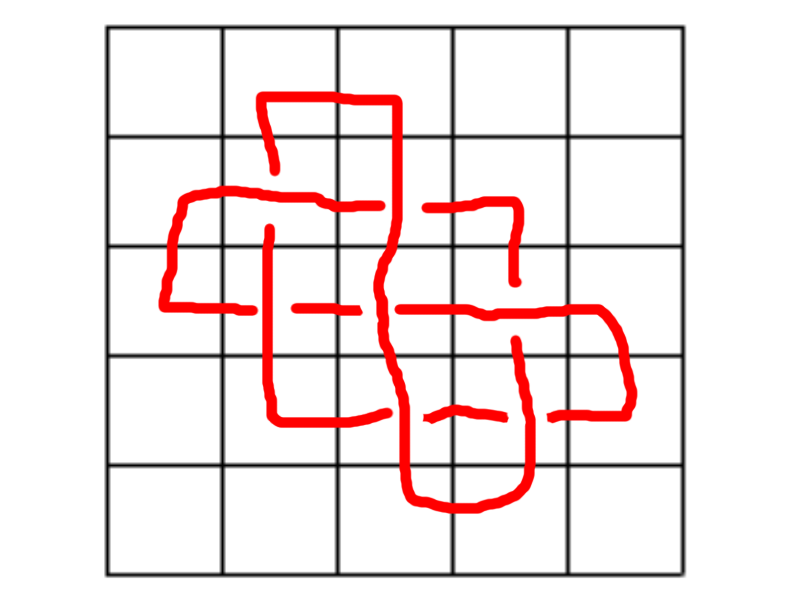
Une petite démonstration de l'optimalité pour le premier nœud:
quelques propriétés:
(1)chaque croisement possède 4 voisins
(2)chaque dalle possède minimum 2 voisins
(3)un circuit passe par un nombre pair d'étapes (si on dame le quadrillage en noir et blanc, chaque déplacement change de couleur de case, il faut un nombre pair de déplacements pour revenir sur sa couleur.
Ici, il y a au moins trois croisement. Si on les place en angle, d'après (1), on a minimum 10 dalles. En utilisant (2), on en a minimum 12.
Supposons qu'il y ait exactement trois croisements. Alors le nombre de dalles utilisées est impair d'après (3) (3 croisements, donc dalles ou on passe deux fois, donc nbr de dalles + nbr de croisements = nbr de déplacement) donc le minimum est 13.
Si il y en a 4, si on veut rester sur 12 cases, le 4 croisement termine le carré formé avec 3 autres.
Le dessin forme alors un carré de 4 dalles entourés de 8 dalles. Si on entre dans un croisement, on passe forcément par celui aligné. Si on relie de la seule manière possible, on trouve deux fils non reliés, donc pas de nœud. donc le minimum est donc 13.
Pour le deuxième nœud, ça m'a l'air beaucoup plus laborieux
Edit
Bon, j'ai pas trop cherché plus, mais pour les deux derniers, je trouve chacun 19:
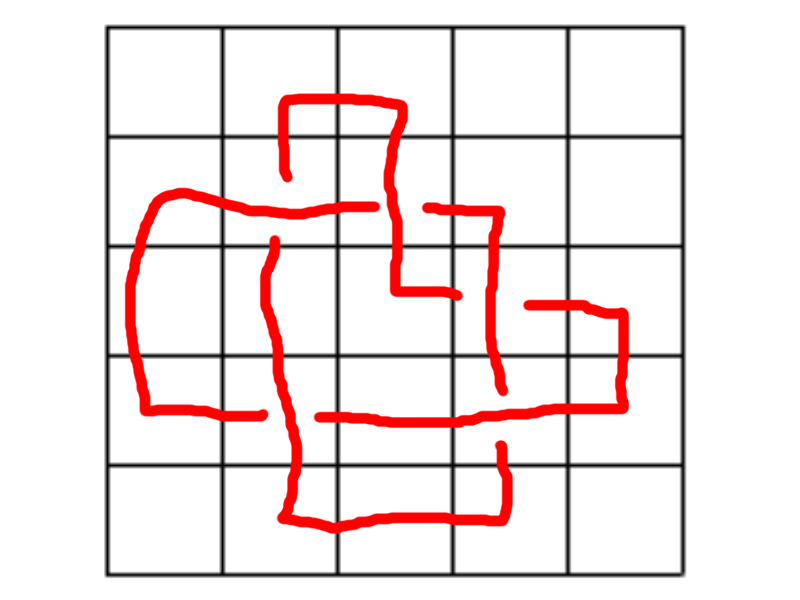
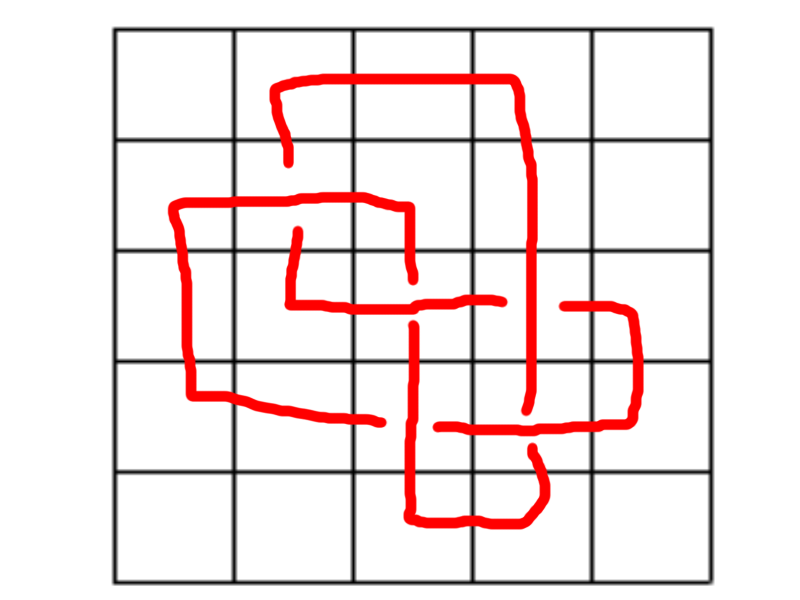
On peut démontrer très facilement pour ces deux là que l'on ne peut pas faire mieux que 17, exactement de la même manière. (A savoir qu'en fait, le cas 6 croisements (tout comme le cas 4 croisements pour le 1er noeud) n'a pas besoin d'être traité car si on trace le graphe formé par la ficelle (avec pour sommets les croisements de base) il est planaire, et si on crée un nouveau croisement, on entre dans une face, de laquelle il faudra sortir, donc minimum 2 croisements en plus...
Pour monter à 19, c'est un peu plus chaud...
#5 - 09-03-2017 16:46:12
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Décration de salle de bain
Salut,
Je propose un nœud 3(1) avec 13 carreaux
ainsi qu'un ... faux nœud
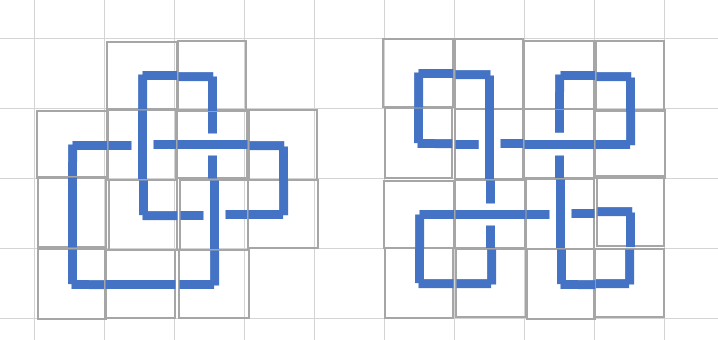
voici un vrai nœud 4(1) avec 17 carreaux, les images à droite montrent le même nœud démêlé, le plus à droite est identique à l'exemple.
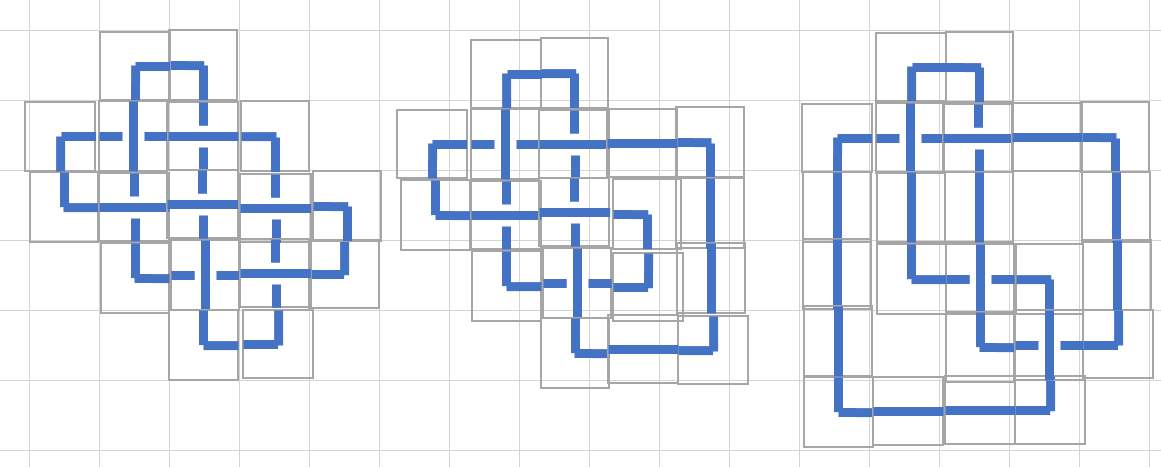
Merci
The proof of the pudding is in the eating.
#6 - 09-03-2017 20:01:09
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Décoratio nde salle de bain
@caduk : bravo pour ta démo de l'optimalité de ta solution pour le premier noeud !
J'ai trouvé les mêmes solutions que toi, sauf pour 52 où j'ai réussi à faire mieux.
@franck9525 : très bien ! tu as trouvé les meilleurs résultats pour les deux premiers noeuds.
#7 - 09-03-2017 20:35:48
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Dcoration de salle de bain
Effectivement, on trouve 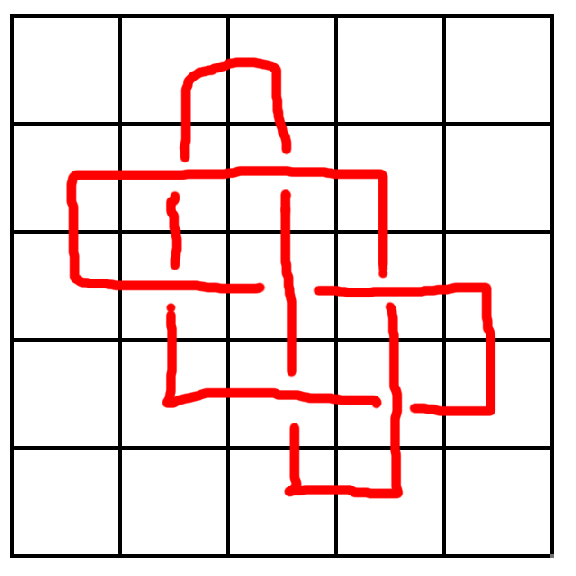 qui est donc solution optimale. Avec ce schéma à 7 croisements, il est malheureusement impossible de l'adapter pour le premier. Un début de preuve pour 5.1? qui est donc solution optimale. Avec ce schéma à 7 croisements, il est malheureusement impossible de l'adapter pour le premier. Un début de preuve pour 5.1?
#8 - 09-03-2017 21:45:42
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Décoraiton de salle de bain
#9 - 10-03-2017 12:43:25
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Décoration de salle de baiin
Bonjour,
Si j'ai bien compris, (maintenant), je trouve 13 pour 3 noeuds, 19 pour 5 noeuds et bizarrement, je ne trouve pas mieux que 20 pour 4 noeuds...

#10 - 10-03-2017 17:50:47
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Décoration de salle dde bain
@gwen27 : très jolis dessins, très clairs ! C'est bon pour 31 et 51, mais de manière surprenante, on peut faire mieux pour 41 et 52. Pour cela, il y a une certaine astuce pas évidente à imaginer...
#11 - 11-03-2017 08:30:36
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Décoration de salle de ban
Je ne trouve pas mieux pour 5-2 , il faut surement faire un faux croisement quelque part...
Par contre j'ai un truc rigolo avec 4-1, on doit toujours pouvoir faire au moins aussi bien avec 4-1 qu'avec 5-2:

Et une petite amélioration de l'un avec 2 faux croisements (et donc de l'autre ) ce qui donne 17 :

#12 - 11-03-2017 16:13:01
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Décorationn de salle de bain
#13 - 12-03-2017 12:14:08
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Décoration de salle de bbain
Merci et félicitations aux participants. La subtilité de l'énigme, c'est que pour trouver la solution optimale de 41 ou 52, il faut recourir à des croisements inutiles, ce qui est assez surprenant.
#14 - 12-03-2017 14:45:38
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Décoration dde salle de bain
Pour le 4, j'ai finalement réussi à le démontrer, mais je ne posterai pas la démonstration dans le détail parce que c'est beaucoup d'études de cas.
On peut remarquer qu'il suffit de démontrer le résultat pour seulement 4 croisements, car sinon, il faut minimum 6 croisements, et on a démontré qu'à partir de 5 croisements, on ne pouvait pas faire mieux que 17.
Ici, ┼ désigne un croisement, o une dalle avec seulement deux extrémités, * une dalle à déterminer(pas un croisement),
On peut essayer de trouver quelques propriétés:
1)On ne peut pas avoir une boucle de 4 cases avec un croisement au début de la boucle (sinon, le nœud peut se simplifier en déroulant cette boucle (voir le "faux nœud" de franck, chacune des extrémités est une boucle qui peut être déroulée, et au final, on a pas le nœud 4) Cette propriété fonctionne car on étudie le cas 4 croisements, donc chaque croisement est essentiel dans le nœud.
2)le shéma
┼*┼
se simplifie en:
┼─┼
3)le schéma:
┼*┼
*┼*
est impossible
4)le schéma
┼*
┼
se simplifie en:
┼┐
┼
etc...
A partir de là, on étudiant chaque configuration de 4 croisements telle que l'application des 3 propriétés de mon premier message reste inférieure à 17, on peut utiliser ces propriétés pour construire les "chemins" surement suivis par la ficelle.
Ensuite, une très courte étude de cas suffit à montrer que si l'on cherche à relier les différents bouts de manière à obtenir un chemin continu passant partout, on ne parvient jamais à le faire en moins de 17 coups. Il n'y a pas tant de cas à analyser que ça, et grâce à ces propriétés, l'étude va très vite...
il ne reste donc plus que le nœud 5.1, ça doit pouvoir se faire de la même manière, mais en un peu plus long (grosso modo, faut tester toute les pièces du jeu blokus, plus les possibilités qui sont reliées par un coin, et 1 ou 2 pas reliées du tout... et ça en fait pas mal!
Sinon, il faut trouver une autre méthode, j'avais tenté un peu de théorie des graphes, mais ça n'a pas donné grand chose...
des prétendants pour les 3 nœuds à 6 croisements?
|
 |

 Accueil
Accueil
 Forum
Forum















 qui est donc solution optimale. Avec ce schéma à 7 croisements, il est malheureusement impossible de l'adapter pour le premier. Un début de preuve pour 5.1?
qui est donc solution optimale. Avec ce schéma à 7 croisements, il est malheureusement impossible de l'adapter pour le premier. Un début de preuve pour 5.1?