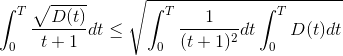Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 29-05-2015 19:53:49
L'heur du bainUn robinet de débit volumique D(t) USI déverse de l'eau dans une baignoire sans jamais la faire déborder.
#0 Pub#2 - 29-05-2015 23:23:11
L'heuer du bainil suffit que, sur une durée suffisamment longue, D(t)^(1/2)/(t+1) > D(t), soit D(t)<(1/(t+1))². #3 - 29-05-2015 23:34:33#4 - 30-05-2015 00:57:59#5 - 30-05-2015 03:38:06
l'heure du baonSi j'ai bien compris ta question on doit montrer s'il y a un cas où le volume à l'intérieur de la baignoire tend vers l'infini. #6 - 30-05-2015 13:13:31#7 - 30-05-2015 15:09:40#8 - 30-05-2015 15:46:07#9 - 30-05-2015 16:08:02
L'heure du baiPS:J'ai écrit ce message avant de lire ton dernier message. #10 - 30-05-2015 16:23:32
l'geure du bainPour répondre à ton dernier message. #11 - 30-05-2015 17:27:57#12 - 30-05-2015 17:59:35
L'heure du ainLa ça devient étrange on a par exemple: #13 - 30-05-2015 19:24:47#14 - 31-05-2015 02:30:57
L'eure du bainOn pose: #15 - 31-05-2015 15:09:06#16 - 31-05-2015 17:47:57
l'heire du bainIl faut chercher toutes les fonctions D telles que l'intégrale de 0 à l'infini par rapport au temps est convergente pour avoir un baignoire qui ne déborde pas. "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #17 - 31-05-2015 17:58:01#18 - 01-06-2015 23:12:58
L'heurre du bainPeu de participants mais voilà la solution #19 - 02-06-2015 00:00:00#20 - 02-06-2015 22:28:13
LL'heure du bainArf, je n'avais pas compris la question. Je pensais que la baignoire n'était pas bouchée dans le fond. Mais même si j'avais compris, je n'aurais jamais trouvé. Cauchy-Schwarz, c'est très très loin, et ça a du représenter 5 minutes de toute ma scolarité #21 - 03-06-2015 08:36:37
L'heure du bianPour moi pareil, je voyais une baignoire avec un trop plein... Réponse rapideSujets similaires
|
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.





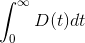 converge déterminer la nature de l'intégrale
converge déterminer la nature de l'intégrale 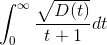
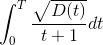 est le produit scalaire de
est le produit scalaire de 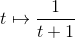 et
et 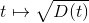 et on peut donc appliquer l'inégalité de Cauchy-Schwarz :
et on peut donc appliquer l'inégalité de Cauchy-Schwarz :