Bjr à tous 
Spoiler : [Afficher le message] OP=2, M milieu de OP => OM=MQ=1 cm
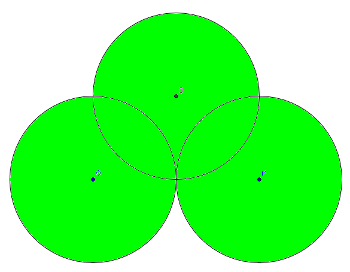
Appelons (C1) le cercle de centre O, (C2) le cercle de centre P, et (C3) le cercle de centre Q.
les cercles (C1) et (C3) se croisent en deux points : M et R,
R appartenant à (C1) et (C3), on a OR=QR=1 cm
les points M et Q sont sur la médiatrice de OP, donc OP┴MQ
M est milieu de OP, donc on a aussi OM┴MQ
OM=MQ=QR=OR=1, et OM┴MQ
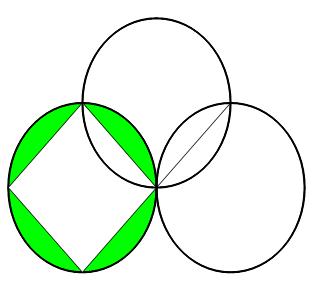
=> (OMQR) est un carré de côté 1cm, de surface 1*1=1cm²
On note A l'intersection de (C1) avec (OQ), et B l'intersection de (C3) avec (OQ)
Le quart de cercle de centre O, passant par M, A et R
a pour surface 1/4.π.1²=π/4 cm²
Si on retire la surface du quart de cercle au carré (OMQR),
il reste une surface de 1-π/4 cm²
Par construction, il y a une symétrie axiale (MR), le quart de cercle de centre Q, passant par M, B et R a également pour surface π/4 cm²
Là encore, si on retire la surface du quart de cercle au carré (OMQR),
il reste une surface de 1-π/4 cm²
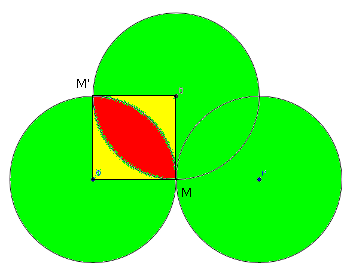
La "lentille", (MARB) d'axe (MR), colorée en rose, a pour surface 1-2*(1-π/4)=π/2-1
Le même raisonnement peut s'appliquer pour le cercle (C2), où l'on obtiendra une deuxième lentille de même surface π/2-1
Finalement, la zone recherchée a pour surface la somme des surfaces des trois cercles, diminuée des deux lentilles,
soit 3*π*1²-2*(π/2-1)=2π+2 ~8.2832 cm²


 Accueil
Accueil
 Forum
Forum