Je vous soumets ce petit problème issu d'une mésaventure qui m'est arrivée dernièrement.
Dans un temps fort fort lointain, j'avais fait choix pour tapisser une chambre d'enfant, d'un papier peint vendu comme "lavable, non stripable".
Je n'ai pas regretté mon choix quand il s'est agi d'effacer les gribouillis des petits monstres et j'ai aussi apprécier plus tard sa très bonne tenue dans le temps.
Mais, ce fut une autre affaire quand, les enfants ayant quitté le nid familial, j'ai voulu le décoller pour changer la déco.
La première couche était effectivement parfaitement étanche et a résisté aussi bien au produit de décollage qu'à la vapeur d'eau bouillante.
Il me restait donc qu'à attaquer cette première couche à la spatule, en décollant un petit coin et en tirant précautionneusement de manière à enlever un morceau le plus grand possible.
Il m'a fallu deux jours pour arriver à bout de cette tâche : si parfois, j'arrivais à décoller un morceau supérieur à un dm², la plupart du temps cela se chiffrait en dizaines de cm², et pour le plus petit, à à peine plus de 2 cm² !
J'évalue finalement à environ 14000 (1) le nombre de morceaux arrachés pour venir à bout des 28 m² (1) de papier peint de cette chambre.
Compte tenu de la disparité aléatoire des surfaces et du nombre de morceaux obtenu, on peut raisonnablement penser que ces surfaces sont réparties suivant une courbe de Gauss (2) (Merci Klim  ):
):
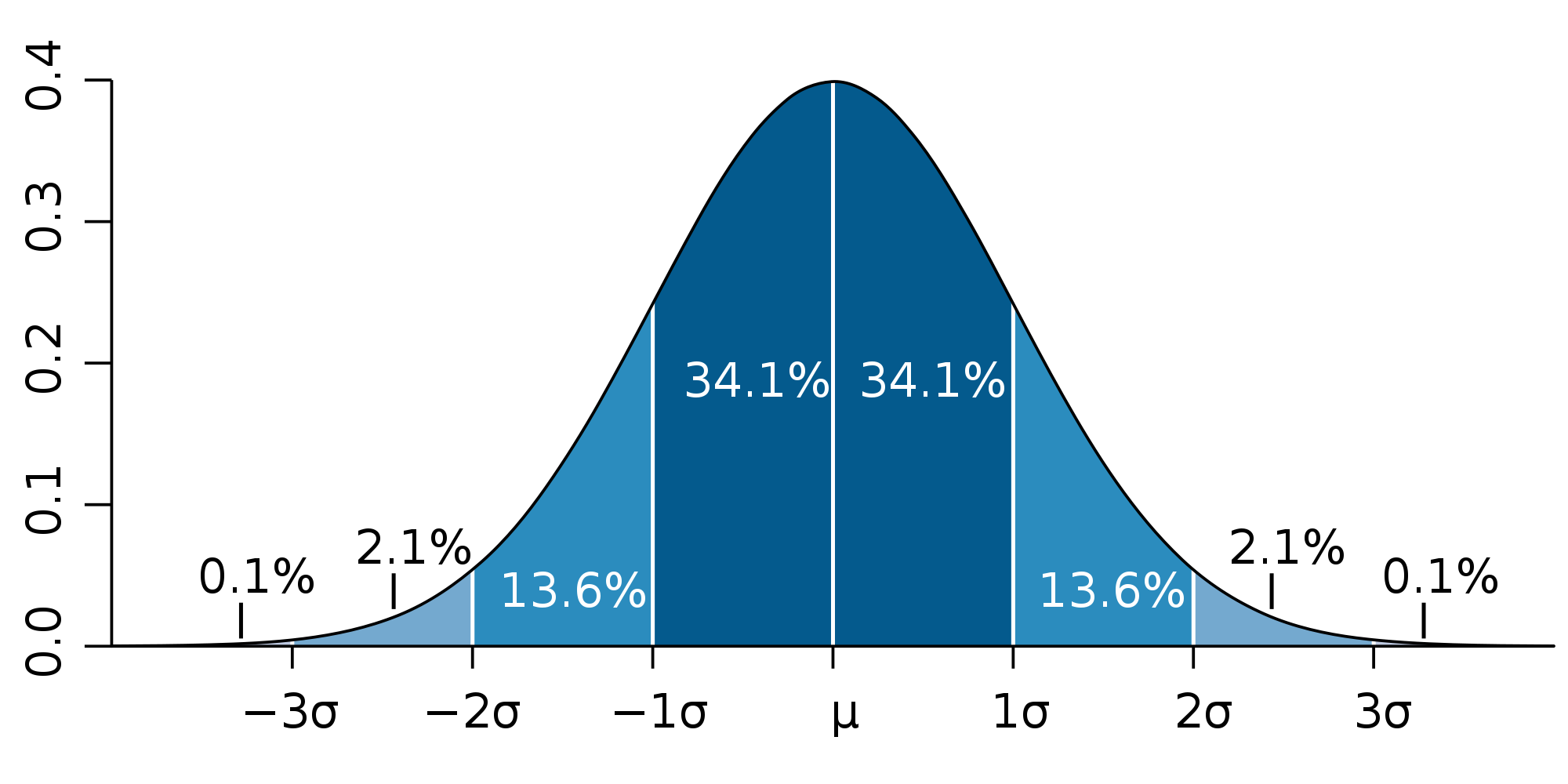
La courbe ci-dessus montre que 0,1 % des morceaux (soient, 14 morceaux) ont une surface supérieure à la valeur moyenne + 3 fois l'écart quadratique moyen.
J'ai retrouvé le quatorzième morceau le plus grand : il avait une surface de 125 cm² (1).
(1) : on acceptera cette valeur comme une donnée du problème.
(2) : on acceptera cette hypothèse comme une donnée du problème.
Quelques calculs maintenant :
La surface moyenne de mes morceaux a une valeur de 280000 / 14000 soit 20 cm².
L'écart quadratique moyen de ces morceaux s'établit à (125 - 20) / 3 = 35 cm².
J'en conclus que 0.1 % des morceaux ont une surface inférieure à 20 - (3 * 35) = - 85 cm² !
Et là, il y a un blème  . Quelqu'un pourrait-il m'expliquer cette incohérence ?
. Quelqu'un pourrait-il m'expliquer cette incohérence ?
PS : Si j'ai pu assez précisément calculer la surface du papier, et peut-être un peu moins précisément l'aire des plus grands morceaux et celle des plus petits, comment ai-je pu à posteriori, avoir une idée, même approximative, du nombre de morceaux arrachés, sachant que je ne sais pas exactement le nombre d'heures que j'y ai passé, pas plus que le nombres de morceaux arrachés à la minute ?
Spoiler : [Afficher le message] On peut considérer cette question comme un indice  .
.
Spoiler : [Afficher le message] Toute l'ambiguïté de ce problème tient à un article...
Spoiler : [Afficher le message] Plus précisément, à l'utilisation d'un article indéfini  .
.
Spoiler : [Afficher le message] Il n'existe pas qu'une seule sorte de loi normale...
Je laisse un temps assez conséquent pour permettre la participation de tous ceux qui vont butiner ailleurs et ne viennent plus sur ce site que de manière épisodique.

 Accueil
Accueil
 Forum
Forum







