 |
#1 - 10-06-2017 17:57:42
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Il y a un blmèe !
Je vous soumets ce petit problème issu d'une mésaventure qui m'est arrivée dernièrement.
Dans un temps fort fort lointain, j'avais fait choix pour tapisser une chambre d'enfant, d'un papier peint vendu comme "lavable, non stripable".
Je n'ai pas regretté mon choix quand il s'est agi d'effacer les gribouillis des petits monstres et j'ai aussi apprécier plus tard sa très bonne tenue dans le temps.
Mais, ce fut une autre affaire quand, les enfants ayant quitté le nid familial, j'ai voulu le décoller pour changer la déco.
La première couche était effectivement parfaitement étanche et a résisté aussi bien au produit de décollage qu'à la vapeur d'eau bouillante.
Il me restait donc qu'à attaquer cette première couche à la spatule, en décollant un petit coin et en tirant précautionneusement de manière à enlever un morceau le plus grand possible.
Il m'a fallu deux jours pour arriver à bout de cette tâche : si parfois, j'arrivais à décoller un morceau supérieur à un dm², la plupart du temps cela se chiffrait en dizaines de cm², et pour le plus petit, à à peine plus de 2 cm² !
J'évalue finalement à environ 14000 (1) le nombre de morceaux arrachés pour venir à bout des 28 m² (1) de papier peint de cette chambre.
Compte tenu de la disparité aléatoire des surfaces et du nombre de morceaux obtenu, on peut raisonnablement penser que ces surfaces sont réparties suivant une courbe de Gauss (2) (Merci Klim  ): ):
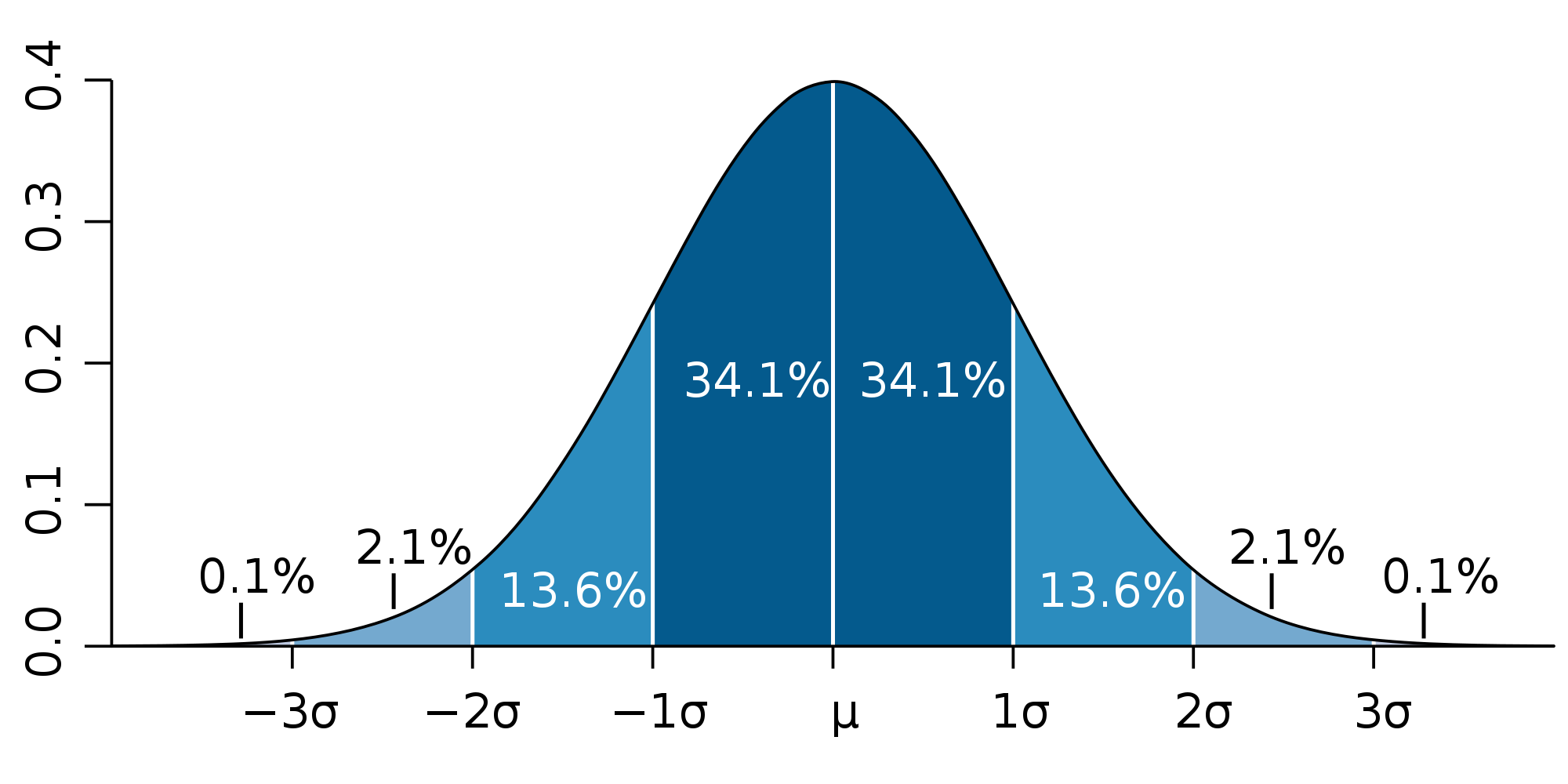
La courbe ci-dessus montre que 0,1 % des morceaux (soient, 14 morceaux) ont une surface supérieure à la valeur moyenne + 3 fois l'écart quadratique moyen.
J'ai retrouvé le quatorzième morceau le plus grand : il avait une surface de 125 cm² (1).
(1) : on acceptera cette valeur comme une donnée du problème.
(2) : on acceptera cette hypothèse comme une donnée du problème.
Quelques calculs maintenant :
La surface moyenne de mes morceaux a une valeur de 280000 / 14000 soit 20 cm².
L'écart quadratique moyen de ces morceaux s'établit à (125 - 20) / 3 = 35 cm².
J'en conclus que 0.1 % des morceaux ont une surface inférieure à 20 - (3 * 35) = - 85 cm² !
Et là, il y a un blème  . Quelqu'un pourrait-il m'expliquer cette incohérence ? . Quelqu'un pourrait-il m'expliquer cette incohérence ?
PS : Si j'ai pu assez précisément calculer la surface du papier, et peut-être un peu moins précisément l'aire des plus grands morceaux et celle des plus petits, comment ai-je pu à posteriori, avoir une idée, même approximative, du nombre de morceaux arrachés, sachant que je ne sais pas exactement le nombre d'heures que j'y ai passé, pas plus que le nombres de morceaux arrachés à la minute ?
Spoiler : [Afficher le message] On peut considérer cette question comme un indice  . .
Spoiler : [Afficher le message] Toute l'ambiguïté de ce problème tient à un article...
Spoiler : [Afficher le message] Plus précisément, à l'utilisation d'un article indéfini  . .
Spoiler : [Afficher le message] Il n'existe pas qu'une seule sorte de loi normale...
Je laisse un temps assez conséquent pour permettre la participation de tous ceux qui vont butiner ailleurs et ne viennent plus sur ce site que de manière épisodique.
#2 - 11-06-2017 10:04:07
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
il y a un nlème !
Peut-être parce que ce n'est pas la bonne analyse à faire pour comprendre la courbe.
En partant de 280000/20=14000, tu considères une proportion à la surface totale.
Plus ton mur est grand, plus tu as de chances d'arracher de gros morceaux.
En raisonnant en proportion à la taille du mur, avec une progression géométrique, on retrouve tes données.
Je pars d'une taille "raisonnable" et je regarde à chaque fois les morceaux 2,5 fois plus petits par exemple :
2000
800
320
128
51,2
20,5
8,2
3,3
1,3
0,5
0,2
On retrouve presque tes données.
On arriverait à 3cm^2 ou moins pour tes petits morceaux, ce qui semble raisonnable...
#3 - 11-06-2017 12:33:07
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Il y a un blème
Pour toute loi normale, il y a une probabilité non nulle d'avoir des valeurs négatives, le blême est ici le choix de la loi qui est inappropriée...
#4 - 11-06-2017 12:55:57
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
#5 - 11-06-2017 17:57:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Il y a uun blème !
Pour moi il y a un vice dès le départ : on prend le modèle général qu'on applique à un cas où certains aléas sont fixés : la répartition statistique va évidemment changer 
Imagine qu'on jette 3 dés et qu'on les range en ordre croissant puis qu'on somme les 3 , on peut facilement calculer l'espérance de cette somme . Maintenant si on sait que le deuxième dé vaut 5 , je crains qu'il n'y ait quelques modification dans cette espérance .
Je ne rentre pas dans les détails car je ne connais rien aux statistiques 
Vasimolo
#6 - 11-06-2017 21:08:03
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
im y a un blème !
On peut effectivement tomber sur les données exactement, mais cela sous entend des morceaux tellement petits qu'on ne les compte pas et une énorme coïncidence statistique pour 20 et 125. On tombe sur des morceaux plus grands que 280000 mais il y en aurait moins de 1, donc pas de souci si on intègre la donnée "nombre de morceaux entier".
Donc, mon "à peu près" me parait raisonnable pour suffire à expliquer le paradoxe.
#7 - 12-06-2017 09:51:40
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Il yy a un blème !
vasimolo : je ne pense pas qu'il s'agisse de ce problème.
gwen : c'est bien, tu as compris le principal.
Je précise que toute cette histoire m'est effectivement arrivée et que les valeurs avancées reflètent assez bien la réalité.
J'ajoute une question subsidiaire : si j'ai pu assez précisément calculer la surface du papier, et peut-être un peu moins précisément l'aire des plus grands morceaux et celle des plus petits, comment ai-je pu à posteriori, avoir une idée, même approximative, du nombre de morceaux arrachés  ? ?
#8 - 12-06-2017 16:03:26
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Il y a un blèe !
Pour préciser un peu, l'erreur à aussi été de prendre les 14 plus gros morceaux pour évaluer l'écart type, car je pense qu'il s'agit d'un estimateur très mauvais, déjà car il ne tient compte que d'un seul morceau, et car la disparité des plus grands morceaux est assez élevée. (le calcul des estimateurs est compliqué car on ne connait pas la fonction de répartition explicite de la loi normale, mais on peut l'approximer par une loi de Gumbel, ce qui nous donne une convergence de la variance de pi^2/( 12*ln(n) ), avec n le nombre de valeurs).
Je pense qu'en utilisant à la fois les valeurs minimales et maximales, on approchera mieux la variance...
Pour l'estimation du nombre de morceaux arrachés, je me demande bien, la logique aurait été de faire la moyenne entre les plus grand morceaux et les plus petits, car la loi normale est symétrique mais ce n'est pas le cas ici, ce qui semble m'indiquer que la loi normale n'est vraiment pas appropriée...
#9 - 12-06-2017 22:42:32
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
il y a un blèmz !
caduk : je suis entièrement d'accord avec toi sur la plupart de tes remarques  . Il te manque juste une petite étape pour arriver au bout de ton raisonnement. . Il te manque juste une petite étape pour arriver au bout de ton raisonnement.
Pour être plus clair, je pourrais ajouter qu'on peut faire l'hypothèse que ces surfaces sont rigoureusement réparties suivant une courbe de Gauss, c'est à dire qu'il n'y a pas de disparité dans la distribution.
#10 - 12-06-2017 22:58:10
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
il y a in blème !
Pour moi, le principal blème, c'est quand tu penses "raisonnable" que les surfaces soient réparties selon une courbe de Gauss.
Si tu arrachais un certain nombre de morceaux dans des endroits de ta chambre tous différents, alors oui, ça ferait sans doute une courbe de Gauss.
Mais avec ton protocole, une fois une bonne partie de papier peint arraché, les derniers arrachages ne pourront engendrer que des petits morceaux. De cette façon, les différents arrachages ne sont pas indépendants, et le théorème central limite ne s'applique pas.
#11 - 13-06-2017 09:17:09
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Il y a un blème
Ebichu : il est effectivement probable que, dans la réalité, il y ait quelque disparité dans la répartition des aires. Mais certainement pas au point d'arriver à l'existence de morceaux inférieurs à -85 cm²  ! !
De plus, dans mon énigme, on fait l'hypothèse que ces surfaces sont rigoureusement réparties suivant une courbe de Gauss.
Se pourrait-il que seul gwen ait trouvé l'explication de ce paradoxe ?
J'ai ajouté un petit indice pour, peut-être, vous mettre sur la voie.
#12 - 13-06-2017 21:10:09
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Il y a un blèm !
Papier difficile => petits morceaux fréquents => discrétisation géométrique probable pour la courbe de Gauss si on veut suivre la loi normale
( j'ai essayé de creuser un peu le sujet )
#13 - 13-06-2017 23:16:18
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Il y a u nblème !
gwen : laquelle  ? ?
caduk (précédemment) : la loi normale est symétrique.
Oui, en coordonnées linéaires tu as raison...
J'ai précisé le deuxième indice.
#14 - 15-06-2017 11:32:59
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Il y a un blèmee !
Sans nouvelle réponse depuis plus d'un jour, je relance le débat avec un Énorme indice  . .
#15 - 17-06-2017 08:12:15
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Il y a unn blème !
Merci  à tous ceux qu ont tenté de percé le mystère de cette énigme. à tous ceux qu ont tenté de percé le mystère de cette énigme.
Félicitation à gwen  qui en a eu tout de suite l'intuition. qui en a eu tout de suite l'intuition.
Eh oui ! Tout est normal dans l'énoncé, seulement il y a la loi normale linéaire et la loi normale logarithmique et mes surfaces se répartissent suivant une loi Log-normale comme la très grande majorité des valeurs mesurables qui appartiennent à l'ensemble des Réels positifs.
Il en est ainsi pour les distances, les surfaces, les masses, les durées, les cours en bourse ou les prix dans un super marché, les relevés de température (exprimés, évidemment, en température absolue), les dénombrements de populations ou d'événements, ou bien, la répartition des ages dans une population, etc...
Ainsi, par exemple, on peut trouver sur le site "Prise de tête" (par ailleurs, un très bon site, pour lequel je recommande une fréquentation assidue !) des statistiques sur l'age des participants. On y apprend que le nombre d'inscrits est à ce jour légèrement supérieur à 100 000, que leur age moyen est de 33,12 ans avec un écart quadratique moyen de 11 ans.
On peut alors en déduire qu'un peu plus d'une centaine de participants ont plus de 66 ans (ce qui est sans doute en dessous de la réalité) et à peu près autant ont moins d'un mois et demi, ce qui laisse présager que certains sont encore à l'état de ftus  !!! !!!
On devrait donc dire que, dans le cas général, les répartitions suivent plutôt une loi log-normale et que l'écart quadratique moyen est à calculer, non pas sur les valeurs mesurées, mais sur les rapports entre ces valeurs.
Si on représente l'ensemble des valeurs mesurées en coordonnées semi-logarithmiques, elles se répartissent alors sur une courbe de Gauss.
La loi normale, elle, n'est qu'un cas particulier à réserver aux valeurs évoluant sur l'ensemble des réels (positifs et négatifs) même si elle peut fournir une approximation correcte pour des mesures strictement positives à condition que l'écart quadratique moyen reste très petit devant la valeur moyenne.
Même dans les cas où la loi normale parait bien s'appliquer sur des valeurs positives, c'est que l'écart quadratique moyen est faible devant la valeur moyenne, et ce serait tout aussi bien (et sans doute encore mieux) avec une loi log-normale  . .
Pour l'estimation du nombre de morceaux arrachés, je me demande bien, la logique aurait été de faire la moyenne entre les plus grand morceaux et les plus petits, car la loi normale est symétrique
Bravo caduk  , c'est bien ainsi que j'ai procédé. Sauf que, puisque la loi est symétrique en coordonnées semi-logarithmiques, il faut faire une moyenne géométrique et non arithmétique. , c'est bien ainsi que j'ai procédé. Sauf que, puisque la loi est symétrique en coordonnées semi-logarithmiques, il faut faire une moyenne géométrique et non arithmétique.
En partant de la taille des grands morceaux évaluée à 125 cm² et de celle des petits évaluée à ~ 3.2 cm², j'obtiens une valeur moyenne de 20 cm², d'où mes 14 000 morceaux.
#16 - 18-06-2017 22:58:30
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Il y a un blèmme !
J'ai bâti cette énigme (à partir d'une expérience réelle), après avoir constaté la méconnaissance parmi les scientifiques de la nécessité d'utiliser la loi Log-normale dans le cas de valeurs évoluant sur R+. Et ce, notamment sur Wikipédia où il y est fait une petite allusion, mais où on la considère plutôt comme un cas particulier de la loi "classique".
J'ai constaté avec un peu d'étonnement la même méconnaissance parmi les "matheux" de P2T (bravo encore à gwen  qui a tout de suite tilté) et je m'attendais donc à quelques réactions sur mes conclusions à l'issue de cette énigme. qui a tout de suite tilté) et je m'attendais donc à quelques réactions sur mes conclusions à l'issue de cette énigme.
J'avoue que je suis un peu déçu du silence étourdissant qui vient frapper mes oreilles  ... ...
#17 - 19-06-2017 00:53:28
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Il y a un bèlme !
Tu dis dans ton énoncé que "ces surfaces sont réparties suivant une courbe de Gauss". Et, dans ta solution, que oui, c'est une courbe de Gauss, mais en coordonnées semi-logarithmiques. C'est un peu triché... Pour moi, c'est pas une courbe de Gauss.
Dirais-tu que la représentation graphique de la fonction exponentielle est une droite ? Parce qu'en coordonnées semi-logarithmiques, c'est vrai. Je ne remets pas en cause l'intérêt culturel de ton exercice, mais sous cette formulation, je trouve qu'il était difficile de voir où tu voulais en venir.
#18 - 19-06-2017 09:45:12
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Il y a un blme !
Je reconnais lambiguïté et je conçois ton trouble. Mais si j'avais dit que la courbe de Gauss était en coordonnées semi-logarithmique, il n'y aurait plus eu d'énigme  ! Peut-être aurais-tu préféré que je dise "ces surfaces sont réparties suivant une loi normale" ? ! Peut-être aurais-tu préféré que je dise "ces surfaces sont réparties suivant une loi normale" ?
Dirais-tu que la représentation graphique de la fonction exponentielle est une droite ? Parce qu'en coordonnées semi-logarithmiques, c'est vrai.
En effet, pourquoi pas ? Je vais essayer de réfléchir (pour plus tard) à une énigme exploitant cette confusion   ! !
#19 - 19-06-2017 12:26:43
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
I ly a un blème !
Peut-être aurais-tu préféré que je dise "ces surfaces sont réparties suivant une loi normale" ?
J'imagine que ça aurait été moins piégeux, mais on ne peut pas refaire le match...
|
 |

 Accueil
Accueil
 Forum
Forum







