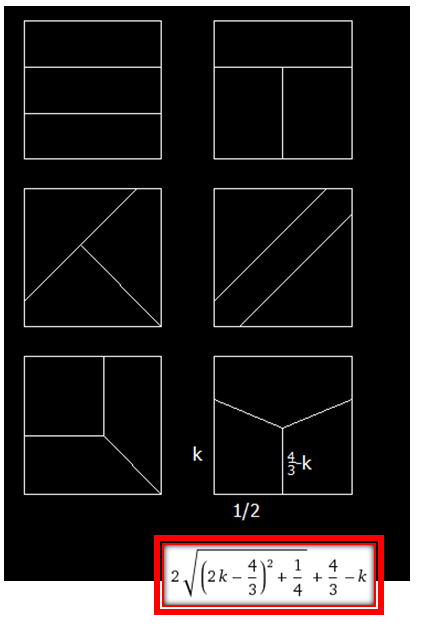
Si je ne me suis trompé nulle part...
J'essaie de découper mon carré de la façon ci-dessous (avec les traits en bleu, ceux en rouge servant de traits de construction) :
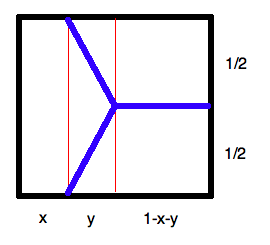
La surface de la zone de gauche vaut [latex]x + \frac{y}{2} = \frac{1}{3}[/latex] d'où [latex]x = \frac{1}{3} - \frac{y}{2}[/latex]. C'est la seule contrainte, car si cette aire vaut 1/3, les deux autres aussi, forcément.
On veut minimiser la longueur de la séparation, qui est deux fois la longueur des traits obliques de gauche plus la longueur du trait "horizontal" de droite :
[TeX]2 \sqrt{y^2+\frac{1}{4}} + (1-x-y)[/TeX]
soit, en remplaçant [latex]x[/latex] par [latex]\frac{1}{3} - \frac{y}{2}[/latex] :
[TeX]2 \sqrt{y^2+\frac{1}{4}} + \frac{2}{3} - \frac{y}{2}[/TeX]
Comme j'ai la flemme de dériver ce truc et de chercher pour quel y entre zéro et un la dérivée s'annule, je demande à Wolfram|Alpha qui me répond
[TeX]y = \frac{1}{2 \sqrt{15}}[/TeX]
et la longueur bleue y vaut [latex]\frac{2}{3}+\frac{\sqrt{15}}{4} \approx 1.635[/latex].
On doit pouvoir trouver légèrement mieux, mais je ne vois pas comment...
Edit : bah tiens, Halloduda et Clems86 ont la même 
Accueil
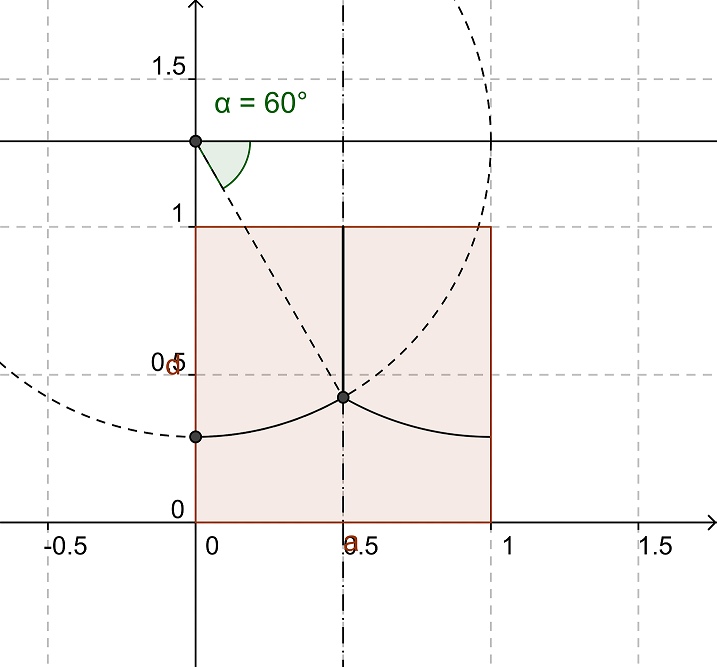1.623278144...
