|
#1 - 12-01-2015 22:56:45
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
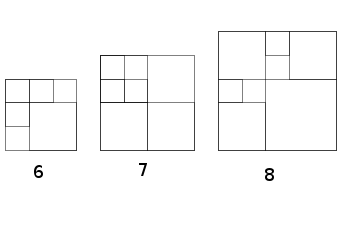
Puzles carrés
Un marchand de jouets fabrique des puzzles carrés avec des pièces carrées, qui peuvent être de tailles différentes, mais dont l'assemblage final est un carré. Le nombre de pièces est inscrit sur chaque boîte. Quels nombres ne pourront jamais y être inscrits ?
Par exemple, le nombre "2" ne pourra pas y être inscrit car on ne peut pas former un carré avec deux carrés plus petits.
La case-réponse valide tous les nombres "impossibles" séparés par un tiret du signe moins.
#2 - 12-01-2015 23:19:36
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
uzzles carrés
2-3-5 
du moins, ça se valide dans la case réponse 
#3 - 13-01-2015 07:20:39
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Puzzles carréés
2-3-5
On peut le faire avec 1.
On peut le faire avec 6 et 8 en entourant un carré sur deux côtés avec des carrés de dimension 1/2 ou 1/3.
Or, si on peut le faire avec n, on peut le faire avec n+3 en coupant un carré en 4.
#4 - 13-01-2015 11:50:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
puzzles cartés
Bonjour Franky
En coupant un carré en quatre on ajoute 3 pièces au puzzle ce qui incite à regarder modulo 3 . On peut trouver facilement un puzzle à 1 , 6 ou 8 pièces ce qui règle le cas de tous les puzzles à plus de 5 pièces .
Il n'y a plus qu'à montrer que 2 , 3 et 5 sont impossibles 
Vasimolo
#5 - 13-01-2015 12:01:26
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
puzzled carrés
On ne pourra pas fabriquer des puzzles de 2, 3 et 5 pièces  . .
#6 - 13-01-2015 22:59:08
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Puzzles crrés
2-3-5 ! 
Quant à prouver que ce n'est pas possible pour 5...
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#7 - 14-01-2015 19:09:16
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
pizzles carrés
Seulement 2, 3 et 5.
Pour 2, c'est impossible, si on ajoute un carré à côté d'un autre, pour que ça colle il faudrait le même côté, donc on a un rectangle de proportion 1x2
Pour 3, même raisonnement, soit le côté est le même pour les deux premiers : le troisième devrait être un rectangle, soit le second est plus petit que le premier, dans ce cas le troisième devrait contenir une forme en L trop complexe pour un simple carré.
Pour 5, pareil, une fois qu'on en a posé 2, on arrive vite à la même conclusion.
Pour 4 ça marche et c'est trivial. Il suffit de le couper en 4.
Par ailleurs, quand ça marche, quel que soit le nombre de carrés, il suffit d'en prendre un et de le couper en 4. Donc si N marche, alors (N-1)+4 = N+3 aussi.
Du coup, si on arrive à en trouver 3 de suite, tous les autres marchent.
6 marche, avec un carré de côté 2 et 5 carrés de côté 1 tout autour.
Puisque 4 marche, 4+3=7 marche
Enfin, avec 4 carrés on peut faire un rectangle de ratio 2x5 (deux carrés identiques côte à cote suivis de deux carrés avec moitié moins pour côté), mais aussi 3x5 (avec un gros carré de côté 3, deux de côté 1 et un de côté 2)
En les mettant côte à côte, on obtient donc un carré de 8 blocks, un peu comme ça
Et ensuite comme on l'a dit, 9 marche puisque c'est 6+3, 10 pour 7+3, 11 pour 8+3, etc...
#8 - 14-01-2015 22:08:45
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Puzzles carérs
Il y a sûrement plus simple.
#9 - 15-01-2015 10:11:15
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Puzzles arrés
salut.
en considérant qu'un jeu avec une pièce n'est pas encore un puzzle , alors il est impossible de découper 2 , 3 & 5 carrés dans un carré sans y laisser un carré ou un rectangle .
#10 - 15-01-2015 22:12:56
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
puzzles varrés
1) On voit qu'on peut réaliser 1 (dur le puzzle !) mais qu'on ne peut réaliser 2, 3, 5 : chaque coin du grand carré doit être occupé par un petit carré, ce qui mène facilement à des impossibilités.
2) Tout nombre pair n>=4 se réalise ainsi :
n=2k avec k >= 2 : on dispose dans un carré de côté k : 1 carré de côté k-1 et 2k-1 carrés de côté 1
3) D'autre part, si n se réalise, alors n+3 aussi, en coupant un carré en 4.
4) D'après 2) et 3), tout nombre impair n>=7 se réalise.
Conclusion : Les nombres impossibles sont 2, 3 et 5.
#11 - 16-01-2015 07:55:54
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Puuzzles carrés
Merci à tous pour votre participation. D'ailleurs tout le monde avait trouvé. On pouvait en effet remarquer que si on savait faire pour N carrés, alors ça marchait aussi pour N+3 carrés. Quant à démontrer rigoureusement qu'avec 5 carrés c'est impossible, je suis un peu dépourvu.
#12 - 16-01-2015 11:45:42
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
puzeles carrés
Voici une démonstration rigoureuse et détaillée :
On suppose qu'il existe un puzzle carré fait de 5 pièces carrées.
1) Chacun des 4 coins du puzzle est occupé par un carré différent.
2) Le 5ème carré est placé contre un bord :
Supposons le contraire. On appelle c1, c2, c3, c4 les côtés des carrés en coin. Alors, on devrait avoir c1+c2 = c2+c3 = c3+c4 = c4+c1, donc c1=c3 et c2=c4. On prend comme unité de mesure le côté du puzzle. Pour que les carrés disposés dans des coins opposés ne se chevauchent pas, il faut c1<=1/2 et c2<=1/2. Ce qui force, avec c1+c2=1, à avoir c1=c2=1/2=c3=c4. Il ne reste alors plus de place pour le 5ème carré. C'est absurde.
3) On appelle c5 le côté du carré placé au bord, disons entre les carrés de côté c1 et c4. On obtient alors :
c1+c2=c2+c3=c3+c4=c4+c5+c1, ce qui donne c1=c3 et c2=c4 donc c5=0
C'est absurde. CQFD.
#13 - 16-01-2015 16:35:35
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Puuzzles carrés
Bravo titoufred. Ta réputation de ténor de P2T n'est pas usurpée.
#14 - 17-01-2015 18:04:30
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Puzzles arrés
Les puzzles 3D sont à la mode 
Et si on remplace les carrés par des cubes ?
Vasimolo
#15 - 06-02-2015 16:59:53
- PtiteMeuf
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 1
puzzkes carrés
La réponse est 2-3-5 (a mon avis ce n'est pas la seule bonne réponse mais en tout cas c'est validé).
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum