 |
#1 - 21-07-2017 16:30:59
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Un polyomino qui s'auo entoure.
Hello les gens!
Imaginez voir une forme polygonale qui peut s'entourer avec des copies d'elle même sans laisser de segment à l'air libre. C'est facile un simple carre ça marche, vous l'accolez à 4 copies de lui même dans les 4 directions.
Mais le nombre clef est ici 4. Le jeu c'est de faire moins. Non seulement c'est faisable mais en plus on peut atteindre 2 ce qui est clairement le minimum.
Cette tuile par exemple le fait:
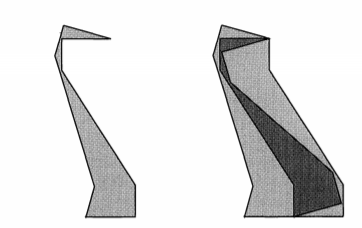
(Elle est bien d’épaisseur non nulle partout "Voderberg Tile")
Et donc mon défi:
Trouver un polyomino qui minimise le nombre de copies de lui même nécessaire pour s'entourer ainsi.
Je rappelle qu'un polyomino est un assemblage de carrés par exemple:
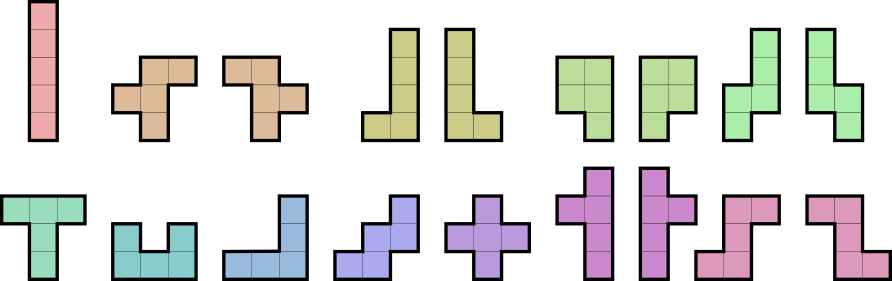
Moi ce qui m’intéresse c'est surtout d'atteindre 2, après quelques heures de réflexions et de recherche (et j'espere qu'il n'existe pas de solution triviale dans des pistes autres que celles que j'ai) je me dit que c'est pas forcement impossible. Il y a de l'espoir et a priori si la solution existe elle est satisfaisamment tordue.
Bonne chance!
#2 - 22-07-2017 18:25:50
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Un polyomino qui s'uto entoure.
@sydre: Je ne suis pas sur de saisir d´ou vient ta formule et le raisonnement ne semble pas spécifique aux polyominos. (Et si c'est un raisonnement general sur le périmètre il est nécessairement faux puisque des polyedres avec la propriété existent)
#3 - 23-07-2017 10:28:31
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Un polyomino qqui s'auto entoure.
@sydre: il me faudrait un petit schema pour voir comment tu utilises cette propriété dans notre cas.
#4 - 24-07-2017 02:42:08
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
un pilyomino qui s'auto entoure.
Après réflexion j'ai répondu un peu vite, je reviendrai 
#5 - 24-07-2017 19:10:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Un polyomino qui s'auto entorue.
Je ne sais pas quelle idée tu as en tête Clydevil , mais tu n'as aucune chance de construire ton polyomino sur le même principe que l'ennéagone de Voderberg .
Aussi petit soient-ils les carrés surpportent mal les rotations de 15° 
Mais bon , une jolie bête qui me fait vaguement penser à un clip de Stromaë .
Vasimolo
#6 - 24-07-2017 20:54:09
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
un pilyomino qui s'auto entoure.
Il n'y a pas forcément besoin d'un rotation de 15 degrés pour construire un objet répondant au contraintes de Clydevil. La tuile de Voderberg est un exemple qui le vérifie (et possède de plus des propriétés de pavage) mais on peut facilement en construire une multitude d'autres sur le même principe, avec un angle différent (voire avec des bords courbes...)
En revanche, il est impossible d'utiliser un angle de 90 degrés, ce qui ne permet pas d'adapter directement dans le cas de polyomino. J'ai tenté des constructions différentes, notamment avec l'une des images en position miroir, mais ça n'a rien donné pour l'instant...
Les seuls résultats que j'ai pour l'instant sur les polyominos sont que l'une au moins des répliques doit être tournée de 90 degrés, et le polyomino doit comporter au moins 3 angles rentrants. (Très facile de démontrer qu'il en faut au moins 2)
#7 - 24-07-2017 22:36:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Un polyomiino qui s'auto entoure.
Tu peux donner un exemple d'un polygone qui n'est pas une simple déformation de celui de Voderberg (avec un minimum de côtés ) ? Sinon je crois aussi que c'est impossible pour les polyominos pour une raison de parité .
Vasimolo
#8 - 24-07-2017 22:51:13
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
un polyomino qui s'auto entourr.
Avec un minimum de côté, il sera très semblable à la tuile de Voderberg, qui laisse assez peu de marge de manoeuvre, mais on peut trouver un autre angle légèrement différent de 15 degrés.
On augmentant le nombre de côtés, on peut pas mal augmenter cet angle. (Je pense qu'il serait intéressant de chercher l'angle maximal...)
#9 - 25-07-2017 09:33:28
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Un polyomino qui s'auto entoure
@Vasimolo: Si on ne peut pas faire avec 15degres il faut chercher avec 90. Je suis arrivé aux mêmes conclusions que ci dessus. Mais pour le moment je n'ai pas d'argument qui démontrent une impossibilité.
#10 - 25-07-2017 10:52:18
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
Un polyomino qui s'ato entoure.
Le hic est que, pour que la forme « englobante » constituée des deux duplicatas de la figure ait un « volume » il faut que la somme des traits non utiles (ne couvrant pas un côté de la figure de base) soit supérieure à la somme des traits utiles, autrement dit, le périmètre de deux figures serait supérieur au double de celui d'une seule.
#11 - 25-07-2017 11:19:25
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Un polyomino qui s'auto entouure.
@gwen27: Je ne suis pas sur de suivre ton raisonnement. Je ne vois pas d'argument général que tu puisses utiliser sur le périmètre (voir la tuile de Voderberg en exemple dans le post initial qui réalise l'objectif).
D'autre part soit P le périmètre d'une forme alors le périmètre au sens large de deux formes c'est 2P qui se trouve partagé:
-En segments utiles (à l’intérieur couvrant la première forme) de longueur total P.
-En segments ni utiles ni à l'exterieur de l'ensemble (peut être que les 2 formes qui entourent se touche sur une longueur non nulle.)
-En segments à l’extérieur.
Et du coup lorsque c'est possible le périmètre extérieur de l'ensemble des 3 copies c'est au maximum P (2P-P-0) et parfois moins. Dans le cas Vorderberg c'est P.
#12 - 25-07-2017 11:40:27
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
Un polymino qui s'auto entoure.
Oui, mais là, c'est impossible, car on est sur une maille carrée.
On peut avoir une forme aussi tarabiscottée que l'on veut, le nombre de traits vers le haut ou vers le bas dans la figure centrale s'équilibre. Il reste une "hauteur simplifiée" que l'on doit doubler. (idem pour la largeur)
Si tu veux entourer cette forme, il te faudra plus que cette hauteur et plus que cette largeur, ce que l'on n'a pas car à la jonction des deux formes "englobantes" on doit rajouter au moins une épaisseur.
Ceci dit, cela tient au fait que les deux formes englobantes sont identiques à la forme initiale, donc, quelles que soient leurs orientations, la somme des traits verticaux et horizontaux sera constante.
#13 - 25-07-2017 11:55:49
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
un polyomino qui s'zuto entoure.
@Gwen27: Non rien ne force à ajouter une épaisseur, ça dépend de la manière dont les deux formes englobent la première mais elles peuvent très bien se toucher par un coin et ainsi n'avoir que des segments utiles ou des segments vers l’extérieur.
J’attire l'attention sur cette variation de la tuile de Voderberg:
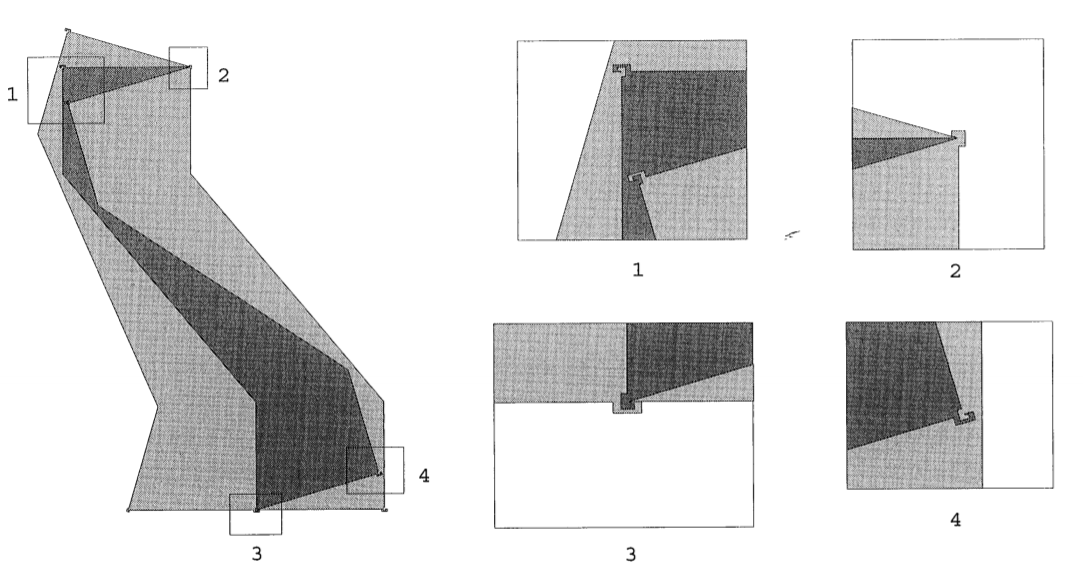
(zoom possible)
Dans cette variation des modifications ont été faites pour garantir une épaisseur non nulle partout dans la coque d'encerclement. Ce qui prouve qu'avoir des segments ni a l’extérieur ni a l’intérieur n'invalide pas la possibilité d'atteindre notre objectif.
Je vais réfléchir si on peut tirer un truc de ton argument de division horizontale/vertical des segments. Il y en a sans doute hein, la je signale juste 2 points qui me semblent "pas si simple" 
#14 - 25-07-2017 12:05:53
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
un polyomino qui s'auto entouee.
Pars de formes englobantes et d'une forme englobée quelconque...
Tu peux triturer, agrandir, déformer, déplacer, bref, chercher les formes que tu veux ... Le périmètre des formes rouges sera toujours supérieur de 4 (au moins, car j'ai entouré au plus court) au double de la forme intérieure sur une maille carrée.

#15 - 25-07-2017 12:29:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Un polyomino qui s'auto entore.
Oui , c'est super bien vu !!!
Il fallait y penser 
Vasimolo
#16 - 25-07-2017 13:46:31
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
un polyomino qui s'auto entpure.
Allow me to disagree 
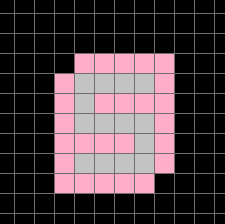
#17 - 25-07-2017 14:06:01
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
Un polyomino quii s'auto entoure.
Ce n'est pas faux, mais cette "épaisseur" t'oblige tout de même à avoir des pièces plus larges et/ou plus longues que la forme initiale.
La somme des largeurs et des longueurs des pièces ne collera pas. Si la pièce de base s'inscrit dans un rectangle n x m, les deux autres doivent s'inscrire dans un rectangle (n+2) x (m+2).
#18 - 25-07-2017 14:46:55
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Un polyomino qui s''auto entoure.
J'avais avancé le même argument que @gwen27 : reste à le démontrer proprement ...
#19 - 25-07-2017 15:24:45
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Un polyoomino qui s'auto entoure.
I disagree (mais ça me fait réfléchir donc on s'approche petit a petit soit d'une vrai démo d’impossibilité soit de contraintes à respecter  ) )
Ici on a bien la contrainte sur le périmètre et la contrainte sur le rectangle englobant respectée (tout rentre dans du 6x7)

#20 - 25-07-2017 19:09:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Un polyomino qui s'auto enttoure.
Je suis de plus en plus persuadé que ça ne collera pas pour des raisons de parité 
Faire un polygone à neuf côtés en suivant les lignes d'un quadrillage carré c'est très risqué . Après on peut ciseler tant qu'on veut , on ne changera pas la parité .
Vasimolo
#21 - 25-07-2017 23:52:05
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Un polyomino qui s'auto ntoure.
@Vasimolo: Mais c'est quoi cette obsession de 9 cotes et de vouloir faire un analogue de la tuile de Voderberg avec des polyominos? en quoi le nombre impair de cote est une feature nécessaire? en quoi la tuile de voderberg serait la seule qui répond au prob?
#22 - 26-07-2017 12:19:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Un polyomino quui s'auto entoure.
#23 - 26-07-2017 12:59:04
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
un poltomino qui s'auto entoure.
@Vasimolo: Oui on est limite en rotation, j'ai fait pareil je suis partie de Voderberg et j'ai tente avec la rotation de 90, on aboutit à une contradiction dans les cas que j'ai teste.
Globalement on peut voir le problème comme un mapping. On a le périmètre P de notre figure initial qui est P=R1(S1).R2(S2) la concaténation de deux morceaux (ou R1 est une rotation qcq dans 0 -90 +90 -180) et S1 et S2 soit des morceaux de P. Ca laisse quand même pas mal de possibilités meme sans la symétrie axiale. Meme pour R1=180 je ne vois pas d'argument propre pour declarer quil faut nécessairement mapper R1(S1) sur S1.
Il semble à peut pres certain (mais c'est pas non plus tres rigoureux) de voir que R1=0 ou R2=0 ne donnera pas grand chose et donc on se retrouve avec de base 9 cas possibles plus d'eventuelles translations pas encore très claire dans ma tete pour chacun de ses cas. Ca fait quand meme pas mal de cas....
Pour deconer ca cest ce que je triturais lorsque je faisais le meme mapping que voderberg

Cest le meme mapping c'est a dire R180(S1) sur S1 et R90(S2) sur le debut de S1. Pas d'ambalement ca marche pas du tout, mais c'est pas pour une des raisons précédemment évoquée. Ps: je cherche avec des polygones parceque je pars du principe qu'a la contrainte de l'angle de rotation prés (angle de 90 degres que je respecte) on peut pixeliser un polygone comme il faut pour en faire un polyomino qui fonctionne. Mais peut etre que cette assumption est fausse.
#24 - 26-07-2017 13:46:22
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Un polyomnio qui s'auto entoure.
Salut !
Bon, pour 3 je propose :

Voilà 
#25 - 26-07-2017 14:02:04
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Un polyomino qiu s'auto entoure.
@golgot59: Tres bien! et ya une etape intermediare que tu peux chercher si ca t'amuse c'est 3 copies en assurant une epaisseur non nulle partout.
|
 |

 Accueil
Accueil
 Forum
Forum














