Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 08-08-2013 17:17:26
Les cônes t la sphèreBonjour,
#0 Pub#2 - 09-08-2013 08:29:06
Les cônnes et la sphèreOn trouve r=38.490017945975... soit environ 38.490018 cm #3 - 09-08-2013 09:12:20#4 - 09-08-2013 18:07:11#5 - 09-08-2013 18:19:01#6 - 09-08-2013 20:58:04
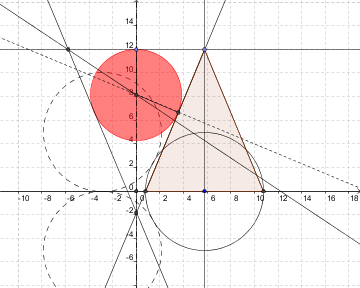
Les cônes et la pshèreJe m’intéresse d’abord à l’axe de symétrie "révolutionnaire" de ce système qui passe par le centre de la sphère et le barycentre du triangle équilatéral formé par les trois centres des cercles de base des cônes. #7 - 10-08-2013 14:24:28
Les cônes et la sphèrBonjour, Il y a sûrement plus simple. #8 - 10-08-2013 17:23:44#9 - 11-08-2013 19:04:14
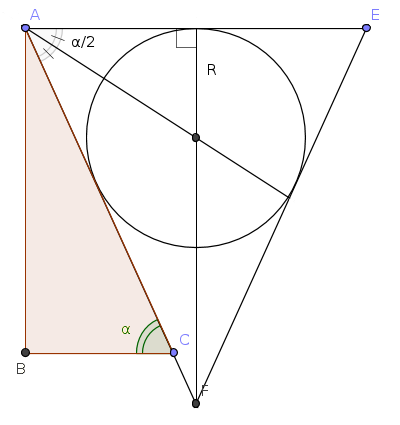
Les cônes et la sphèrreOn peut remarquer que si r1 désigne le rayon de la sphère inscrite dans l'un des cônes alors le rayon cherché vaut r3=r1sin(π3) . Plus généralement si on répartit régulièrement n cônes sur un cercle alors le rayon de la sphère coincée entre ces cônes vaut rn=r1sin(πn) . #10 - 12-08-2013 10:34:58
Les cônes et la sphèrC'est astucieux: avec n cônes régulièrement répartis sur un #11 - 12-08-2013 11:49:59
Les cônse et la sphèreMerci à vous pour les généralisations. #12 - 12-08-2013 12:11:26
les cônes ey la sphèreAjoutons par ailleurs qu'il y a un nombre maximal de cone à mettre sur un cercle pour respecter les conditions du problème. Il faudra avoir 2*rn<H soit #13 - 12-08-2013 16:03:44
les vônes et la sphère@kossi_tg: #14 - 12-08-2013 16:41:46#15 - 12-08-2013 18:14:45
les cônrs et la sphèreUn dessin à l'échelle acrédite la formule de Vasimolo: j'ai dû me gourrer quelquepart. Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.