La même que la distance moyenne entre l'extrémité d'un demi-cercle et tous les points de ce demi-cercle. (L'intégrale sur une surface est double, mais la 2ème intégrale de 0 à pi autour du diamètre du demi-cercle ne change rien à l'affaire)

Soit 2/pi * l'intégrale de 0 à pi/2 de 2*cos a  (LATEX, c'est pas mon truc ).

(L'intégrale de 0 à pi/2 à partir d'une extrémité du diamètre est beaucoup plus simple que celle de 0 à pi en partant du centre.)

C'est à dire 4/pi, soit pas loin de 1.27324 .

Modification : ajout de la figure et du texte en italique.

Salut,
Je pense que telle que posée la question n'a pas de réponse:
http://fr.wikipedia.org/wiki/Paradoxe_de_Bertrand
C'est un paradoxe qu'il est très important de bien comprendre lorsqu'on demande des probabilités pour certains objets d'appartenir à tels sous ensemble, lorsque les espaces considérés ont plus d'une dimension. (Je pense qu'ici également dans un calcul de moyenne le même genre de problèmes s'applique).
En résumé on ne peut pas poser ce genre de question en faisant abstraction de la méthode décrivant la densité de nos objets sur leur espace.
Bien sur ici je pense que tous le monde comprendra qu'une extrémité est choisie au hasard equipondérée sur la sphère et que l'autre l'est ensuite de manière indépendante, mais comme il est toujours très difficile d'assurer qu'il n'y a qu'un interprétation...

C'était juste une intervention de partage culture math j'ai la flemme de faire ce genre de calculs (quelque soit la méthode)

Bonjour,
La distance moyenne est aussi celle entre le "pôle nord" et les points du "globe terrestre". Dans un repère "comme il faut", le "pôle nord" est le point (0;0;1).
D=V[x²+y²+(1-z)²] et comme x²+y²+z²=1 on aura D=V(2-2z) ou D=(2-2z)^0,5
On intègre sur toute la sphère en faisant varier z de -1 à +1, soit:
D=(1/2)x(-1/3)[(2-2z)^1,5]entre-1et+1=(-1/6)x(0-4^1,5)=8/6=4/3
Je trouve finalement D=4/3
Bonne soirée.
Frank

Nous pouvons considérer la moyenne des distances D depuis un point A quelconque de la sphère.
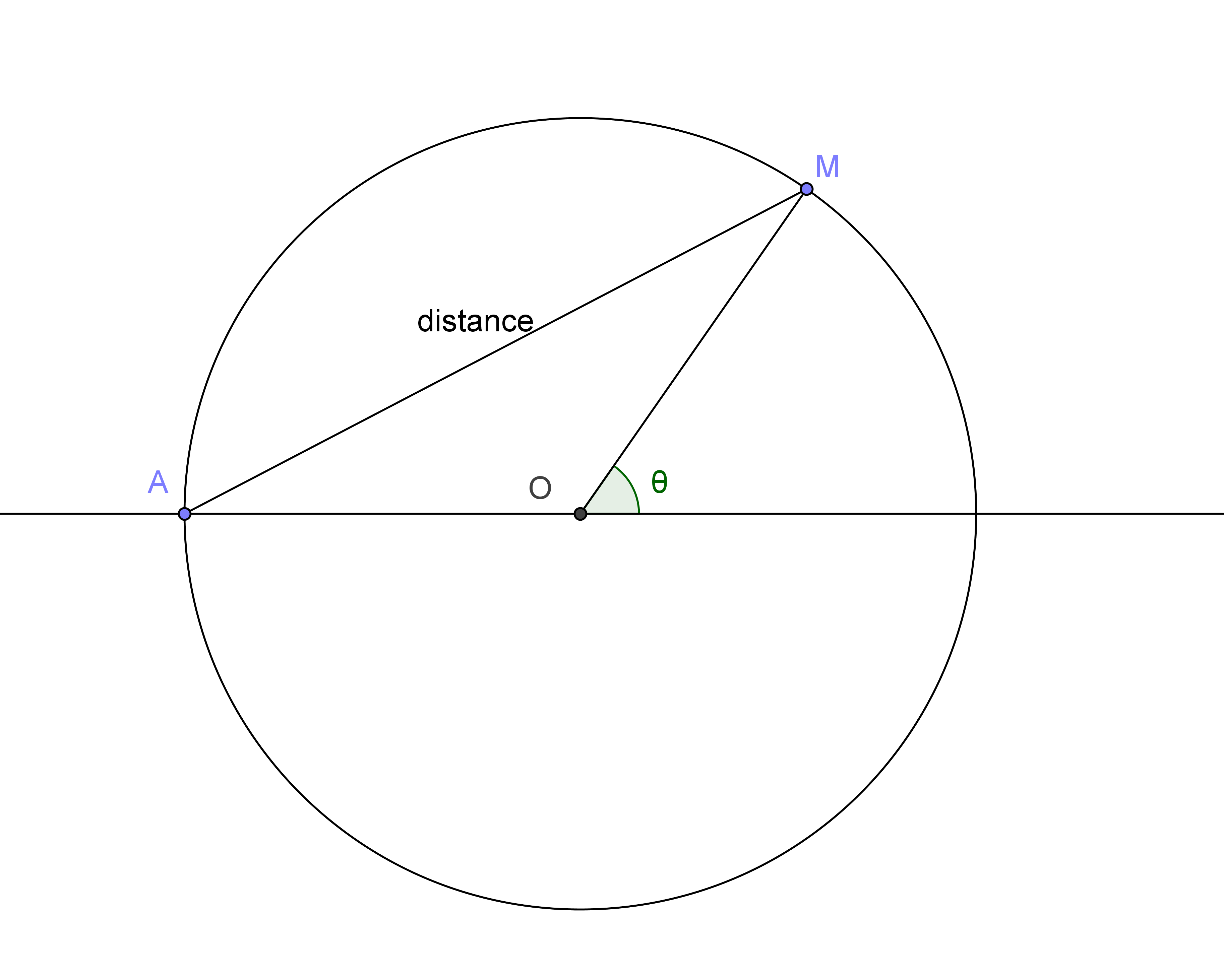[latex]D=\frac{\int_{\theta=0}^{\pi}{2\pi\sin{\theta}*{2\cos\frac{\theta} 2}d\theta}}{\int_{\theta=0}^{\pi}{2\pi\sin{\theta}d\theta}}[/latex]
[TeX]D=\int_{\theta=0}^\pi {\sin\theta*\cos{\frac{\theta} 2}} d\theta}[/TeX]
soit, en posant [latex]\phi=\frac{\theta} 2[/latex]
[TeX]D=\int_{\phi=0}^{\frac{\pi} 2}{2\sin{\phi}\cos^2{\phi}d\phi}[/TeX]
et en posant [latex]\cos\phi=x[/latex]
[TeX]D=-2\int_{x=1}^{-1}{x^2dx}[/TeX]
soit [latex]D=\frac 4 3[/latex]

Je m'étonne que ce petit problème qui m'est tout de suite apparu comme évident n'est pas été résolu par la pléiade de matheux fréquentant ce site et que seul DSK pardon FMI soit de mon avis. J'avais comme lui tester mon résultat sur Excel avec une très bonne cohérence et seulement 45 points entre 1 et 89°.
J'attends le verdict d'Ef'  ...

J'ai ajouté une figure et quelques explications sur le 1er message.

Personnellement, je peut interpreter le probleme de 3 facons differentes:
Prenons le 1er point A au pole nord de la sphere, et B le 2eme point.
1) pour chaque point B, trouver la moyenne des lignes droites en suivant la courbure de la sphere, pour tous les angles possibles. Donner la fonction de cette moyenne en fonction de la distance la plus courte entre A et B.
2) donner la moyenne des distances entre A et B (our tous points B sur la sphere), en ligne droite au travers de la sphere.
3) donner la moyenne des distances entre A et B (our tous points B sur la sphere), en ligne droite en suivant la courbure de la sphere.

Je suppose que le vrai probleme est le 2eme, mais dans tous les cas je n'ai pas de réponse.

fmi a écrit:

raisonnons sur un demi cercle

l'angle  A qui sous tend la corde varie aleatoirement entre 0 et pi.

la corde vaut 2*sin(A/2)

La valeur moyenne est l'integrale de 2*sin(A/2) entre zero et pi; le tout divisé par pi

Le calcul elementaire de cete integrale donne 4/pi soit environ 1.273


Le calcul avec la fontion alea sur un tableur avec 10000 essais donne effectivemnt un moyenne  variant en gros 1.265 et 1.285

C'est aussi ce que j'avais fait. Je note qu'il y a un groupe répondant 4/3. Que dit l'arbitre?

Je détaille ma réponse ! La bonne réponse est évidemment 4/3.
Dans [latex]\mathbb{R}^3[/latex] on considère la sphère unité [latex]x^2+y^2+z^2=1[/latex].
On considère le point fixe [latex]A=(1,0,0)[/latex] et le point variable
[TeX]M=(x,y,z)=\left(x,y,\sqrt{1-x^2-y^2}\right)[/TeX]
sur l'hémisphère nord, paramétré par [latex](x,y)[/latex]. Alors
[TeX]AM=\sqrt{(1-x)^2+y^2+z^2}=\sqrt{2-2x}[/TeX]
La distance moyenne [latex]\ell[/latex] cherchée est égale à l'intégrale double sur le disque unité [latex]D^2[/latex] (on divise par la surface [latex]2\pi[/latex] de l'hémishère nord)
[TeX]\ell =\frac{1}{2\pi} \iint_{D^2}\sqrt{2-2x}\,\left\Vert \frac{\partial M}{\partial x}\wedge\frac{\partial M}{\partial y}\right\Vert dx\,dy[/TeX]
[TeX]
\ell =\frac{1}{2\pi} \iint_{D^2}\frac{\sqrt{2-2x}}{\sqrt{1-x^2-y^2}} dx\,dy[/TeX][TeX]\ell = \frac{1}{2\pi}\int_0^1\int_0^{2\pi}\frac{r\,\sqrt{2-2r\cos t }}{\sqrt{1-r^2}}\,dr\,dt[/TeX][TeX]\ell=\frac{4}{3}[/TeX]
Voilà ! Pour le petit problème qui est tout de suite apparu comme évident...

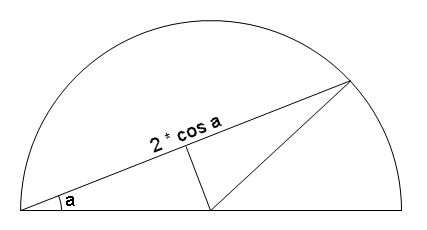
Je ne sais plus pourquoi mais quand j'ai fais un dessin d'un demi-cercle de rayon 1 pour moi c'était trivial que la moyenne était majorée par [latex]2*cos(\frac{\pi}{4})=\sqrt{2}[/latex] soit la diagonale d'un carré de côté 1.

Bonjour,

Quelle est la distance moyenne en ligne droite entre 2 points pris sur une sphère de rayon 1 ?

j'interprète l’énoncé autrement, il s'agit de distance sur une surface à 2 dimensions à courbure positive, ici, une sphère.


Soit a et b, 2 points quelconques sur une surface sphérique. Il n'existe qu'une ligne droite passant par deux points sur une sphère, sa géodésique, ici un cercle de rayon sphère (r).
Avec a et b confondu (par exemple), la distance mini est 0 et comme la géodésique est fermée, on obtient  la distance maxi: [latex]2\pi.r[/latex]. La moyenne est [latex]\frac {0+2.\pi.r} 2 = \pi.r[/latex]. Avec [latex]r=1[/latex] on trouve [latex]\pi[/latex] comme distance moyenne.
La distance moyenne en ligne droite entre deux points serait alors sur Terre d'approximativement 20 100 km.
En gros, il existe sur une sphère deux chemins (sens) possibles pour joindre en ligne droite deux points, la distance moyenne est toujours la même quelque soit la position des deux points, elle n'est fonction que du rayon.

Trop simple?

Bonjour,
A la surface d'une sphère, la distance moyenne serait évidemment pi R / 2. Mais la question posée ici est la distance moyenne "à travers la sphère" et il y aurait deux "écoles": 4R / 3 ou 4R / pi: ça se complique un peu.
Bonne journée.
Frank

Salut,

Franky1103 a écrit:

Bonjour,
A la surface d'une sphère, la distance moyenne serait évidemment pi R / 2. Mais la question posée ici est la distance moyenne "à travers la sphère" et il y aurait deux "écoles": 4R / 3 ou 4R / pi: ça se complique un peu.
Bonne journée.
Frank

justement, il n'est nullement précisé "à travers la sphère", mais "sur la sphère", ça fait une sacrée différence. il faudrait peut-être réécrire l'énoncé.

J'allais oublier, bonnes fêtes à tous vos neurones.