 |
#1 - 14-06-2022 18:05:47
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Dernier terme d'une suite infinei
Pour changer, je ne vous demanderai pas quel est le terme suivant, mais plutôt quel est le DERNIER terme de cette suite logique, une fois arrivé au bout 
100, 200, 300, 301, 302, 303, 304, 309, 350, 351, 352, 353, 354, 359, 355, 356, 357, 358, 360, 361, 362, 363, 364, ...
Ce qui est amusant : cette suite peut être infinie (suivant les avis) - mais pourtant elle admet un dernier terme 
#2 - 14-06-2022 18:19:24
- clanelle
- Passionné de Prise2Tete
- Enigmes résolues : 0
- Messages : 77
Dernire terme d'une suite infinie
Bonjour,
Dans la suite que tu donnes ("100, 200, 300, 301, 302, 303, 304, 309, 350, 351, 352, 353, 354, 359, 355, 356, 357, 358, 360, 361, 362, 363, 364, ..."), 359 est avant 355 alors qu'elle semblait jusque là strictement croissante.
Est-ce une erreur de transcription ou confirmes-tu ?
Lionel
#3 - 14-06-2022 19:02:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
detnier terme d'une suite infinie
C'est vrai que si elle est constante à partir d'un moment , elle a une infinité de termes mais un nombre fini de valeurs .
Vasimolo
#4 - 14-06-2022 20:54:00
- lecanardmasqué
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 607
DDernier terme d'une suite infinie
Bonsoir.
Nombre dans l'ordre alphabétique si l'on prend leur écriture en chiffres romain
100 C
200 CC
300 CCC
301 CCCI
302 CCCII
.
.
.
.
etc
Et donc le dernier terme est 38 ( XXXVIII )
Sympa cette suite 
#5 - 14-06-2022 21:31:40
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Dernier terme d'une siute infinie
@Vasimolo : je parle un nombre fini de termes dans le cadre d'une suite finie, ou un nombre infini de termes distincts dans l'autre hypothèse. Et pourtant, quelle que soit l'hypothèse retenue, il y a bien un dernier terme.
@clanelle : j'ai fait exprès d'en mettre autant justement pour montrer cette particularité, qui n'est donc pas une erreur (ni une exception, même si on peut facilement expliquer pourquoi c'est pas aussi fréquent)
Edit : et. bonne réponse du canard masqué 
#6 - 15-06-2022 07:29:50
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Dernier terme d'une suite inffinie
Liste des chiffres romains classés par ordre alphabétique: le dernier est XXXVIII = 38
#7 - 15-06-2022 09:50:31
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
dernier terme f'une suite infinie
Bonne réponse de Franky1103
#8 - 15-06-2022 09:59:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Dernier terme d'uune suite infinie
C'est malheureusement trop facile avec les outils d'aujourd'hui 
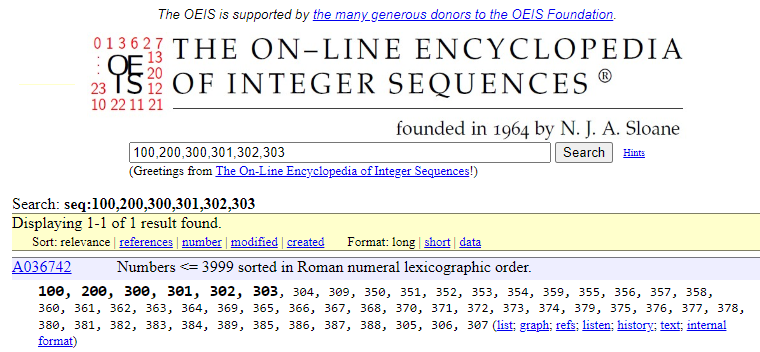
Donc XXXVIII , le dernier en ordre alphabétique .
Vasimolo
#9 - 15-06-2022 10:18:28
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Dernier terme d'une suite innfinie
Ah oui en effet :-( Je l'ai codé, pour ma part, c'était bien fun :-)
#10 - 15-06-2022 10:26:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
DDernier terme d'une suite infinie
Une remarque un peu "technique" à propos de la question : "Quel est le dernier terme de la suite ?"
La question n'a pas vraiment de sens "mathématique" . Si on n'accepte qu'un nombre fini de termes : ce n'est pas une suite . Si on en admet une infinité alors disons que le premier est U0 et le dernier Un , n termes , ce n'est pas cohérent . Cette liste n'est pas une suite , d'ailleurs il y a des trous dans la liste impossible à compléter en respectant l'ordre alphabétique sans donner une borne aux entiers listés .
Vasimolo
#11 - 15-06-2022 10:46:30
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Dernier erme d'une suite infinie
Pas tout à fait d'accord, mais ça promet d'être un débat passionnant...
Je mets en spoil, parce que ça pourrait donner des idées même si la réponse n'apparaitra pas par magie 
Spoiler : [Afficher le message]
* Tu me demandes Un pour n'importe quelle valeur de n, je peux te la calculer
* Tu me demandes quel est l'indice n d'une valeur k=Un... là j'ai un peu plus de mal...
* Sauf pour le dernier bien entendu, je peux te donner le terme suivant
* Je me demande si c'est "en pratique" une bijection qui ne serait pas démontrable "en théorie"
EDIT : je retire les phrases
* A une exception près, je peux te donner le terme précédent
* à 54 exceptions près (pas grand chose au regard de l'infini), je peux aussi te donner tous les termes précédents jusqu'au premier
elles sont fausses, il y a une infinité de cas
#12 - 15-06-2022 11:09:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Derniier terme d'une suite infinie
Je pense qu'il faut mettre le débat en pause tant que le masque n'est pas levé 
Juste une réponse rapide pour "Tu me demandes Un pour n'importe quelle valeur de n, je peux te la calculer"
Je suis sûr que non et tu vas sans doute le reconnaitre . Le dernier terme de ta suite est un Un parmi une infinité d'autres , U0 aussi . Tu veux donc ranger une infinité d'entiers naturels ( tous distincts ) dans un intervalle limité par le plus petit et le plus grand des Ui ( i variant de 0 à n ) .
Vasimolo
#13 - 15-06-2022 11:36:57
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Dernier terme d'une suiet infinie
Je prends le défi, envoie moi un "n" et je te donne le "Un" correspondant - par MP
#14 - 17-06-2022 02:29:57
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
eDrnier terme d'une suite infinie
Salut,
Ces premiers termes sont ceux de la suite des nombres romains triés par ordre lexicographique. Et effectivement la réponse attendue est 38 (XXXVIII).
Je suis d'avis que cette suite est finie: la numération romaine n'étant pas définie au delà de 3999 
Si s'autorise à compter au delà (avec une infinité de symboles totalement ordonnés) alors bien sur c'est une permutation de N.
#15 - 17-06-2022 16:55:16
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Dernier terme d'unee suite infinie
Beaucoup de bonnes réponses, à savoir 38. Il s’agit bien des nombres écrits sous forme romaine, triés par ordre alphabétique : rien n’existe après XXXVIII (alphabétiquement parlant)
C’est une énigme logique et pas mathématique mais elle a donné lieu à quelques discussions passionnantes avec notre chef pâtissier :-)
En gros, une « relation d’ordre » en mathématiques est un moyen de trier des éléments d’un ensemble, comme les nombres entiers par exemple. > ou < sont des relations d’ordre par exemple. Et le tri alphabétique des écritures romaines aussi.
On appelle aussi le plus petit élément d’un ensemble (son PPE) l’élément qui est plus petit que tous les autres, par rapport à cet ordre. Logique. Et vous comprendrez facilement aussi ce qu’est le plus grand élément (PGE).
Pour > et <, avec lesquels on a l’habitude de travailler, si un ensemble d’entiers admet un PPE et un PGE, alors il est fini.
L’ensemble des nombres positifs impairs admet un PPE (c’est 1) mais pas de PGE, il est donc infini.
L’ensemble des nombres compris entre 42 et 4242 admet un PPE (42), un PGE (4242) et il est donc fini.
Ce qui est remarquable, c’est que cette règle qui paraît super intuitive ne l’est pas du tout : elle est même fausse ! Ou plus exactement elle nécessite une propriété supplémentaire, à savoir que l’ordre et l’ordre réciproque sont de « bons » ordres.
Sans rentrer dans les détails, on voit bien ici que l’ensemble de tous les entiers est
- infini, j’espère que personne n’en doute
- admet un PPE (100 - C)
- admet un PGE (38 - XXXVIII)
Un autre exemple simple : une relation d’ordre définie par : « tout est plus petit que 1, et pour le reste on regarde la relation < »
Dit de manière impropre, c’est comme « prendre 1 et le mettre à la fin de tous les entiers »
Quoi qu’il en soit, l’ensemble des entiers naturels admet 0 pour PPE et 1 pour PGE mais n’en est pas moins infini
Sur ce, bon week end 
#16 - 17-06-2022 19:27:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
dernier terme s'une suite infinie
Pour compléter ce que dit Scarta et sans rentrer dans des détails . On considère l'écriture romaine de base ( sans les ajouts historiques ) , on peut empiler les M à volonté .
Il n’y a aucun problème pour ranger tous les nombres entiers par l’ordre alphabétique de cette écriture , il y aura un premier élément C et un dernier XXXVIII . La question semble résolue mais il y a un problème .
Pour le comprendre il faut imaginer un dictionnaire contenant tous les mots possibles avec un nombre fini de lettres . Le nombre de mot est dénombrable dans le sens ou on peut les ranger dans un ordre 1 , 2 , 3 , 4 … qui va permettre de récupérer n’importe quel mot en comptant suffisamment longtemps . Maintenant si on liste les éléments de ce dictionnaire en respectant l’ordre alphabétique alors : A , AA , AAA , … , on n’atteindra jamais le mot AB qui n’est pourtant certainement pas à la fin du dictionnaire .
Il y a la même faille dans la suite de Scarta , le mot nombre 38 (XXXVIII ) comme beaucoup d’autre ne sera jamais atteint par la suite . En fait la suite tend vers l’infini , ce qui est assez évident car tous les termes sont des entiers naturels distincts .
Je pinaille bien sûr mais la rédaction du problème encourageait à le faire .
Vasimolo
#17 - 18-06-2022 23:41:31
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Dernier tere d'une suite infinie
Et pour conclure j’ajoute le point suivant : dans l’exemple du dictionnaire, les seuls mots qu’on y lira sont de la forme AAAAA…AAAA.
Dans le cadre des nombres romains c’est tous ceux dont la valeur modulo 1000 n’est pas entre 5 et 8, ni entre 10 et 49, ni entre 90 et 99.
Je laisse les lecteurs démontrer pourquoi 
|
 |

 Accueil
Accueil
 Forum
Forum







