 |
#1 - 08-10-2008 20:21:31
- zikmu
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 277
J'ai encore un epu les boules...
Je dispose de 12 boules parfaitement identiques d' aspect, bref il est impossible de les différencier à l'oeil et au toucher.
Par contre, elles font toutes le même poids, sauf une...qui a donc un poids différent...
Je dispose également d'une balance de Roberval...
Comment faire, en 3 pesées maximum pour identifier cette boule, et dire si elle est plus ou moins lourde que les autres ?
#2 - 08-10-2008 22:21:43
- Passetemps
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 405
J'ai encore unn peu les boules...
Sur 12 boules dont une est plus lourde.
Je pose 4 boules sur le premier plateau et 4 autres sur le deuxième.
Deux cas se présentent
1er cas :
A-La balance penche d'un côté
1-J'enlève les boules du plateau plus léger et je prend les quatres boules plus lourdes de l'autre plateau.
2-Je pose ces quatres boules, à raison de deux sur chaque plateau.
3-J'enlève les boules du plateau plus léger et je prend les deux boules plus lourdes de l'autre plateau.
4-Je pose ces deux boules, à raison d'une sur chaque plateau.
5-Le plateau plus loud gagne
2ème cas :
B-La balance est en équilibre
1-J'enlève toutes les boules des plateaux et je prend les quatres boules restantes.
et je répète les opérations 2,3,4 et 5
Sur 12 boules dont une est plus lègère, je fais les mêmes opérations mais en conservant les boules du plateau plus léger.
Dans le cas ou l'on ignore si une boule est plus lourde ou plus légère que les autres, hum…., je réfléchis au problème.
#3 - 08-10-2008 23:37:22
- papiauche
- Sa Sainteté
- Enigmes résolues : 49
- Messages : 2131
J'ai encore un peu les boues...
On divise les groupes en trois groupes de 4.
Première pesée:
En cas d'égalité, la boule cherchée est dans le troisième groupe et les huit premières sont neutres.
Dans ce cas, on effectue une deuxième pesée en en prenant trois (notées 9,10,11) dans le quatrième groupe + une neutre.
Si égalité, c'est la dernière (12), une troisième pesée permettant de savoir si elle est lourde ou légère.
Sinon on pèse 9+10 contre deux neutres.
Si 9+10> 11+N, alors:
Troisième pesée:
si 9+11> N+N c'est 9 et elle est lourde
si 9+11 =N+N c'est 10 et elle est lourde
si 9+11> N+N c'est 11 elle est légère.
même raisonnement si 9+10< 11+N:
Troisième pesée:
si 9+11> N+N c'est 11 et elle est légère
si 9+11 =N+N c'est 10 et elle est légère
si 9+11> N+N c'est 11 elle est lourde.
On a conclu en cas d'égalité de la première mesure.
Dans le cas contraire, la boule cherchée est dans les 8 sur la balance et les 4 autres peuvent servir d'étalon.
Cas où 1+2+3+4> 5+6+7+8
Deuxième pesée: 1,2,5 contre 3,6,N
Si 1+2+5>3+6+N alors 1 ou 2 plus lourde ou 6 plus légère
Si 1+2+5=3+6+N alors 7 ou 8 plus légère ou 4 plus lourde
Si 1+2+5<3+6+N alors 5 plus lourde ou trois plus légère.
Cas où 1+2+3+4< 5+6+7+8
Deuxième pesée: 1,2,5 contre 3,6,N
Si 1+2+5>3+6+N alors 5 plus lourde ou 3 plus légère
Si 1+2+5=3+6+N alors 7 ou 8 plus lourde ou 4 plus légère
Si 1+2+5<3+6+N alors 1 ou 2 plus légère ou 6 plus lourde.
Pour la troisième pesée:
cas n°1
n léger ou p Lourd
On effectue une pesée n,p contre deux neutres
Si n+p > N+N alors p Lourd
Si n+p < N+N alors n léger
cas n°2
(n ou p) léger ou q Lourd
On effectue une pesée n,q contre N,N
si n+q<N+N alors n léger
si n+q= N+N alors p léger
si n+q>N+N alors q lourd.
cas n°3
(n ou p) lourd ou q léger
On effectue une pesée n,q contre N,N
si n+q<N+N alors q léger
si n+q= N+N alors p lourd
si n+q>N+N alors n lourd.
Ouf!
Edit: j'ai modifié l'erreur de copier-coller (le coller deux fois donnait deux réponses contradictoires!)
Le cadre d'édition est petit pour ce genre de réponse 
"Je ne lis jamais un livre dont je dois faire la critique. On se laisse tellement influencer." O. Wilde
#4 - 09-10-2008 03:34:20
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
j'ao encore un peu les boules...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#5 - 09-10-2008 20:47:53
- LeSingeMalicieux
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1298
- Lieu: Haute-Marne
j'ai encore un peu les boulzs...
1) sur les 12 boules :
j'en pèse 6 : d'un côté 3 et de l'autre 3
-> la balance est à l'équilibre : la boule X est dans les six boules restantes
--> la balance penche : la boule X est dans les 6 boules pesées
2 ) j'ai 6 boules dont la boule X
j'en prends 3
je les mets d'un côté de la balance, et de l'autre trois boules normales
-> la balance est à l'équilibre : cas A :la boule X est dans les trois dernières, non peées sur ce coup ci
-> la balance penche : cas B : suivant si le plateau où se trouve la boule X penche vers le haut ou vers le bas, on détermine que la boule X est plus légère ou plus lourde
3) il nous reste 3 boules. Suivant le cas (A ou B), nous agirons différemment :
- cas A : il nous reste 3 boules, mais nous ne savons pas si la boule X est plus lourde ou plus légère... On en compare deux sur la balance, si la balance reste à l'équilibre alors la boule X est celle mise de côté ! Sinon, c'est une des deux que nous venons de comparer, mais laquelle...?
- cas B : il nous reste 3 boules, et nous savons si la boule X est plus lourde ou plus légère. On en compare deux sur la balance. Si la balance penche, on sait quelle est la boule X, si elle est à l'équilibre, la boule mise de côté est celle que l'on cherche, et on sait déjà si elle est plus lourde ou plus légère !
Voilà, dans 2/3 des cas je sais, mais il me reste 1/3 des cas où j'ai besoin d'une quatrième pesée...
Avoir quatre mains, c'est plus pratique pour taper sur un clavier.
#6 - 10-10-2008 18:10:05
- fizwizbiz
- Amateur de Prise2Tete
- Enigmes résolues : 41
- Messages : 1
J'ai encore un peu les boules..
on sépart les 12 boules en deux groupes de 6 et on les pèses pour trouvé le tas le moin lourd ou se trouveras evidement la boule la moin lourde.
il faut ensuite séparer le groupe des 6 boules les moin lourde en deux groupe de 3 et on recommence pour retrouvé le groupe le moin lourd. Une fois se groupe trouvé on fait une dernière pesé avec une boule de chaque coté : si les deux boules on le même poid alors la plus lgère est celle qui n'a pa été pesé et si les deux boules sont de poids différent alors il n'est pa difficile de trouvé la plus légère...
#7 - 10-10-2008 19:49:53
- zikmu
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 277
j'ai ebcore un peu les boules...
Bonsoir,
vous avez compris que la difficulté n'est pas tant de trouver la boule différente,
mais de dire si elle est plus lourde ou plus légère.
Je vous propose donc une solution afin de vérifier que c'est bien possible.
Il y en a sans doute d'autres...
Appelons les boules par groupe de 4 : abcd ABCD et 1234
N une boule Normale et O la boule cherchée de poids différent.
( \ : penche à gauche ; / : penche à droite ; =^= : équilibre )
1ere pesée : abcd^ABCD :
si =^= alors O fait partie de 1234 ( et abcdABCD=N )
donc 2nde pesée : abc^123 ( ou NNN^123 ):
si =^= alors O = 4
==> 3ème pesée 4^N pour déterminer si + ou - lourde
si abc/123 alors O = 1,2ou 3 et O est +lourde
==> 3ème pesée 1^2 :
si =^= alors O = 3+, si 1/2 alors O = 2+, si 1\2 alors O = 1+
si abc\123 alors O = 1,2ou 3 et O est +légère
==> 3ème pesée 1^2 :
si =^= alors O = 3-, si 1/2 alors O = 1-, si 1\2 alors O = 2-
si abcd/ABCD alors O est une de ces 8 boules et + lourde si à droite ou + légère si à gauche
donc si O est une minuscule, elle sera forcément + légère et + lourde si elle est majuscule.
reste à trouver O... ( on a également 1234=N bien sûr )
2nde pesée : On retire a et A,on inverse b et B, on remplace C par N (ou 1), on garde d et D ( et c )
si équilibre Bcd^bND alors O = A,a ou C
==> 3ème pesée : A^C : si =^= alors O = a-
sinon si A\C alors O = A+ ou si A/C alors O = C+
si Bcd\bND alors la pesée s'est inversée et O = b ou B
==> 3ème pesée : b^N :
si =^= alors O = B+
sinon O = b- (b\N n'est plus envisageable)
si Bcd/bND alors rien n'a changé et O = d,D ou c
==> 3ème pesée : c^d :
si =^= alors O = D+
sinon si d/c alors O = d- ou si d\c alors O = c-
si abcd\ABCD ==> retourner la balance ou se placer de l'autre côté et voir le cas précédent...Merci
Bonne réponse de Papiauche ( même s'il s'est un peu emmêlé les crayons en copiant-collant je pense au niveau de la 2nde pesée )...merci pour votre réflexion
#8 - 14-06-2011 00:03:17
j'au encore un peu les boules...
Une Solution plus claire s'impose...
12 boules
3 pesées (balance à plateaux)
1 boule de poids différent
determiner la boule diff et si + lourde, + légère.
(=) : équilibre
(/) : penche à gauche
(\) : penche à droite
(1+): boule 1 supposée + lourde
(1-): boule 1 supposée - lourde
(1*): boule 1 supposée normale
PeséeI : [1 2 3 4] - [5 6 7 8]
(=) => PeséeII : [(9)(10)] - [(11)(1*)]
(=) => Pesée III : [(12)] - [(1*)]
(=) => impossible.
(/) => (12+).
(\) => (12-).
(/) => Pesée III : [(9+)] - [(10+)]
(=) => (11-).
(/) => (9+).
(\) => (10+).
(\) => Pesée III : [(9-)] - [(10-)]
(=) => (11+).
(/) => (10-).
(\) => (9-).
(/) => PeséeII : [(1+)(2+)(5-)] - [(3+)(4+)(6-)]
(=) => Pesée III : [(7-)] - [(8-)]
(=) => impossible.
(/) => (8-).
(\) => (7-).
(/) => Pesée III : [(1+)] - [(2+)]
(=) => (6-).
(/) => ((1+).
(\) => (2+).
(\) => Pesée III : [(3+)] - [(4+)]
(=) => (5-).
(/) => (3+).
(\) => (4+).
(\) => PeséeII : [(1-)(2-)(5+)] - [(3-)(4-)(6+)]
(=) => Pesée III : [(7+)] - [(8+)]
(=) => impossible
(/) => (7+).
(\) => (8+).
(/) => Pesée III : [(3-)] - [(4-)]
(=) => (5+).
(/) => (4-).
(\) => (3-).
(\) => Pesée III : [(1-)] - [(2-)]
(=) => (6+).
(/) => (2-).
(\) => (1-).
27 cas :
12 * 2 = 24 + 3 cas impossibles.
#9 - 15-06-2011 19:08:59
- zikmu
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 277
J'ai encore un peu ls boules...
#10 - 15-06-2011 20:01:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
J'ai encore un peu le sboules...
Je me dis qu'une image vaut mieux qu'un discours, Depuis le temps que je la connais sur papier, ça me démangeaist de la mettre en images...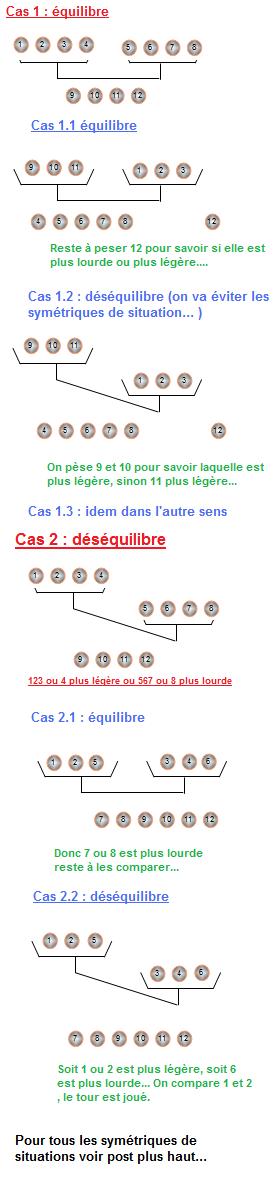
#11 - 15-06-2011 20:14:52
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
j'ai encore un peu leq boules...
La solution en images de Gwen27 est claire et complète.
Bravo et merci.
#12 - 17-06-2011 16:54:30
- zikmu
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 277
J'ai encoe un peu les boules...
Ceci a au moins comme mérite de prouver ce que je disais, il y a plusieurs solutions, donc merci pour ces précisions...
#13 - 06-08-2011 00:11:22
J'ai encorre un peu les boules...
zikmu a écrit:Je dispose de 12 boules parfaitement identiques d' aspect, bref il est impossible de les différencier à l'oeil et au toucher.
Par contre, elles font toutes le même poids, sauf une...qui a donc un poids différent...
Je dispose également d'une balance de Roberval...
Comment faire, en 3 pesées maximum pour identifier cette boule, et dire si elle est plus ou moins lourde que les autres ?
Voir tableau ci-dessous
Pierres A,B,C,D,E,F,G,H,I,J,K,L
Il faut envisager tout les cas de figures ,il faut donc donner
24 réponses soit c'est qui est A lourd ou léger
ou B,C,D,E,F,G,H,I,J,K,L
1er cas
Pesée 1 : A+B+C+D = E+F+G+H
donc A-B-C-D-E-F-G-H = 0 et I-J-K-L = lourd,0, léger
Pesée 2 : A+B+C > I+J+K
donc A-B-C = 0 et I-J-K = 0 ou léger et L = 0
Pesée 3 : I > J donc I = 0 et J = léger et K = 0 Résultat J = léger
Pesée 3 : I = J donc I et J = 0 et K = léger Résultat K = léger
Pesée 3 : I < J donc I = léger, J = 0 et K = 0 Résultat I = léger
2 ème cas
Pesée 1 : A+B+C+D = E+F+G+H
donc A-B-C-D-E-F-G-H = 0 et I-J-K-L = lourd,0, léger
Pesée 2 : A+B+C = I+J+K
donc A-B-C-I-J-K = 0 et L = lourd ou léger
Pesée 3 : A < L donc L = lourd Résultat L = lourd
pesée 3 ; A > L donc L = léger Résultat L = léger
3 ème cas
Pesée 1 : A+B+C+D = E+F+G+H
donc A-B-C-D-E-F-G-H = 0 et I-J-K-L = lourd,0, léger
Pesée 2 : A+B+C < I+J+K
donc I-J-K = 0 ou lourd et L = 0
Pesée 3 : I < J donc J lourd et J-k = 0 Résultat J lourd
Pesée 3 : I = J donc K lourd et I-J = 0 Résultat K lourd
Pesée 3 : I > J donc I lourd et J-K = 0 Résultat I lourd
4ème cas
Pesée 1 : A+B+C+D < E+F+G+H
donc A-B-C-D = léger ou 0 et E-F-G-H- = lourd ou 0 et I-J-K-L = 0
Pesée 2 : A+B+E < C+D+F
Donc A-B = léger ou 0 et C-D-E = 0 et F = 0 ou lourd
Pesée 3 : A < B donc B = léger Résultat B léger
Pesée 3 : A = B donc F = lourd Résultat F lourd
Pesée 3 : A > B donc A = léger Résultat A léger
5ème cas
Pesée 1 : A+B+C+D < E+F+G+H
donc A-B-C-D = léger ou 0 et E-F-G-H- = lourd ou 0 et I-J-K-L = 0
Pesée 2 : A+B+E = C+D+F
donc G-H = 0 ou lourd
pesée 3 : G < H donc H = lourd Résultat H lourd
Pesée 3 : G > H donc G = lourd Résultat G lourd
6ème Cas
Pesée 1 : A+B+C+D < E+F+G+H
donc A-B-C-D = léger ou 0 et E-F-G-H = lourd ou 0 et I-J-K-L = 0
Pesée 2 : A+B+E > C+D+F
donc A-B = 0 et C-D = 0 ou léger et E = 0 ou lourd
Pesée 3 : C < D donc E = 0 et C = léger Résultat C léger
Pesée 3 : C = D donc C et D = 0 et E = lourd Résultat E lourd
Pesée 3 : C > D donc E = 0 et D = léger Résultat D léger
7ème cas
Pesée 1 : A+B+C+D > E+F+G+H
donc A,B,C,D = 0 ou lourd et E,F,G,H= 0 ou léger et I,J,K,L = 0
Pesée 2 : A+B+E < C+D+F
Donc A-B-F = 0 et C-D = 0 ou lourd et E = 0 ou léger
Pesée 3 : C < D donc E,C = 0 et D = lourd Résultat D lourd
pesée 3 : C = D donc C,D = 0 et E = léger Résultat E léger
Pesée 3 : C > D donc D,E = 0 et C = lourd Résultat C lourd
8ème cas
Pesée 1 : A+B+C+D > E+F+G+H
donc A,B,C,D = 0 ou lourd et E,F,G,H= 0 ou léger et I,J,K,L = 0
pesée 2 : A+B+E = C+D+F
donc Donc A,B,C,D,E,F = 0 et G,H = 0 ou léger
Pesée 3 : G < H donc G = léger Résultat G léger
Pesée 3 : G > h donc H = léger Résultat H léger
9ème Cas
Pesée 1 : A+B+C+D > E+F+G+H
donc A,B,C,D = 0 ou lourd et E,F,G,H= 0 ou léger et I,J,K,L = 0
Pesée 2 : A+B+E > C+D+F
Donc A,B = 0 ou lourd et F = 0 ou léger et E,C,D = 0
Pesée 3 : A < B donc A,F = 0 B = lourd Résultat B lourd
Pesée 3 : A = B donc A,B = 0 et F = léger Résultat F léger
Pesée 3 : A > B donc B,F =0 et A lourd Résultat A lourd
Avec un tableau on voit mieux mais......
#14 - 08-01-2012 07:07:46
j'ai encore yn peu les boules...
Question pour gwen 27
Si j'ai bien compris l'énoncé , on ne sais pas si la boule différente est PLUS lourde ou MOINS lourde
Du coup pourquoi dans le cas 1.1,poses-l'hypothèse que la boule différente est forcément MOINS lourde et fait donc partie de 9 10 11 ?
Et si elle était PLUS lourde et faisait partie de 1 2 3
#15 - 08-01-2012 19:30:26
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
J'ai encore un peu ls boules...
@Maraclea : s'il y a un déséquilibre entre 9-10-11 et 1-2-3, comme on sait que les boules 1, 2 et 3 sont "normales", le sens du déséquilibre nous dit si la boule anormale est plus lourde ou plus légère.
Si 9-10-11 est plus lourd que 1-2-3, c'est que la boule anormale est plus lourde. Si 9-10-11 est plus léger que 1-2-3, c'est que la boule anormale est plus légère.
Gwen n'a traité qu'un de ces deux cas, et a ajouté une note disant qu'il souhaitait ne pas considérer les "symétriques de situations" 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#16 - 10-01-2012 23:59:44
- karim21
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 3
J'ai ecnore un peu les boules...
bin je crois que la solution est simple  , il faut tt simplement partager les boules en 3 groupes de 4 qui fait donc 12 boules , (G1 G2 et G3) on met le g1 dans un plateau et g2 dans l'autre : on a donc deux cas : Cas1 et Cas2 , il faut tt simplement partager les boules en 3 groupes de 4 qui fait donc 12 boules , (G1 G2 et G3) on met le g1 dans un plateau et g2 dans l'autre : on a donc deux cas : Cas1 et Cas2
Cas1 : les deux plateaux sont équilibrés , donc la boule est dans le g3 , on prends deux boules du g3 on les met dans plateau et les deux autres dans l'autre plateau (ça fais deux pesée) , forcement un plateau va penché , et enfin on prends les deux boules du plateau penché , on met chacune dans un plateau (ca fais 3 pesée) , et sans surprise le plateau ou ya la boule la plus lourde va pencher.
pour Cas2 c'est le même raisonnement que le Cas1
#17 - 11-01-2012 01:04:41
- karim21
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 3
j'ai encpre un peu les boules...
deuxième solution
6 d'un coté et 6 de l'autre (1 pesé)
on prends les 6 boules du plateau penché , et en met trois dans chaque partie de la balance (2 pesé) et forcément un plateau va penché, parmi les 3 boules penché, on prends deux , et en met une dans chaque plateau (3 pesé) si une des boules penche , ça sera celle ci , sinon c'est la troisième .
et il ya meme une troisième solution , au lieu de partager les 6 boules penché dans la deuxième solution en groupe de 3 ,en les partages en groupe de 2 , deux boules dans chaque plateau , bref , je continu pas , vous savez le suite
a+
#18 - 11-01-2012 20:30:50
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
J'ai encore un peu les buoles...
Sauf qu'on ne sait pas si la boule différente est plus légère ou plus lourde que les autres, et ça rend tes solutions caduques...
Bienvenue par ici, en tout cas 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#19 - 14-01-2012 13:31:10
J'ai encore un peeu les boules...
Question pour gwen 27
Si j'ai bien compris l'énoncé , on ne sais pas si la boule différente est PLUS lourde ou MOINS lourde
Du coup pourquoi dans le cas 1.1,poses-l'hypothèse que la boule différente est forcément MOINS lourde et fait donc partie de 9 10 11 ?
Et si elle était PLUS lourde et faisait partie de 1 2 3
#20 - 14-01-2012 16:27:25
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
j'au encore un peu les boules...
Les billes 1-2-3 sont normales dans le cas 1 (ni plus lourdes, ni plus légères). On le sait grâce à la première pesée. Gwen les compare donc avec 9-10-11 :
- si le plateau 9-10-11 est au même niveau que le plateau 1-2-3, c'est donc la boule 12 qui est anormale, plus qu'à vérifier si elle est plus lourde ou légère.
- si le 9-10-11 est au-dessus du 1-2-3, c'est qu'une des trois boules 9-10-11 est plus légère que les deux autres. Plus qu'à trouver laquelle.
- si le 9-10-11 est en-dessous du 1-2-3 (cas non traité car "symétrique"), c'est qu'une des trois boules 9-10-11 est plus lourde.
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#21 - 14-01-2012 17:19:17
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
J'ai encore un eu les boules...
Même plus le temps de répondre aux questions qu'on me pose  
Mais oui, le cas 1 correspond au cas où 1234 s'équilibrent avec 5678, donc, pour ces huits boules là l'incertitude est levée. Elles sont normales.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







