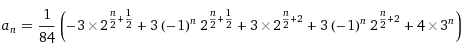Quelle est la 15ème valeur de cette suite ?
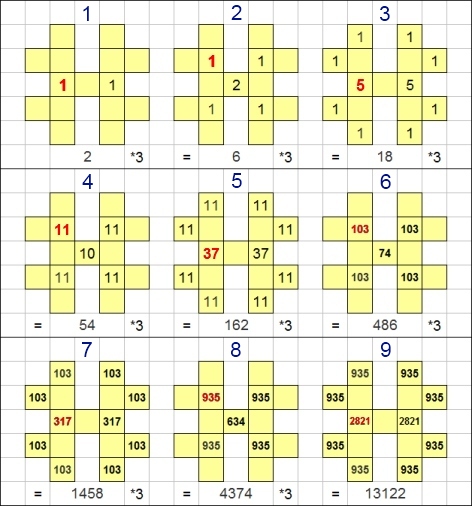
0, 1, 1, 5, 11, 37, 103, 317, 935, 2821, 8431, 25325, 75911, 227797, ...
(le premier terme étant la valeur 0).
Tous les jours j'ajouterai un indice et un terme supplémentaire à cette suite.
N'hésitez pas à me faire part de vos réflexions ou de vos questions, même si vous n'avez pas réussi à valider la case réponse.
Spoiler : [Afficher le message] Merci à toni77 et à gwen27 pour leur aide involontaire dans la définition de cette énigme.
Spoiler : [Afficher le message] Les différents termes peuvent être trouvés grâce à cette formule :
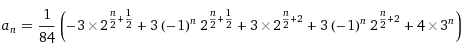
Merci à Memento pour me l'avoir indiquée.
Spoiler : [Afficher le message] ... mais pour ma part je préfère utiliser 2 formules toutes simples, l'une pour les termes pairs, l'autre pour les termes impairs.
Spoiler : [Afficher le message] La case 1 a un certain rapport avec les termes impairs, la case 2 avec les termes pairs (ou bien le contraire, cela dépend d'où on commence la numérotation !).
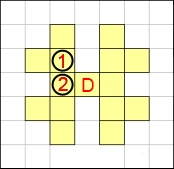
Spoiler : [Afficher le message] La figure précédente illustre l'énigme http://www.prise2tete.fr/forum/viewtopic.php?id=8203 de tony77.

 Accueil
Accueil
 Forum
Forum