Bonjour, je vous soumets l'un de mes tours de magie (vous connaîtrez même le truc !), et mes impressions sur celui-ci :
Prenez 32 cartes. Présentez-les en éventail à quelqu'un, et demandez-lui de choisir secrètement une carte, dans sa tête (admettons qu'il ait pris le 9 de pique). Posez la première de vos cartes sur la table (oui, vous devez être près d'une table !), la deuxième carte à côté, et la troisième carte encore à côté. Posez la quatrième carte sur la première, la cinquième sur la deuxième, la sixième sur la troisième, et de nouveau, la septième sur le premier tas (ce tas étant composé des première et quatrième cartes), etc.
Au final, vous devez normalement poser la 32ème carte sur le deuxième tas.
Vous obtenez donc 3 tas, les deux premiers ont 11 cartes, et le troisième 10. Demandez à votre ami dans quel tas est la carte qu'il a choisie. Prenez ce tas, et placez-le entre les deux autres tas (si le tas où se trouve le 9 de pique est par exemple le tas C, on place le tas C sur le tas B, et on recouvre le tout du tas A. L'inverse est tout à fait possible, du moment que le tas où se trouve la carte est en sandwich).
Et on recommence ce procédé. Personnellement, je fais ceci 4 fois.
A la fin de la quatrième fois, je demande une fois de plus dans quel tas se trouve la carte (admettons que ce soit le tas A). Je prends le tas B, je le place sur la table, avec les cartes bien ordonnées. Ensuite, je prends le tas A, et je place les cartes une par une sur le tas B, d'une manière précise : Je prends la première carte du tas A, et je la place sur le tas B, en la faisant dépasser nettement. Je prends la deuxième carte du tas A, et je la place sur le tout, sans dépasser. L'explication est difficile à formuler, aussi je vous inviterai à regarder plutôt mon dessin : 
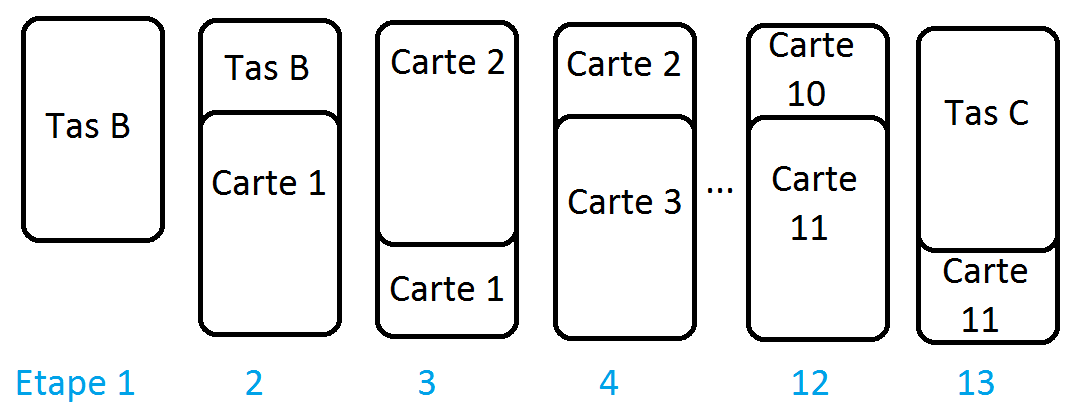
On termine par la carte 11 du tas A, et on recouvre le tout de l'autre tas, ici le tas C.
Nous avons donc nos 32 cartes sur la table, posées - je vous l'accorde - d'une drôle de façon. Prenez le tout d'une main, le pouce sur une tranche, les autres doigts sur l'autre tranche, en veillant à ce que les cartes soient bien serrées les unes contre les autres. Tapez ensuite les cartes sur la table du côté où des cartes dépassent. Si tout se passe bien, alors au moment où les cartes qui dépassaient s'enfoncent, d'autres doivent remonter à leur tour de l'autre côté. Réitérez cette opération de l'autre côté des cartes. Il doit se passer la même chose : en enfonçant ces cartes, d'autres doivent ressortir de l'autre côté. Recommencez jusqu'à ce qu'il ne reste plus qu'une carte. Et là, magie ! C'est le 9 de pique.
-----
Voilà. Le truc, c'est qu'il y a pas de truc. Ça se fait tout seul ! Pas besoin de traficoter les cartes ! L'explication est d'ordre mathématique je pense. En distribuant les cartes et en mettant le tas où se trouve le 9 de pique entre les deux autres tas, et en recommençant ce procédé, je pense que le 9 de pique va se trouver "de plus en plus au milieu de nos 32 cartes" (oui, bon, c'est pas très français !  ).
).
Au bout des quatre distributions de cartes, le 9 de pique se trouvera obligatoirement dans le tas A ou dans le tas B. Comme ces deux tas comportent tous les deux 11 cartes, le 9 de pique se trouvera au milieu : en 6ème position. C'est pour ça qu'au moment de taper les cartes sur la table, c'est le 9 de pique qui ressort à la fin.
-----
J'espère que mes explications auront été assez claires ! Pensez-vous qu'il y ait des nombres de cartes à prendre spécifiques pour que le tour marche ? (J'avais pensé à un nombre de cartes qui soit de la forme 6n+8, n entier naturel. 32 marcherait ainsi avec n=4. Si on prend un n quelconque, même n = 0, on pourrait très bien faire le tour. On aurait 8 cartes, et il suffirait de les distribuer 2 fois pour que notre fameux 9 de pique se retrouve au milieu. Mais là, le tour ne serait pas vraiment impressionnant !  ) En fonction du nombre de cartes, peut-on trouver une formule donnant le nombre de fois où il faudrait faire la distribution des cartes ? Et pensez-vous qu'il y a une manière de placer les tas (le tas C au-dessus plutôt que le tas C en-dessous par exemple ?) réduisant le nombre de distributions de cartes ?
) En fonction du nombre de cartes, peut-on trouver une formule donnant le nombre de fois où il faudrait faire la distribution des cartes ? Et pensez-vous qu'il y a une manière de placer les tas (le tas C au-dessus plutôt que le tas C en-dessous par exemple ?) réduisant le nombre de distributions de cartes ?
Et puis, si quelqu'un a une vidéo youtube du dit tour de magie, qu'il la poste car une petite illustration sera la bienv'nue. 

 Accueil
Accueil
 Forum
Forum







