 |
#1 - 22-10-2011 19:31:15
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
a vous de payrr !
Ash choisit mentalement un nombre [latex]a[/latex] dans {1,2,....,144}.
Mathias qui cherche à découvrir [latex]a[/latex], peut choisir un sous-ensemble[latex] E[/latex] de {1,2,....,144} et demander si [latex]a[/latex] appartient à [latex]E[/latex] ou non.
- Si la réponse de Ash est Oui, Mathias doit payer 2 euros.
- Si la réponse de Ash est Non, Mathias doit payer 1 euros.
Quel est la somme minimale nécessaire que Mathias doit posséder au départ pour être assuré de trouver [latex]a[/latex] ?
Généraliser pour un ensemble de départ de p nombres !
Bonne chance
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#2 - 22-10-2011 20:23:04
- Yuka2
- Habitué de Prise2Tete
- Enigmes résolues : 48
- Messages : 31
A vosu de payer !
Je dirais que Mathias va raisonner par dichotomie mais comme le coût du oui est deux fois plus cher que le coût du non, alors il va séparer à chaque fois son intervalle en 1/3 et 2/3
Ainsi la première question va être :
a est-il entre 1 et 48 (=144/3)
Si la réponse est oui l'intervalle est réduit par 3 pour un coût de 2
Si la réponse est non l'intervalle restant est 2 fois plus grand mais le coût est 2 fois plus faible.
Une petite simulation me donne un coût minimal de 12 pour trouver a à coup sûr.
Une petite formule récursive sous excel me donne :
Soit q = arrondi inf de p/3 et r = arrondi sup de p/3
C(p) = min( max(2+C(q);1+C(1-q)) ; max(2+C(r);1+C(1-r)) )
C(p) = f(ln(x)) agrémenté de quelques arrondi

#3 - 23-10-2011 00:40:56
- fuyuki
- Habitué de Prise2Tete
- Enigmes résolues : 25
- Messages : 13
a vous de payet !
je dirais 16€ ~
on cherche entre 1~>144 un nombre donc on retranche de moitié a chaque fois qu'il appartienne ou pas à l'ensemble car on prend celui complémentaire.
etape 1 : E {1,...,72} au maximum perte de 2€
etape 2 : E {1,...,36} au maximum perte de 2€ -> -4€
etape 3 : E {1,...,18} au maximum perte de 2€ -> -6€
etape 4 : E {1,...,9} au maximum perte de 2€ -> -8€
etape 5 : E {1,...,6} au maximum perte de 2€ -> -10€
etape 6 : E {1,...,3} au maximum perte de 2€ -> -12€
etape 7 : après il reste 3 choix : 1,2 ou 3 (ou encore 3 autres chiffres se suivant) et sachant qu'un mauvais choix = -1€ et qu'il y a 3 choix donc 2*-1=-2€ et que le dernier choix se finit par un -2€ alors -2-2=-4€
et -12-4 = -16€ il faut donc qu'il possède au minimum 16€
mais je ne sais pas du tout comment m'y prendre avec "p" nombres ^^"
#4 - 23-10-2011 08:21:46
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
A vous de payr !
J'aurais envie de dire 12€.
Il vaut mieux séparer en gros l'ensemble en 3 pour 2€ ou en 2/3 pour 1€ que de faire une dichotomie à 16€.
On arriverait , dans le cas général, si P<3^n (n minimum ) à payer 2n+2 €
#5 - 23-10-2011 10:32:44
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
a vous de payrr !
En partant d'un nb d 'éléments de E croissant et en cherchant les meilleurs partages, on tombe sur la suite de Fibonacci.
Avec 144, qui est le 12 ème nombre de Fibo,on doit s'en sortir avec 11 euros.
Plus généralement on aura besoin de k-1 euros pour les nombres <= au kième nb de Fibo.
#6 - 23-10-2011 12:28:16
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
z vous de payer !
Seul Nodgim a la bonne réponse jusqu'à présent.
Pour les autres, il y a mieux à faire , économisez 
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#7 - 23-10-2011 12:47:05
- clement.boulonne
- Passionné de Prise2Tete
- Enigmes résolues : 28
- Messages : 64
a vous fe payer !
On découpe l'ensemble E en deux sous ensembles de même taille (on peut le faire car 144 est divisible par 2).
[TeX]E_1 = \{1,\ldots,72\}[/latex] et [latex]E_2 = \{73,\ldots,144\}[/TeX]
On demande si a est dans E1.
Si la réponse est OUI, on garde le premier ensemble (et on perd 2 euros). Si la réponse est NON, on garde le second ensemble (et on perd 1 euro).
On découpe encore en 2 l'ensemble gardé (72 est divisible par 2) et on demande la même chose que précédement. Si la réponse est OUI, on garde le premier ensemble (et on perd 2 euros). Si la réponse est NON, on garde le second ensemble.
On découpe encore en 2 l'ensemble gardé (36 est divisible par 2) et on demande la même chose que précédement. Si la réponse est OUI, on garde le premier ensemble (et on perd 2 euros). Si la réponse est NON, on garde le second ensemble.
On découpe encore en 2 l'ensemble gardé (18 est divisible par 2) et on demande la même chose que précédement. Si la réponse est OUI, on garde le premier ensemble (et on perd 2 euros). Si la réponse est NON, on garde le second ensemble.
Ensuite il nous reste plus qu'un ensemble à 9 éléments. On le découpe en 3 et on fait demande si a est dans le premier ensemble. Si OUI, on garde le premier ensemble. Sinon, on demande s'il est dans le deuxième ensemble. Si OUI, on garde le deuxième. Si NON, on garde le troisième.
Il nous reste plus qu'un ensemble à 3 éléments et on le divise en 3 (il ne restera plus qu'un élément) et on fait comme précédemment.
Donc si le nombre a = 144, on aura perdu 1+1+1+1+1+1+1+1 = 8 euros...
#8 - 23-10-2011 15:28:52
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
A vous de apyer !
Mathias défigure Ash avec un cure-dents en le traitant de "sale Belge" et lui vole son portefeuille 
Sérieusement, j'ai toujours été nul à ce genre d'énigmes logiques 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#9 - 23-10-2011 18:06:21
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
A vous de payr !
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#10 - 24-10-2011 07:40:59
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
A vous de paer !
Il faut 11€...
Avec l'arbre suivant, on peut voir que n€ permettent de trouver le nombre parmi F(n+1) nombre où Fn est le n-ème terme de la suite de Fibonacci originalement revisitée.
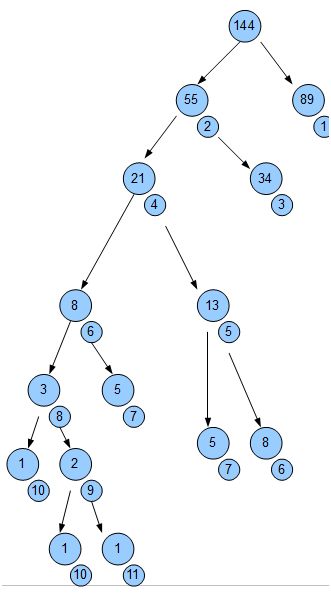
11€ : 144
12€ : 233
13€ : 377
...
#11 - 24-10-2011 13:35:19
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
a vpus de payer !
Bravo gwen Félicitation 
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#12 - 24-10-2011 18:05:12
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
A vous de payr !
Il devrait pouvoir s'en sortir avec 11 euros au départ.
Plus généralement, si le nombre est dans 1..p:
On note S la suite telle que S0 = 2 et Sn+1 = Sn + Fn; où F est la suite de Fibonacci
(pour rappel, F0 = F1 = 1, Fn+2 = Fn+1 + Fn)
S0 = 2
S1 = 3
S2 = 4
S3 = 6
S4 = 9
S5 = 14
S6 = 22
etc...
Si Sn <= p < Sn+1; alors il faut n+2 euros pour trouver le nombre cherché.
La démo complète viendra si j'ai le temps (j'en doute).
En deux mots cependant: soit Un la suite telle que Un est le nombre d'euros nécessaires pour p=n
- U2 = 2 (au moins une question; et une chance de payer la "grosse" réponse)
- U(n+1) = min[i=1..n+1, max[2+ U(i); 1+ U(n+1-i)]]
Explication : à i fixé, je choisi un intervalle de taille i (et un autre de taille n+1-i implicitement). Si la réponse est dans mon intervalle, je paye 2 et je suis réduit à un intervalle de taille i (d'où 2 + Ui); sinon je paye 1 et je suis réduit à un intervalle de taille n+1-i (d'où le U(n+1-i)).
Comme je ne choisis pas ce qui va arriver, je suis obliger de prendre le max des deux valeurs. Par contre, je peux tout à fait choisir ensuite le i le plus accommodant (celui qui minimise le max)
#13 - 24-10-2011 18:33:20
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
A vous de payr !
Et bravo Scarta ! Excellent 
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#14 - 24-10-2011 19:22:00
- patouu
- Habitué de Prise2Tete
- Enigmes résolues : 48
- Messages : 26
#15 - 24-10-2011 19:55:51
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
A vous de pyaer !
non un peu moins 
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#16 - 24-10-2011 22:50:49
- patouu
- Habitué de Prise2Tete
- Enigmes résolues : 48
- Messages : 26
Avous de payer !
Ben oui, 13€, car pour la dernière, avec 1€, il saura!
#17 - 25-10-2011 02:16:10
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
A vous d payer !
on a besoin de 11 euros.
Pour 144 on commence par donner un sous ensemble de 144/((3+√5)/2) soit 55 elements
si il dit oui, on a 55 elements restant si non il en reste 89
sur les 89, on donne un sous ensemble de 34 elements, qui nous donne soit 34 elements avec un cout de 3 ou 55 avec un cout de 2. On generalise:
144 coute 0
89 coute 1
55 coute 2
34 coute 3
21 coute 4
13 coute 5
8 coute 6
5 coute 7
3 coute 8
2 coute 9
1 coute 10 si on vient de 3
ou 10 ou 11 si on vient de 2
Donc le maximum dont on a besoin est 11.
Je pense qu'on peut generaliser avec pour un nombre de depart N:
on a besoin de INT (2 * ln (N)÷ ln ((3+√5)/2))+1 euros. (INT etant la partie entiere du nombre)
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#18 - 25-10-2011 03:08:57
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
A voous de payer !
Patou : il y a encore mieux à faire !
Bonne réponse de dhrm77
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#19 - 25-10-2011 10:23:05
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
a vous fe payer !
Formule plus simple: F est la suite de Fibonacci toujours, et si
F(n) + 1 <= p <= F(n+1); alors la réponse est n+1
(Ben oui, la somme des termes de la suite de Fibonacci peut aussi s'exprimer sous la forme d'un nombre de Fibonacci). Du coup, je pense qu'à démontrer, ça doit être plus simple
Exemple ici: F(10) = 89; F(11) = 144 donc comme 90 <= 144 <= 144; la réponse est 11
#20 - 25-10-2011 20:14:06
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
A vos de payer !
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#21 - 26-10-2011 20:11:26
- nicolas647
- Passionné de Prise2Tete
- Enigmes résolues : 24
- Messages : 96
A vosu de payer !
Pas réussi à trouver de formule générale, mais je peux dire que la proportion de nombres à prendre dans le sous-ensemble doit s'approcher de 1/3.
Par contre je pense avoir trouvé un algorithme pour trouver la réponse, que j'ai mis en œuvre dans un tableur.
Pour p=144, ma réponse est 12.
#22 - 26-10-2011 20:13:15
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
A vouus de payer !
nicolas647 : tu es tout proche , un peu moins ! tu peux économiser 
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#23 - 26-10-2011 21:34:08
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
a vius de payer !
Il suffit de trouver [latex]x[/latex] le nombre d'itération ou l'on divise le nombre d'élément par 2 pour se retrouver avec un seul et unique [latex]p_i[/latex]
On résout donc :
[TeX]\frac{p}{2^x}=1[/latex] donne [latex]x=\frac{-ln(\frac{1}{p})}{ln(2)}[/latex] avec [latex]\frac{1}{p}>0[/TeX]
Avec [latex]p[/latex] éléments il faudra payer [latex]x[/latex] euros soit avec 144 éléments [latex]\fbox{x=\frac{2.ln(12)}{ln(2)}=7.1699...}[/latex] donc 8€
Shadock  (En espérant ne pas avoir dit de bêtises) (En espérant ne pas avoir dit de bêtises)
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#24 - 26-10-2011 21:42:04
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
a vous de pzyer !
shadock: je crains que ta somme n'est pas suffisante à Mathias pour être sur de trouver [latex]a[/latex]
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#25 - 26-10-2011 23:34:54
- nicolas647
- Passionné de Prise2Tete
- Enigmes résolues : 24
- Messages : 96
a vous de pauer !
Effectivement j'avais oublié des possibilités, la somme minimale est de 11. Il faut prendre un premier sous ensemble de 55 éléments, après c'est en fonction des réponses de Ash.
Toujours pas capable de donner de formule générale...
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







