 |
#1 - 24-02-2012 15:00:57
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Cnocours Griego 3&4
J'annonce le concours Griego ouvert!
Il y a 2 parties dans la section mathématiques et 1 partie dans la section logique.
Il y a 2 questions par parties, car vous devez au moins répondre à 4 questions pour faire parti du concours.
Vous indiquerez vos réponses sous forme claire, sans mélanger les 2 problèmes.
1-Dans ce triangle découpé, on a mis les chiffres de 1 9. Puis on a additionné certains nombres et affiché leur somme dans les rectangles. (Exemple : le 28 est l’addition des 5 chiffres dans les triangles du bas, le
27 Est la somme des 5 triangles à droite.)
Quel chiffre se trouve dans la case rouge, au maximum ? 
2-Dans le cryptarythme ABCD-DCBA, on a trouvé le résultat maximum de l’opération et le résultat minimum. Les deux sont tous des nombres entiers, non nul et positifs. A,B,C,D représentent tous des nombres différents, sauf 0.
Quel est le résultat minimum, et le résultat maximum ?
Un promath- actif dans un forum actif
#2 - 24-02-2012 16:40:04
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Concours Grriego 3&4
Provisoirement (je me réserve le droit d'améliorer mon score  ) je trouve : ) je trouve :
1- 7
2 - 2087 et 279
#3 - 24-02-2012 21:03:37
- MacArony
- Passionné de Prise2Tete
- Enigmes résolues : 49
- Messages : 52
- Lieu: Liège
Concours Griego 3&apm;4
Plus facile à résoudre que à expliquer 
Bon j'essaye...
1) Si on considère que le maximum est 9,
On doit donc placer le 8 sur le triangle orange :
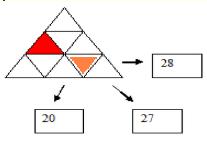 , ,
En effet, ce triangle est à l'intersection des 3 sommes.
Si le 8 n'était pas placé là, on aurait au maximum 7+6+5+4+3 = 25; or on doit arriver à 27 et 28, le 8 doit donc servir pour les deux.
Pour obtenir 20 en 3 cases, on ne peut utiliser que 875 (2 combinaisons avec le 8 au milieu)
Mais aucune de ces 2 combinaisons ne satisfont 27 et 28.
Si on considère un maximum de 8
Le 9 est placé sur le triangle orange, comme expliqué ci-dessus et donc pour obtenir 20, on a le choix entre les combinaisons 974 et 965.
Mais encore une fois, aucune des ces 4 ne satisfait les sommes.
Si on considère un maximum de 7
Cela semble marcher, voici une solution :
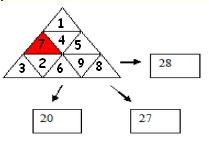
2) Pour trouver le résultat maximum, c'est facile, il faut A et B les plus grands possible avec A>B et C et D les plus petits possible avec C<D
Ce qui donne 9821 - 1289 = 8532
Pour le résultat minimum, j'ai procédé en tâtonnant.
AB et DC ainsi que ABCD et DCBA doivent être fort proches avec A>D>B et C le plus grand possible.
J'ai donc 6 possibilités :
3192-2913 ; 4193-3914 ; 5194-4915 ; 6195-5916 ; 7196-6917 et 8197-7918 pour un résultat de 279
Voila voila 
Mac
Chien qui court dans la cour ne mérite aucun discours, mais lion qui accourt sans recours, au secours !
#4 - 24-02-2012 22:34:45
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
concours griego 3&zmp;4
Exo 1:
http://www.prise2tete.fr/upload/gilles355-EXO01.jpg
Dans le lien ci-dessus on trouve une soution avec la case rouge = 7.
Démontrons pourquoi il est impossible que la rouge = 9 :
Voici la liste des additions à 3 chiffres différents donnant 20 :
5+6+9
4+7+9
3+8+9
7+5+8
On serait donc obligé de prendre 7+5+8=20 car le 9 est pris par la case rouge.
Mais dans ce cas, même en mettant en toute logique 6 en bas à droite on aurait la situation du lien ci dessous.
http://www.prise2tete.fr/upload/gilles355-EXO011.jpg
Les chiffres restant étant 1,2,3 et 4 nous devons faire 8 et 8 soit 16 or 1+2+3+4=10.
Démontrons qu'il est impossible que la rouge = 8 :
En reprenant la liste des 3 chiffres faisant la somme de 20, on aurait 2 possibilités 5+6+9 et 4+7+9 car le 8 est pris par la case rouge.
Que l'on prenne l'une ou l'autre des situations on se retrouve encore avec des sommes impossibles à réaliser avec les chiffre 1,2,3 et 4 en mettant le plus gros chiffre restant en bas à droite bien entendu (7 dans le premier cas et 6 dans le second).
La solution est donc 7 puisque nous avons vu une solution possible (1er lien) avec ce chiffre en case rouge.
Exo 2:
J'ai bien entendu pris l'hypothèse que A,B,C et D était des chiffres et non des nombres différents de 0 
ABCD-DCBA= 1000A+100B+10C+D-1000D-100C-10B-A
= 1000(A-D)+100(B-C)+10(C-B)+(D-A)
= 999(A-D)+90(B-C)
a)Pour le résultat maximum il faut que A-D soit le plus grand possible car il est multiplié par 999 et que B-C soit donc le second plus grand possible car 90 est moins important que 999.
On prend donc A=9, D=1, B=8 et C=2 ce qui nous donne 9821-1289 = 8532
b)
ABCD-DCBA = 999(A-D)+90(B-C)
= 999(A-D)-90(C-B)
Nous avons vu que le plus grand écart possible est 9-1=8, or 90*8=720 qui est plus petit que 999.
A-D ne peut donc pas être négatif, nous prendrons donc A-D=1 (écart le plus petit possible en restant entier positif).
Par contre il faut que l'écart entre C et B soit lui le plus grand possible.
On prend donc C=9, B=1 puis pour A et D nous avons plusieurs solutions étant respectivement (A=3 et D=2),(A=4 et D=3), (A=5 et D=4), (A=6 et D=5), (A=7 et D=6) et (A=8 et D=7)
ce qui donne : 999-720= 279 que l'on trouve en faisant les opérations telles que :
3192-2913 = 279
4193-3914 = 279
5194-4915 = 279
6195-5916 = 279
7196-6917 = 279
8197-7918 = 279
Voilà et encore merci pour ces petites énigmes bien sympathiques.
#5 - 24-02-2012 23:50:29
- Greg02
- Amateur de Prise2Tete
- Enigmes résolues : 14
- Messages : 5
concours gtiego 3&4
Et bien je dirais que la réponse est le 9. Mais sans grande conviction ^^
#6 - 25-02-2012 01:35:05
- Grizix
- Habitué de Prise2Tete
- Enigmes résolues : 30
- Messages : 31
oncours Griego 3&4
1 - De gauche à droite, du haut vers le bas (sens de lecture), les valeurs sont A, B, C, D, E, F, G, H, I. On cherche à maximiser B sachant que :
A+C+D+H+I = 27
E+F+G+H+I = 28
G+H+D = 20
A+B+C+D+E+F+G+H+I = somme(1-9) = 45
A+B+C+D+E+F+G+H+I = (A+C+D+H+I) + (E+F+G+H+I) + B - H - I
Donc 45 = 27 + 28 + B - H - I <=> B = H + I - 10
B est maximal pour (H+I) maximal, càd H+I = 9+8 = 17 et B = 7.
On vérifie qu'il existe un solution :
Si H = 8, G+D = 12 donc G=D=6 (car 7, 8 et 9 déjà utilisés) => impossible.
Donc H = 9, I = 8, B = 7.
G+D = 11 = 6+5 (seule possibilité).
À partir de là, plusieurs solutions :
A = 1, C = 4, D = 5, E = 2, F = 3, G = 6 ;
A = 2, C = 3, D = 5, E = 1, F = 4, G = 6 ;
A = 1, C = 3, D = 6, E = 2, F = 4, G = 5 ;
On peut de plus permuter A avec C et E avec F à chaque fois, donc 6 solutions au total pour maximiser B à 7.
2 - Pour le maximum, il faut commencer par maximiser le chiffre des milliers, donc 9-1, puis maximiser le chiffre des centaines, donc 8-2.
MAX : 9821 - 1289 = 8532
Pour le minimum, il faut commencer par minimiser le chiffre des milliers. Le résultat doit être positif, donc on aura forcément une différence de 1 au minimum sur le chiffre des milliers.
Ensuite, on minimise le chiffre des centaines. Comme on sait qu'on a déjà au moins un millier dans la vue, on peut faire du négatif avec les centaines, donc 1-9.
On a donc, avec x = y+1 :
MIN : x19y - y91x = 279
#7 - 25-02-2012 02:14:27
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
Concours Griego 3&
1. Le chiffre de la case rouge est au maximum 7, comme dans l'exemple suivant :
2. Le résultat minimum est 279 avec 3192 - 2913 et le maximal est 8532 avec 9821 - 1289.
Si les résultats doivent n'être composés que des chiffres A, B, C et D, on a comme minimum 459 (DAC) avec 5394 - 4935 et 6174 (BDAC) avec 7641 - 1467.
#8 - 25-02-2012 04:28:14
- emerald000
- Amateur de Prise2Tete
- Enigmes résolues : 44
- Messages : 7
concours grirgo 3&4
1- 7
2- Minimum: 279
Maximum: 8532
#9 - 25-02-2012 09:52:36
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
concours gruego 3&4
Pour la première, j'appelle X la valeur demandée, et a et b les chiffres des deux cases en bas à droite communes au sommes 27 et 28.
Si je fais la somme de tous les chiffres de la pyramide, je dois avoir 1+2+...+9=45
si j'ajoute les chiffres de la ligne 28 et de la ligne 27, ça me donne tous les chiffres de la pyramide, sauf le X, mais avec en double les a et b
J'obtiens donc : 28+27=45+a+b-X, c'est à dire :
X+10=a+b
Je veux trouver Xmax. 9 et 8 sont exclus, Xmax est donc 7.
Il reste à trouver une configuration qui fonctionne pour valider aussi la ligne dont la somme fait 20 :
--1--
-745-
32698
La réponse est donc 7
Pour le second problème, je trouve pour résultat maxi :
9821-1289=8532, et pour mini :
3192-2913=279
#10 - 25-02-2012 16:27:02
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
convours griego 3&4
Question 1
Montrons que le chiffre de la case en rouge peut atteindre mais ne peut pas dépasser 7.
a/ En appelant a,b,c,d,e,f,g,h,i les chiffres des cases en partant du haut, et de gauche à droite, on a les relations :
(1)a+c+d+h+i=27
(2)g+d+h=20
(3)e+f+g+h+i=28
Et aussi
(4)a+b+c+d+e+f+g+h+i=45 (somme des chiffres de 1 à 9)
En faisant (4)-(1), on obtient :
(5)b+e+f+g=18
Puis (3)-(5) :
(6)h+i-b=10
On a donc b=h+i-10
Comme h+i ne peut pas dépasser 17, b ne peut pas dépasser 7.
b/ Voici une configuration où b=7 :
Question 2
La différence des 2 nombres vaut :
1000A+100B+10C+D - 1000D+100C+10B+A = 999(A-D) + 90(B-C)
a/Pour le maximum
Il faut maximiser A-D et B-C. La valeur maximale est 8 (9-1), mais ne peut pas être utilisée pour les 2. On a intérêt à privilégier A-D, car 8*90 < 999.
On prend donc A-D=8, avec A=9 et D=1
B-C peut ensuite valoir au maximum 6, avec B=8 et C=2
Ce qui donne 9821-1289=8532
Le résultat maximum est donc 8532
b/Pour le minimum
A-D ne peut être nul, car les chiffres sont différents.
A-D ne peut pas être négatif, car alors la différence serait négative, l'énoncé l'interdit
Il nous reste A-D=1
Ensuite, on peut prendre B-C=-8, le résultat restera positif. Avec donc B=1 et C=9.
On peut prendre ce qu'on veut pour A et D tant que A-D=1
Ce qui donne par exemple 3192-2913=279
Le résultat minimum est donc 279
#11 - 25-02-2012 16:35:25
- fred101274
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 163
- Lieu: devant mon écran
Concours Griego 3&4;
Pour le 1, la réponse est 7. Une solution serait alors de haut en bas et de gauche à droite : 3 7 2 5 1 4 6 9 8. En plaçant 8 ou 9 dans la ces rouge et en mettant les deux plus grands chiffres restant dans les 2 en bas à droite, il ne reste pas assez pour obtenir 27 et 28...
Pour le 2, je cherche encore...

On n’est jamais très fort pour ce calcul...
#12 - 25-02-2012 18:21:10
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
oncours Griego 3&4
Griego 3
Le chiffre maximum pouvant se trouver dans la case rouge est 7 .
Montrons que l'on ne peut pas avoir 9 dans le triangle rouge.
En effet dans ce cas la somme des nombres des autres triangles serait [latex]\ge 28+27-8-7 =40[/latex] .
Donc [latex]1+\cdots+9 \ge 9+40[/latex], c-à-d [latex]45\ge 49[/latex], contradiction.
Montrons que l'on ne peut pas avoir 8 dans le triangle rouge.
En effet dans ce cas la somme des nombres des autres triangles serait [latex]\ge 28+27-9-7 =39[/latex] .
Donc [latex]1+\cdots+9 \ge 8+39[/latex], c-à-d [latex]45\ge 47[/latex], contradiction.
On peut avoir 7 dans le triangle rouge comme le montre la solution
2
7 3 5
1 4 6 9 8
Griego 4
Je suppose que A,B,C,D sont des chiffres différents.
résultat minimum 279
résultat maximum 8532
3192 - 2913 = 279
9821 - 1289 = 8532
#13 - 25-02-2012 21:58:02
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
concours gruego 3&4
1.
2.
- La différence peut s'écrire 999(A-D)+90(B-C)
- Je maximise (en priorité vu son coefficient) A-D avec 9-1 = 8 puis B-C avec 8-2=6 soit 8532
- Je minimise A-D avec, par exemple, 9-8=1 (pas moyen de faire mieux avec des naturels différents) et B-C avec, par exemple, 7-6=1 soit 1089
#14 - 26-02-2012 09:59:06
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
concours griego 3&amo;4
Je vois que ce concours a du succès.
Bravo à tous!
Voici les réponses:
1-7
2-279;8532
Un promath- actif dans un forum actif
Sujets similaires
| Sujet |
Date |
Forum |
|
|
02-11-2011 |
Enigmes Logiques |
|
|
11-04-2019 |
Enigmes Logiques |
|
|
12-04-2011 |
Enigmes Logiques |
|
|
25-01-2011 |
Enigmes Logiques |
Une suite très étrange 0, 0, 1, 1, 2, 2, 3, 3, 4, 0, 0, 1, 1 par MMORgan
|
21-01-2010 |
Enigmes Logiques |
|
|
16-05-2011 |
Enigmes Logiques |
|
|
11-07-2009 |
Enigmes Logiques |
|
|
19-06-2009 |
Enigmes Logiques |
|
|
17-03-2009 |
Enigmes Logiques |
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







