 |
#26 - 10-01-2013 21:44:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
au moins lz moitié !
J'oubliais , un immense merci au ch'Ef de nous avoir rendu Latex 
Vasimolo
#27 - 10-01-2013 22:17:45
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
au moins la moutié !
Vasimolo a écrit:A dire vrai je n'ai pas regardé ta théorie en détail , le nombre de point étant fixé , si on peut faire plus que 1 en acceptant les contacts , on peut faire plus que 1 en les approchant , c'est une évidence topologique 
Vasimolo
Donc tu crées une variable (que j'appelerais "tolérance de vide entre deux rectangles" = X) que tu fais tendre vers 0 pour valider l'énoncé du problème.
Moi, je propose un nouvel énoncé
Dans un carré d'aire 2 avec comme premier point le coin en bas à gauche du carré.
Démontrer que pour toute valeur de X > 0, il existe un nombre de point a partir duquel il est impossible de construire dans le carré des rectangles disjoints dont le coin inférieur gauche est l'un des points donnés et tel que la somme de leurs aires soit supérieure à 1 .
#28 - 10-01-2013 22:34:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
zu moins la moitié !
Je ne vois pas trop ce qu'est ton "X" . Il est clair que pour toute valeur de X même très petite on peut trouver un exemple où le recouvrement d'aire 1+X n'est pas possible , mais ça ne contredit en rien ce que je dis 
Vasimolo
#29 - 11-01-2013 00:24:19
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
au moins la moutié !
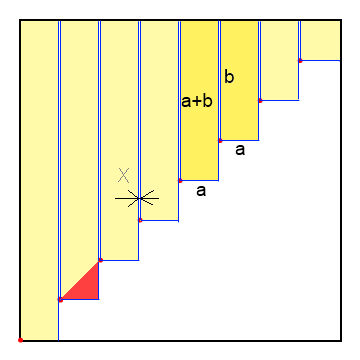
Je reprends le dessin de Jackv pour definir X.
En gros, tu nous dis, quelque soit le nombre de point, il y a aura une valeur de X qui permettra le pavage d'une aire supérieure à 1.
Alors que moi, je dis que pour tout X, il y aura un nombre de point qui ne permettra pas le pavage d'une aire supérieure à 1.
Les deux phrases sont vraies ...
#30 - 11-01-2013 18:11:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
au moins ka moitié !
Bon d'accord je vois ce que tu veux dire 
Tu fixes [latex]X[/latex] puis tu augmentes [latex]n[/latex] alors que je fixais [latex]n[/latex] avant de diminuer [latex]X[/latex] ( ce qui semble plus naturel pour le problème ) .
Sinon , comme tu le dis , les deux affirmations sont vraies .
Vasimolo
#31 - 11-01-2013 18:20:32
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Au moins al moitié !
Encore une fois, le dessin de jackv n'est pas représentatif du problème posé. Ce n'est qu'un aspect particulier.
#32 - 13-01-2013 11:06:47
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
au moind la moitié !
Indépendamment de la démonstration complète, on peut s'amuser à chercher la surface maximale perdue avec 2 pts, 3pts...
Pour 1 point (celui en bas à gauche) la surface perdue=0
Pour 2 pts, la surface perdue max est =1/4
Pour 3 pts ?
Je n'ai pas encore tenté pour 4 pts.
#33 - 13-01-2013 11:14:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
au moins la loitié !
Il me semble qu'on a déjà émis l'hypothèse [latex]\frac{n-1}{n}[/latex] pour un carré d'aire 2 , mais sans preuve bien entendu 
Vasimolo
#34 - 13-01-2013 11:56:31
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
au moibs la moitié !
Si je comprends bien l'hypothèse, si n=3, (2/3)*(1/4)=1/6 de la surface totale ?
Bah...
#35 - 13-01-2013 13:09:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Au moins la motiié !
Si [latex]n=3[/latex] 
Surface totale : [latex]2[/latex]
Surface perdue : [latex]\frac{2}{3}[/latex]
Fraction perdue : [latex]\frac 13[/latex]
Vasimolo
PS : j'avais noté côté 2 au lieu d'aire 2 , c'est peut-être la raison de la méprise 
#36 - 13-01-2013 15:00:33
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
au moins la moiyié !
Là d'accord. Avec les point sur la diagonale.
Pour les points éloignés de la diagonale (placés symétriquement de part et d'autre) j'ai trouvé une perte de 8/27, donc moindre que 1/3.
Je comprends bien la tentation de l'utilisation de la récurrence, mais....
#37 - 14-01-2013 11:21:00
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
Au moins la mitié !
Pour le moment, il n'y a aucun exemple pour démontrer que la diagonale n'est pas le cas le plus défavorable (pour un nombre de point définit)
Comme pour ce cas particulier, on a toujours plus de la moitié de la surface pavée, est-ce que le problème revient à prouver qu'il n'y a pas meilleur placement que les points sur la diagonale ?
#38 - 14-01-2013 19:06:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Au oins la moitié !
Oui, c'est exactement le problème. La récurrence est malheureusement ici une démonstration insuffisante: Ce n'est parce qu'on a optimisé avec n points qu'il faut partir de cette configuration à n points pour fabriquer la configuration optimale à n+1 points.
#39 - 15-01-2013 15:36:26
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Au moinns la moitié !
Salut !
J'ai une petite idée à vous soumettre...
J'appelle maillage d'un rectangle de taille n, un découpage régulier du rectangle en n petits carrés. Il est simple, par récurrence forte , de montrer que pour tout maillage de taille n tels que tout les points proposés soient situés sur des coins des petits carrés et dont un est en bas à gauche, on peut faire des rectangles tels que la somme des aires est plus grande que 1/2 de l'aire du rectangle. On passe à la récurrence en utilisant le point le plus proche du coin en bas à gauche, au sens suivant, le point dont le maximum entre l'abscisse et l'ordonnée est minimal. En effet, le rectangle en haut à droite de ce point vérifie l'hypothèse de récurrence, et la zone égale au rectangle de départ privé de ce nouveau rectangle peut être couverte par plus de la moitié de sa surface à cause de la propriété du point : on fait le rectangle vers la droite ou le haut selon lequel occupe le plus de place. Pour finir on fait un maillage tel que tous les points soient sur un des coins des petits carrés.
Désolé si c'est peu clair et\ou faux.
Un mathématicien complet est topologiquement fermé!
#40 - 15-01-2013 15:56:29
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
A moins la moitié !
Salut.
Ta définition du point "le plus proche du coin en bas à gauche" a l'air bancale.
Précise-la un peu plus.
Ensuite, il faut prouver que tu peux couvrir la moitié de la zone égale au rectangle de départ privé de ce nouveau rectangle, et là tu ne donnes pas beaucoup d'explications.
#41 - 15-01-2013 16:06:28
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
au moins lz moitié !
C'est le point le plus proche pour la distance D(A,B)=Max(|xA-Xb|,|yA-yB|).
Ensuite il faut considérer les deux rectangles de la "zone" auquels on applique la récurrence un peu "plus loin" si il y des points et on prend l'espace sinon plus le carré, je sais que c'est pas clair du tout et j'ai des doutes... Mais ça peut donner des idées.
Un mathématicien complet est topologiquement fermé!
#42 - 15-01-2013 16:29:59
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Au moins la mmoitié !
Prenons un carré 8x8, avec les points (2,2), (4,1), (1,4), et d'autres points plus en haut et à droite de ces 3 là.
Tu vois que ton raisonnement ne s'applique pas :
La carré fait 64 de surface donc il faut en couvrir 32.
Tu prends le rectangle en haut et à droite de (2,2) pour appliquer ton HR : tu obtiens 18. De même, tu appliques l'HR avec les deux rectangles en haut et à droite de (4,1) et (1,4) : tu obtiens 4. Total : 22, et du coup il manque 10 à trouver avec un rectangle de coin (0,0) : impossible, on fait 8 au max.
#43 - 15-01-2013 18:01:15
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
au moind la moitié !
J'ai déja tenté le quadrillage, en vain.
#44 - 15-01-2013 18:23:51
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
u moins la moitié !
ok, le problème est très sympa...
Un mathématicien complet est topologiquement fermé!
#45 - 15-01-2013 18:31:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Au moins la moité !
Attention , c'est addictif 
Vasimolo
#46 - 15-01-2013 18:52:09
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
au moins la miitié !
Je cherche aussi à l'aide d'un quadrillage, mais sans qu'il soit pour autant régulier.
Je suis sur une approche différente, je vous la livre pour idée...
Je commence avec un seul point, en bas à gauche, et donc mon carré est entièrement plein.
Ensuite je place un point dans le carré, qui, au lieu d'ajouter un rectangle comme dans l'énoncé, me fait enlever un rectangle, soit en haut à gauche, soit en bas à droite, et j'avance ainsi pas à pas en ajoutant des points un à un.
Si j'ajoute un point dans une zone vide, il me rajoute un rectangle. S'il est dans une zone remplie, il m'enlève un peu d'aire.
Une idée parmi les vôtres...
#47 - 15-01-2013 19:03:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
au loins la moitié !
Là je n'y crois pas trop , mais comme rien ne marche , pourquoi pas 
Vasimolo
#48 - 15-01-2013 19:58:52
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
au mouns la moitié !
Pour avoir le maximum de vide, j'ai l'impression que toutes les coordonnées X de chaque point ainsi que toutes les coordonnées Y doivent être différentes.
Tout point supplémentaire permettrait de mieux pavé le carré.
En fait, ce point supplémentaire ne peut générer plus de vide que s'il n'était pas là.
Au final, cela nous ramenerait à mettre tous les points sur la diagonale !
#49 - 15-01-2013 22:39:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Au moins lla moitié !
Il me semble qu'on peut même considérer que les points sont aux sommets d'un quadrillage orthonormé , ce n'est pas plus simple pour autant 
Vasimolo
#50 - 16-01-2013 01:06:43
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
Au moins la motiié !
Pour illustrer mon propos ci dessus.
Prenons un carré 10 * 10
A(0;0)
B(1;1) par exemple
tout point en (0;X) ou en (X;0) soit bridera le rectangle A mais permettra de faire le complement (et potentiellement faire mieux) soit ne le bridera mais permettra de pavé une autre zone.
Quelque soit l'emplacement de B, le point C ne doit pas avoir une coordonnée commune avec A.
Je pense que cette règle est vraie pour tous les points, donc le cas le plus défavorable reste de mettre tous les points sur la diagonale.
Comme le nombre de point est défini, je pourrais toujours pavé plus de la moitié du carré !
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum






