|
#1 - 29-08-2011 21:00:39
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Ue fonction à moitié continue partout
Bonjours à tous,
Cette fois il faut trouver une bijection de R sur R, discontinue (à gauche) en tout nombre décimale mais continue partout ailleurs.
Quelques indices :
1) Spoiler : [Afficher le message] Rappel: Une fonction f :R->R est continue en a si :
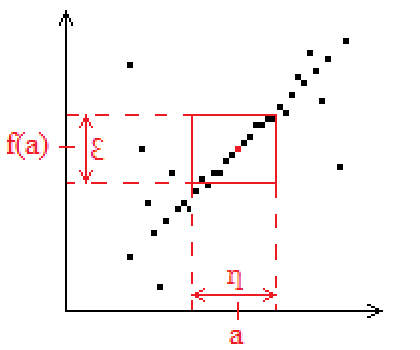
Quel que soit ε>0 il existe η>0 tel que quel que soit x∈]a−η,a+η[ on a f(x)∈]f(a)−ε,f(a)+ε[.
2) Spoiler : [Afficher le message] Si sa définition est vraiment élémentaire, montrer la propriété recherchée est plus délicat.
3) Spoiler : [Afficher le message] Je suis tombé sur cette fonction en jouant avec les décimales des nombres
4) Spoiler : [Afficher le message] f(f(x))=x Oui, ça aide pas beaucoup 
5) Spoiler : [Afficher le message] Si on écrivait un nombres avec des petites tablettes de buis présentant chacune un nombre de 0 à 9 ou une virgules, je pense que la Esméralda pourrait facilement dresser Djali sa chèvre à construire l'image de ce nombre.
#2 - 29-08-2011 22:00:10
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Une fonction à moitié continue prtout
L'idée du titre est que dans n'importe quel intervalle, la fonction est continue en un nombre infinie de points mais aussi discontinue en un nombre infinie de points, et ça, ça peut paraitre paradoxale à première vue, d'où le terme "moitié continue".
#3 - 29-08-2011 22:19:29
- clement.boulonne
- Passionné de Prise2Tete
- Enigmes résolues : 28
- Messages : 64
Un fonction à moitié continue partout
De but en blanc, je dirais 1D qui est la fonction indicatrice sur les nombres décimales. Elle vaut 1 quand x est un nombre décimal et 0 partout...
#4 - 29-08-2011 22:28:56
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Une fonction à moitié continue partouut
clement.boulonne : la fonction indicatrice sur les nombres décimales n'est pas une bijection, et en plus elle n'est continue nulle part. Bien essayé 
#5 - 29-08-2011 22:58:46
- clement.boulonne
- Passionné de Prise2Tete
- Enigmes résolues : 28
- Messages : 64
Une fonction à moitié continue partotu
Ah oui, bijection... C'est corsé d'un seul coup ! 
Une autre proposition. Soit x∈R, je note xD le nombre décimal le plus proche de x.
Soit ε∈R strictement positif, je définis tout d'abord la fonction f sur tous les nombres décimaux : f(x)=x+ε
Ensuite si x est un réel compris entre deux décimaux (je rappelle que D est dense dans R) alors je définis f en x par : f(x)=f(xD)+x=xD+ε+x.
Alors f serait continue sur les nombres réels non décimaux et les sauts se feront sur les nombres décimaux. Par contre, pas sûr qu'elle soit bijective (après mûres rélexions)
Bon, c'est juste une rapide rédaction de mes idées et ça doit être peu clair pour le correcteur...
#6 - 29-08-2011 23:07:13
- esereth
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 176
Une fonction à moitié continue patout
Bonsoir,
Je pense à truc du style :
f(x)=1−x si x est décimal et
f(x)=x sinon.
Elle est bijective mais pour la continuité, je laisse des plus compétents que moi s'en occuper  et vraisemblablement me prouver que je suis dans l'erreur et vraisemblablement me prouver que je suis dans l'erreur  . .
#7 - 30-08-2011 10:08:22
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Une fonction à moitié continue partuot
clement.boulonne : attention le nombre décimale le plus proche d'un nombre non décimale n'existe pas ! Quel que soit celui proposé on peut en trouver un plus proche en lui rajoutant des chiffres à la fin.
esereth :
f(x)=1−x si x est décimal et
f(x)=x sinon.
C'est déjà pas mal pour la bijection, par contre effectivement la fonction n'est continue nulle part (sauf en 1/2 quand 1-x=x)
Spoiler : [Afficher le message] Si la fonction fait des sauts au niveau des nombres décimaux, ces sauts doivent être de plus en plus petit "en se rapprochant des nombres non décimaux" pour assurer la continuité.
#8 - 30-08-2011 10:45:30
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Une fonction à moitié continue partoout
Pour la partie discontinue à gauche : Je ne sais pas trop à vrai dire parce que c'est vraiment trop compliqué mais je tente avec :
f(x)=∞∑n=0an.cos(bnπx)[/latex]avec[latex]0<a<1
Pour la partie continue à droite :(E):\ \left{\frac{sin(x)}{x} \text{ si } x \in \mathbb{R} \\ f(0)= 1 \right qui est continue en 0
Shadock 
PS : Je pense qu'il existe plus simple notamment avec la fonction partie entière.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#9 - 30-08-2011 13:13:05
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Une fonction à motié continue partout
Bonjour,
J'ai mal à la tête, mais je n'ai pas la solution: 
Frank
#10 - 30-08-2011 22:14:19
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
une fonction à mootié continue partout
Hop ! J'ai rajouté un cinquième indice pour les bossus des math 
#11 - 30-08-2011 22:18:02
- clement.boulonne
- Passionné de Prise2Tete
- Enigmes résolues : 28
- Messages : 64
Une fonction à moitié continue prtout
Va falloir que je révise mes notions de Topologie : le CAPES approche !! 
#12 - 31-08-2011 14:01:36
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Une fonciton à moitié continue partout
Les nombres décimaux sont dénombrables, soientt ...d−2,d−1,d0,d1,d2,.... ces nombres je définis f(x)=x si x n'est pas décimal et f(di)=di+1 sinon.
Un mathématicien complet est topologiquement fermé!
#13 - 02-09-2011 20:57:52
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Une fonction à omitié continue partout
#14 - 04-09-2011 18:45:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Une foncton à moitié continue partout
Suis-je le seul à ne pas être convaincu par les solutions proposées ???
Vasimolo
#15 - 04-09-2011 18:47:04
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Une fonction à moitié contiune partout
Moi même ma réponse je ne la comprends pas alors... 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#16 - 04-09-2011 18:57:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Une fonction à moitié continue aprtout

On voit mal en quoi le caractère décimal intervient par exemple par rapport à 1/3=0,3333333...
Vasimolo
#17 - 05-09-2011 00:27:21
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Une fonction à moitié ccontinue partout
... qui n'est pas un décimal :-)
#18 - 05-09-2011 11:11:07
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
une fonctiob à moitié continue partout
Avant de pouvoir donner un avis (car la question m'intéresse) j'aurais besoin de voir une définition précise de la fonction.
On permute les décimales de quoi au voisinage de quoi?
Parce que la c'est trop flou pour qu'on puisse même se faire une idée de la solution proposée.
Je ne suis pas du tout convaincu pour le moment.
Que prend-on pour les décimaux ? Que prend-on pour les non-décimaux?
Si on permute les non décimaux en s'approchant des décimaux, on ne sera sans doute pas continu aux points non décimaux.
Je ne suis même pas convaincu qu'on puisse trouver une fonction continue sur un ensemble dense dans une autre et non continue sur son complémentaire, lui aussi dense...
#19 - 05-09-2011 12:44:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
une fonction à moitué continue partout
Il y a un exemple très connu de fonction réelle à valeurs réelles continue sur R−Q∗ et discontinue sur Q∗ mais je ne sais pas si on peu l'adapter aux décimaux et en plus l'application n'est pas bijective !!!
Vasimolo
#20 - 05-09-2011 13:53:05
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
une fonctiob à moitié continue partout
Je me suis mal exprimé 
Je pensais aussi à la bijection. Mais cette question me travaille. La continuité est trompeuse.
Si on prend:
f(x)=x pour x irrationnel
f(x)=0 pour x rationnel, on a bien une telle fonction.
Du coup, si on prend par exemple:
f(x)=x si x N'est PAS décimal
f(x)=-x si x est décimal
Qu'obtient-on?
C'est une bijection. Mais peut-on dire qu'elle est continue?
Elle n'est pas continue sur R.
Mais elle est continue sur D et sur R-D lorsqu'on restreint l'ensemble de définition à l'un ou a l'autre dans la mesure ou dans ce cas on exclut les points de discontinuité. Mais là on joue sur les mots.
Dans la question originale, il me semble que c'est la continuité à gauche sur R qui est demandée. Sinon il n'y a aucune question à vrai dire...
#21 - 05-09-2011 14:06:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
une fonction à moitié continie partout
rivas a écrit:Si on prend:
f(x)=x pour x irrationnel
f(x)=0 pour x rationnel, on a bien une telle fonction.
Une telle fonction ne me semble continue qu'en 0 
Vasimolo
#22 - 05-09-2011 14:42:02
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Une fonction moitié continue partout
f/Q est continue.
f/R−Q est continue.
Mais f/R n'est pas continue.
C'était ça mon point 
#23 - 05-09-2011 17:48:29
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Une fonctoin à moitié continue partout
J'aurais voulu répondre plus tôt mais mon pare-feu s'est amusé à bloquer mon accès à prise2tete 
La première fonction (proposition 1) est décrite plus en détail dans ma nouvelle énigme. Pour une description formelle :
Définition :
Si on écrit x=∑+∞j=−∞xj10j
alors f(x)=∑+∞i=−∞x2i+1102i+x2i102i+1
Voilà pour la définition rigoureuse. Je n'irais pas plus loin pour cette fonction, je ne veut ne pas spoiler ma nouvelle énigme.
Je vais étudier la fonction de la proposition 3 :
Appelons g cette fonction,
Définition :
Si x=∑bj=axj10j où xa≠0etxb≠0
Alors
1) si a=−∞ (nombre non décimal) g(x)=x
2) sinon si xa≠xa−1 alors g(x)=x+xa10a−1
3) sinon xa=xa−1 alors g(x)=x−xa10a
g n'est pas bijective je me suis trompé  (mais f est bien bijective) (mais f est bien bijective)
En effet g(1)=g(1,11)=1,1
Bon, comme c'est sur la continuité que cette fonction est intéressante, concentrons nous dessus :
1) Soit xun nombre décimal :
x=b∑j=axj10j
Considérons la suite ui=x−10a+∑a−1j=a−i9∗10j
Ecrit en écriture décimal ui=xbxb−1...xa+2xa+1(xa−1)99...999 (avec i fois le chiffre 9 à la fin)
g(u_i)=u_{i-1}[/latex] car g enlève le dernier chiffre quand il se répète. Or [latex]lim\ u_i = x[/latex] donc [latex]lim\ g(u_i)= lim\ u_{i-1} = x
mais g(x) \neq x donc g n'est pas continue en x
2) Soit xun nombre NON décimal :
lemme : Pour tout réel x', |g(x)-x|\ <\ 10^{n+2} si x_n \neq 0 (reprendre l'expression formelle de la fonction, majorer x_a par 10)
fin du lemme
Soit \epsilon >0
Soit maintenant m tel que \epsilon >10^m et tel que x_{m-3} \neq 0 <- c'est là que ça diffère des décimaux
alors quel que soit x' \in ]x-10^{m-3},\ x+10^{m-3}[
on a |g(x')-x'|<10^{m-1} (lemme)
d'où |g(x')-x| \ < \ |g(x')-x'|+|x' - x| \ <\ 10^{m-1}+10^{m-3}\ <\ 10^m
or g(x) = x
finalement |g(x')-g(x)| \ < \ \epsilon
donc g est continue en x
Pffiu ! Voilà c'est fini.
Je préfère être vague quand même ça prend moins de temps 
SVP répondez moi si vous avez compris, j'aimerais avoir des retours.
#24 - 05-09-2011 23:16:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
une foncrion à moitié continue partout
Je n'ai pas trop regardé pour les propositions 2 et 3 mais pour la 1ère ça fonctionne à merveille et c'est assez bluffant .
Très joli problème 
La discontinuité change quand même de côté en passant par 0 ce qui fait qu'un décimal échappe à la règle 
Vasimolo
#25 - 06-09-2011 18:28:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
une fonction à moitié continue pzrtout
Un exemple encore plus simple de bijection f continue sur \mathbb{R}-\mathbb{D} et discontinue sur \mathbb{D} .
On écrit chaque nombre réel avec une infinité de chiffres après la virgule ( des 0 à la fin pour les décimaux ) et on considère la fonction f qui après la virgule change tous les 0 en 9 et tous les 9 en 0 .
Mais f n'est pas involutive ( f\circ f \neq Id ) .
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum