Enigme Vu à la télé. @ Prise2Tete

JulesV · #1

Rien de mieux que les télés-matins japonais pour un réveil en douceur.

Vous savez ce qu'il vous reste à faire.

PS: j'ai la réponse (une approximation) mais pas de démonstration, je compte sur vous.

La réponse est de la forme WX.YZ avec cinq chiffres après la virgule, bonne réflexion!

masab · #2

La réponse est 9.00394 cm approximativement !

SabanSuresh · #3

J'ai pas compris ce qu'il faut calculer et je comprend rien au japonais. Mais j'ai trouvé sur le net que la valeur recherchée est 9,00394. Je vais donc voir à quoi ça peut correspondre.

JulesV · #4

masab:

Oui c'est ça bravo. Reste à le démontrer.

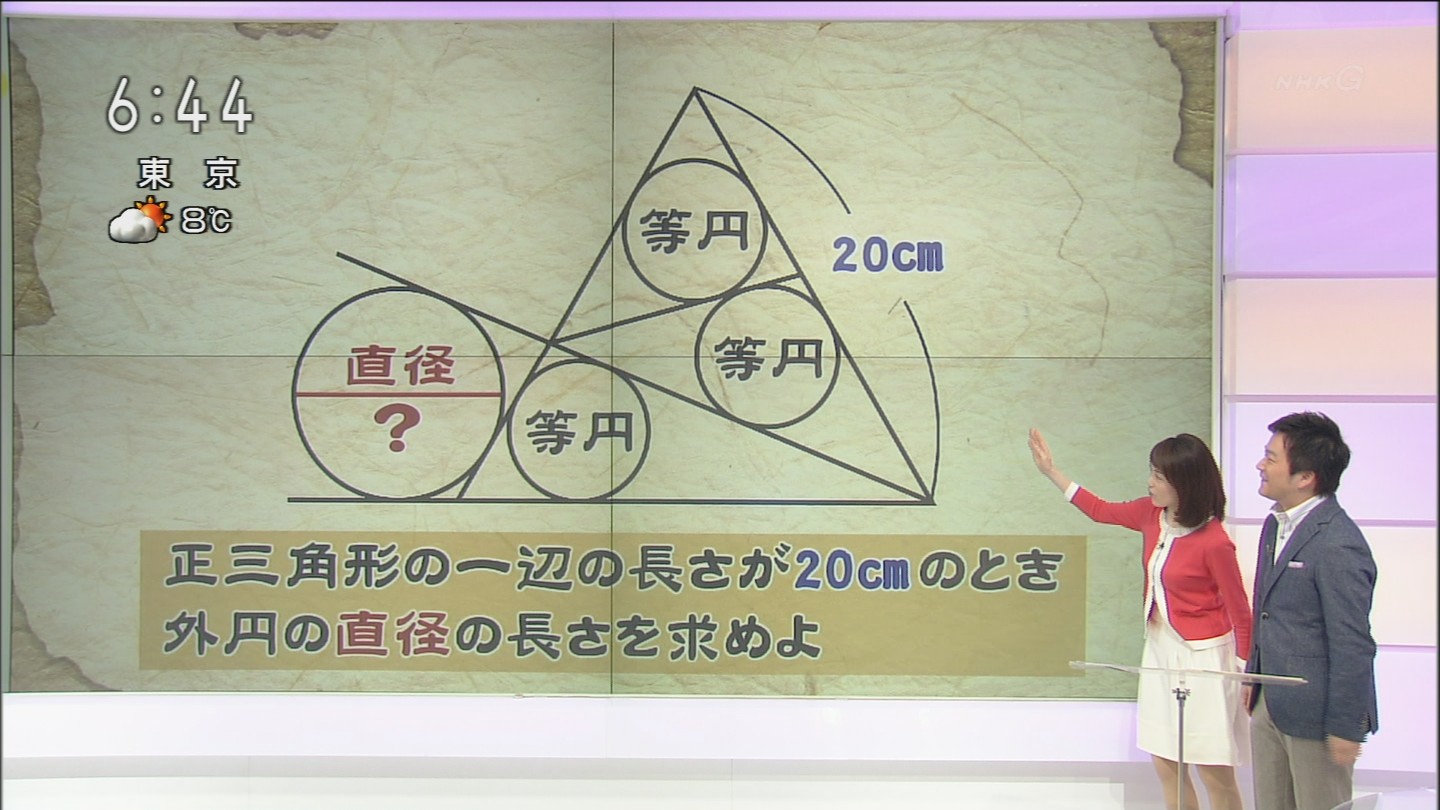
SabanSuresh: Tu as un triangle équilatéral de 20 cm, trois petits cercles de même rayon et tels que les tangentes se rencontrent sur le côté du triangle et tu dois rechercher le diamètre du grand cercle à gauche (avec le point d'interrogation).

golgot59 · #5

Comment sait-on que le grand triangle est équilatéral ? C'est dit dans l'énoncé ?

halloduda · #6

La réponse est de la forme WX.YZ avec cinq chiffres après la virgule

Il serait bon de savoir si c'est un point ou une virgule car il y a contradiction.

Sans démonstration, j'obtiens avec le logiciel graphique Geogebra,
en dépit du refus de la case réponse, un rayon égal à 4.50196... cm
Les chiffres suivants sont 46...

JulesV · #7

golgot59

Je suis partis de cette hypothèse et j'ai trouvé la réponse indiquée.

halloduda

Tu as trouvé la bonne réponse, il s'agissait en fait du diamètre comme indiqué sur la figure, désolé. Et j'utilise le point comme séparateur décimal.

Vasimolo · #8

Je trouve D=9,091389363 cm est refusé par la case réponse ai-je mal arrondi ?

Vasimolo

JulesV · #9

Vasimolo

Tu y es presque, ça cloche à partir de la deuxième décimale.

Vasimolo · #10

J'ai repris mes calculs , y'avait une petite erreur de signe . Le nouveau résultat D=9,003929287 n'est toujours pas validé par la case réponse

Vasimolo

Franky1103 · #11

golgot59 a écrit:
C'est dit dans l'énoncé ?

C'est clairement écrit en toutes lettres ... japonaises.

Vasimolo · #12

Je ne sais pas comment ont fait ceux qui ont obtenu le résultat , personnellement je n'ai pas trouvé de méthode purement géométrique . J'ai commencé par une chasse aux angles :

Puis en notant x=tan(a) et y= tan(b) , le triangle équilatéral et Wolfram donnent :

Après c'est facile , le rayon des petits cercles est $r=\frac{20}{x+\sqrt{3}}$ et celui du grand est $R=r.\frac{\sqrt{3}x+3}{\sqrt{3}x-1}$ .

Peut-on trouver ces longueurs sans passer par les valeurs approchées des angles ????

Dans les sangakus la solution n'est pas forcément élégante mais elle s'exprime toujours avec des radicaux ce qui n'est pas le cas ici .

Quelqu'un a une idée ?

Vasimolo

Franky1103 · #13

Je suis parti sur une autre piste, mais sans succès.
R=2.S/(a+b+c) avec 16.S²=(a+b+c).(-a+b+c).(a-b+c).(a+b-c)
donne 4.R²=(-a+b+c).(a-b+c).(a+b-c)/(a+b+c)
R étant le rayon du cercle inscrit et a, b, c les côtés du triangle.
Puis je voulais écrire l'égalité du rayon (ou des 4.R²) des 3 petits
cercles, mais les équations deviennent rapidement ingérables.

Vasimolo · #14

La valeur exacte du diamètre $D=20\sqrt{3}(\sqrt[3]{2}-1)$ .

Je suis sur le cul et j'attends la justification

Vasimolo

titoufred · #15

Le grand triangle est équilatéral ?

Nombrilist · #16

Oui.

Nombrilist · #17

Vasimolo a écrit:
La valeur exacte du diamètre $D=20\sqrt{3}(\sqrt[3]{2}-1)$ .

Je suis sur le cul et j'attends la justification

Vasimolo

Et dire que les japonais font ça de tête dès le matin au réveil.

SabanSuresh · #18

Je vais chipoter mais $D=20\sqrt{3}(\sqrt[3]{2}-1)$ vaut 9,0039292 qui doit être arrondi à 9,00393 et non à 9,00394.
Sinon pour la démo, je me permets de poser cette question : ne manque-t-il pas des données ?

halloduda · #19

Oui, SabanSuresh, tu as raison, regarde ma réponse initiale relative au rayon.

JulesV · #20

Merci à tous pour avoir participé à cette énigme.
Je suis également bluffé par la valeur trouvée (comment ?) par Vasimolo, à quoi peut donc correspondre une racine cubique ici...

SabanSuresh

Le problème n'est-il pas parfaitement parfaitement déterminé par ces données ?

SabanSuresh · #21

J'avais compris le problème mais je n'arrivais pas à démontrer ce 9,00394 : c'est pour ça que je n'ai pas posté.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 09-07-2013 15:52:21

Vu à la téléé.

#0 Pub

#2 - 10-07-2013 10:02:14

bu à la télé.

#3 - 10-07-2013 10:13:44

Vu la télé.

#4 - 10-07-2013 14:02:28

Vu à al télé.

#5 - 10-07-2013 15:10:12

Vu à la tél.

#6 - 10-07-2013 15:25:52

vi à la télé.

#7 - 10-07-2013 15:44:09

Vuu à la télé.

#8 - 11-07-2013 18:43:40

Vu à la tléé.

#9 - 11-07-2013 20:21:05

vu à la téké.

#10 - 12-07-2013 12:02:18

Vu à la tléé.

#11 - 12-07-2013 16:40:12

vu à la témé.

golgot59 a écrit:

#12 - 12-07-2013 19:01:49

Vu à la téé.

#13 - 12-07-2013 21:08:24

VVu à la télé.

#14 - 12-07-2013 23:27:43

Vu à la téél.

#15 - 13-07-2013 00:15:43

Vu à lla télé.

#16 - 13-07-2013 00:37:52

Vu à la téllé.

#17 - 13-07-2013 00:38:44

Vu à la télé

Vasimolo a écrit:

#18 - 13-07-2013 09:59:19

vu à la témé.

#19 - 13-07-2013 17:54:13

u à la télé.

#20 - 16-07-2013 19:00:21

vy à la télé.

#21 - 16-07-2013 20:26:54

Vuu à la télé.

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums