 |
#1 - 29-12-2014 13:13:39
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
lrs planètes
Dans un système, il existe 100 planètes sphériques de mêmes tailles, d'aire 1. Je décide de cultiver une plante sur ces planètes. Mais attention! On ne doit pas voir mes cultures d'une autre planète! Si on peut voir un point d'une planète depuis une autre, alors celui-ci n'est pas cultivable.

Quelle surface pourrai-je cultiver, exprimée en unité de surface de planète?
L'énigme n'est absolument pas de moi! Mais je la trouve intéressante. Je citerai sa source plus tard
PS: Image inutile, quoique
Un promath- actif dans un forum actif
#2 - 29-12-2014 15:47:08
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,002E+3
Les palnètes
Bah 1 est une réponse évidente si on imagine les planètes alignées.
#3 - 29-12-2014 16:32:12
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Les planètess
La réponse est évidente, mais la demonstration est plus importante
Un promath- actif dans un forum actif
#4 - 29-12-2014 17:24:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
les planèyes
Il est clair que si la réponse est unique elle ne peut être que 1 . Il suffit d'aligner les planètes sur une droite .
Après bien sûr il faut expliquer pourquoi la réponse est la même pour toute autre disposition .
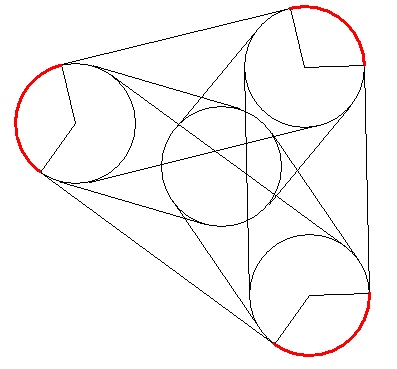
En fait ça à l'air assez évident par récurrence sur le nombre de planètes .
Vasimolo
#5 - 29-12-2014 17:24:44
- scrablor
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 965
lrs planètes
Les zones cultivées sont sur l'enveloppe convexe du système. Par des translations (99 au maximum), on peut reconstruire une planète identique, donc l'aire vaut 1.
Celui qui fuit les casse-tête ne vaut pas un clou.
#6 - 29-12-2014 17:28:54
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
leq planètes
C'est cela mais on attend une preuve
Un promath- actif dans un forum actif
#7 - 29-12-2014 18:03:06
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
les plznètes
Si on les aligne toutes, seules les 2 demi-sphères aux extrémités sont cultivables, donc 1.
J'ai fait la moitié du boulot : le cas aligné.
Je laisse les autres faire l'autre moitié, moi je suis fatigué.
#8 - 29-12-2014 18:11:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Le splanètes
D'après mon dessin qui n'est pas une preuve , on peut translater l'ensemble des parties invisibles sur une seule planète pour la recouvrir complètement sans superposition .
Il y a sûrement un moyen de montrer ça de façon plus évidente 
Vasimolo
#9 - 29-12-2014 18:39:20
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
les planètzs
Si j'aligne toutes les planètes, j'aurai: 2 x (1/2) = 1. Si je sors maintenant une planète de cet alignement en la plaçant n'importe où, je vois que la surface non vue de celle-ci augmente de la même valeur que les surfaces non vues des autres planètes diminuent. Je peux reproduire cette action autant de fois que je souhaite. La valeur 1 ne changera donc pas, quelle que soit finalement la position des 100 planètes.
#10 - 29-12-2014 19:14:42
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Les planète
golgot: pas mal c'est déjà ça 
Vasimolo: oui mais dans l'espace les planètes peuvent se répartir autrement. On attend une preuve rigoureuse 
FRanky: troisième ligne: preuve?
Un promath- actif dans un forum actif
#11 - 29-12-2014 19:37:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Les planètees
Il me semble qu'on peut supposer les planètes transparentes sans changer le problème et en le le rendant évident .
Vasimolo
#12 - 29-12-2014 19:47:55
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
lrs planètes
mais non ce n'est pas trivial du tout 
Un promath- actif dans un forum actif
#13 - 29-12-2014 19:54:38
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
les planèted
Je demande qq précisions: Dans un système, toutes les planétes tournent autour d'un soleil selon un plan. Les planètes ont une période de révolution, autour de leur soleil, variable selon les lois de Képler (masse et distance du soleil), mais heureusement toutes dans le même sens. De plus, elles tournent souvent sur elles mêmes, avec parfois un axe de pôle décalé du plan d'écliptique. Quid de ton système ?
#14 - 30-12-2014 10:33:42
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
kes planètes
salut.
je considère la sphère circonscrite aux 4 planètes telles que les 96 autres sont dans la sphère. sur ces 96 planètes , aucune n'est cultivable.
les planètes sont toutes de même taille . donc 4pi stéradians resteront invisibles des autres planètes. et cette ouverture angulaire correspond à la surface d'une planète . on peut donc cultiver sur une aire a = 1 je crois.
#15 - 30-12-2014 11:59:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
les planèteq
Bon je crois avoir l'idée 
On repère les points à la surface d'une planète en les identifiant par translation . Il est clair que si le pôle nord d'une planète n'est visible par aucune autre planète alors le centre de chacune des autres planètes se situera sous le plan de son équateur et sera donc visible par la planète . En bref un point de coordonnées données ne peut être invisible que sur une seule planète . Maintenant si on choisit un pôle , on peut trouver un plan passant par ce pôle en laissant toutes les planètes du même côté ( il y a quelques exceptions pour des points sur un nombre fini de cercles mais sans incidence pour l'aire ) : ce point n'est donc visible par personne .
Vasimolo
#16 - 30-12-2014 13:14:03
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
les planèyes
Le système est totalement indépendant, les planètes sont immobiles
Unecoudée: oui mais est-ce valable pour tout système?
Vasimolo:C'est ça! tu as bien prouvé l'unicité et l'existence! Chapeau 
Un promath- actif dans un forum actif
#17 - 30-12-2014 17:57:52
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Les planèes
salut.
pour un système ou les planètes sont alignées , dans ce cas on cultivera les 2
hémisphères extrêmes .
pour un système ou toutes les planètes sont sur un même plan , alors considère les planètes représentant les sommets d'un polygone convexe dont la somme des angles vaut toujours pi.(s-2) s étant le nombre de sommets . Les autres planètes sont à l'intérieur de ce polygone.
2pi pour un cercle correspond à 4pi stéradians pour une sphère . et dans ce cas on ne pourra cultiver que sur une unité d'aire à la surface de ces planètes extérieures.
#18 - 30-12-2014 19:55:23
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Le splanètes
S'ils ne sont pas sur un même plan?
Un promath- actif dans un forum actif
#19 - 30-12-2014 23:41:32
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Les planètees
Doit-on considérer que toutes les planètes ont leur centre sur une sphère imaginaire et tout le plus éloigné possible des autres ?
Doit-on considérer qu'elles sont sur un même plan? Qu'elles sont toutes alignées les unes derrière les autres...
J'avoue ne pas voir comment placer les planètes... 
Une fois cette question levée j'imagine qu'il faut faire des projections de cercle sur des sphères, un peu chiant mais pas très compliqués je pense. 
Shadock
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#20 - 31-12-2014 10:25:31
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
les pkanètes
Shadock: L'interêt est de montrer dans un cas général. Ne te complique pas avec des projections! 
Un promath- actif dans un forum actif
#21 - 01-01-2015 07:46:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Les plaètes
1 sphère !
Si on enveloppe le système d'une bâche, toutes les directions de l'espace issues du système sont entièrement données par les sphères, les plans de la bâche entre planètes n'apportant rien de plus qu'aux contours des sphères.
Attention cependant: tes légumes ne pousseront pas dans l'obscurité !
#22 - 01-01-2015 11:07:06
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Lees planètes
Si on suppose les planètes sur une même sphère et infiniment éloignées les une des autres, la moitié de la surface sera hors de vue pour chacune des planètes. Donc 50 !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#23 - 01-01-2015 12:16:08
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Les lanètes
Nodgim: c'est sur ce principe qu'il faut raisonner. Prouve l'existence et l'unicité de telles directions et ce sera bon.
Fix: non du coup, compte la planete à droite et à gauche d'elle. Ca enleve. Et les dirextions entre spheres restent les memes si le rayon augmente. De plus c'est un système fini, il est possible de me déplacer entre les planètes. S'agirait pas de mettre une infinité de temps à voir mes cultures 
Un promath- actif dans un forum actif
#24 - 01-01-2015 17:51:35
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Les planèes
L'unicité des directions et sens est évident pour un volume convexe, ce qui est bien le cas de l'enveloppe du système. C'est comme si on avait éclaté la surface d'une sphère en plusieurs morceaux. C'est un problème qui je crois a déja été posé sur ce site mais sous une autre forme, mais je ne sais plus laquelle.
#25 - 01-01-2015 17:55:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Les plantèes
A mon avis il faut du strictement convexe . L'enveloppe convexe de l'ensemble des planètes contient généralement des polygones plans et là il y a une infinité de points pour une direction donnée .
Vasimolo
Mots clés des moteurs de recherche
|
 |
|
Prise2Tete
Forum
Statistiques
Liste des membres
Hall of Fame
Contact
|

 Accueil
Accueil
 Forum
Forum








