@Franky1103 : j'ai trouvé une valeur inférieure à celle que tu annonces. As-tu une explication de ce résultat ?

@Sydre : en effet Je suis d'accord avec ton résultat, bravo ! Peux-tu m'expliquer ta démarche ?

De mon temps on appelait ça les kilos de cochons mais tout évolue

Je me suis amusé à faire une simulation sous "Scratch" ( un petit logiciel utiliser par les primaires et collégiens ) , en trente secondes on arrive à 36% .

Les calculs rigoureux risquent d'être un peu plus long

Vasimolo

Je n'ai rien vérifié et tout le monde sait que je fais beaucoup d'erreurs



Si tu ne connais pas le Scratch , ça risque de te paraître bizarre , personnellemnt ça me gonfle un peu ( euphémisme ) même s'il y a quelques bonnes idées .

Vasimolo

Bonsoir,
À défaut de trouver une méthode astucieuse, j'ai fait un script en python3 qui passe toutes les possibilités en revue.
Sauf erreur, je trouve une probabilité de faire "carotte" égale à 3/5.

Ebichu #12 a écrit:

@enigmatus : je pense qu'il y a erreur...

Effectivement, dans ma réponse en #11, pour une distribution donnée, je comptais autant de fois "carotte" que de joueurs pouvant le déclarer.

Voici ma nouvelle proposition : 169/385, soit environ 43,90%.

Salut !
Bon, je calcule juste les chances qu'un joueur ait 3 cartes identiques, les seules combinaisons possibles sont :
a,a,a,... : p1=3/11*2/10 = 3/55
a,a,b,a : p2=3/11*8/10*2/9 = 8/165
a,b,a,a : p3=8/11*3/10*2/9 = 8/165
a,b,b,b : p4=8/11*3/10*2/9 = 8/165
Donc la probabilité qu'un joueur ait un brelan est de p=p1+p2+p3+p4 = 0.2 tout pile

(Dans le cas où les trois joueurs auraient des jeux indépendants, on pourrait dire que les chances qu'au moins un joueur ait un brelan sont :
Le 1er : 0.2
Pas le premier mais le second : 0.8*0.2 = .16
Seulement le dernier : 0.8*0.8*0.2
D'où p = 0.2+0.16+0.128 = 0.488, C'est à dire presque une fois sur  2 !)

Malheureusement les cartes des joueurs sont interdépendantes... Je vais voir si je trouve un moyen simple de calculer ça

Bon, suite de la réflexion : Si le 1er joueur (p=.8) n'a pas de brelan, alors il y a 2 config possibles : Soit il a 2 paires, soit 1 paire et 2 singletons.
Les possibilités de 2 paires sont :
a-a-b-b : p1=3/11*8/10*3/9 = 4/55
a-b-a-b : p2=8/11*3/10*3/9 = 4/55
a-b-b-a : p3=8/11*3/10*3/9 = 4/55
Donc la probabilité que le premier joueur ait 2 paires est de p=12/55
Celle qu'il ait 1 seule paire et 2 singletons est de 0.8-12/55 = 32/55

Si le joueur 1 a 2 paires aabb (p=12/55), le seule moyen pour le joueur 2 d'avoir un brelan est d'obtenir la seule carte qui existe en 4 exemplaires. Les combinaisons sont : 3c et une autre carte ou 4c
p=4*2*4/8*3/7*2/6*2/5+4/8*3/7*2/6*1/5 = 17/70

Si le joueur 1 a 1 seule paire et 2 singletons aabc (p=32/55), pfff c'est plus compliqué...
Les combinaisons sont : bbb+a ou c, et idem avec ccc + a ou b
d'où p=2*4*2*3/8*2/7*1/6*3/5 = 12/70

Si je n'ai pas fait d'erreur (ce qui serait surprenant !), la probabilité que le 2ème joueur ait un brelan si le premier n'en a pas est de : p=0.8*(12/55*17/70+32/55*12/70) = 168/1375 (environ 0.12)

La suite à venir...

Je n'ai pas eu le courage de traiter tous les cas alors j'ai écrit un code en C# qui émule le problème :

var s = 0;

const int n = 1000000000;

var r = new Random();

for (var i = 0; i < n; i++)
{
    var h = new int[3, 3];

    double a = 4;
    double b = 4;

    for (var j = 12; j > 0; j--)
    {
         var c = r.NextDouble();

         if (c > (a + b) / j)
             h[j % 3, 0]++;
         else if (c > a / j)
         {
              h[j % 3, 1]++;

              b--;
         }
         else
         {
              h[j % 3, 2]++;

              a--;
         }
    }

    foreach (var t in h)
        if (t > 2)
        {
             s++;

             break;
        }
}

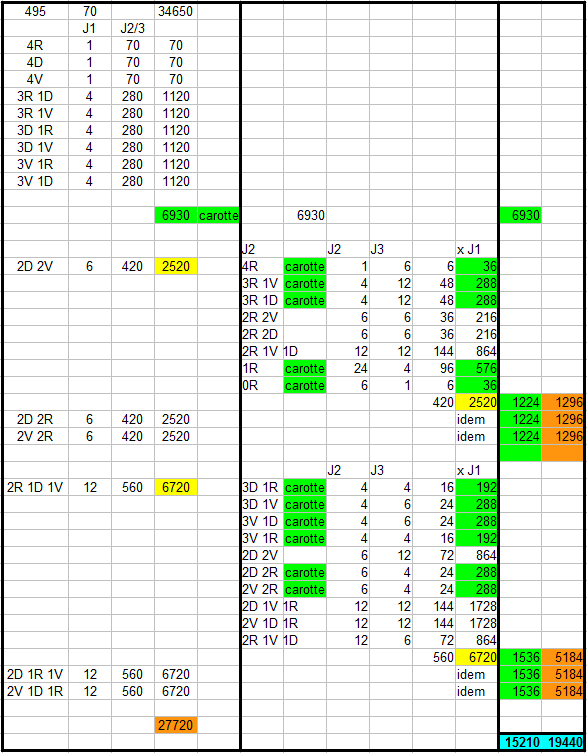
Juste en comptant... une genre de base 3.

12*11*10*9 positions /24 pour les rois, puis 8*7*6*5/24 pour les dames => 34650

Premier joueur :

une distribution (4-0-0) ou (3-1-0) et c'est gagnant : on se fiche des deux autres.

Second joueur : en tenant compte du fait que le premier a eu une distribution  (2-2-0) ou (2-1-1) idem.

Après, il faut juste un peu de rigueur en comptant, mais ça n'est pas bien long à faire.

Merci à tous les participants. Je vous livre une solution que j'ai essayé de rendre la plus succincte possible.

On note A, B, C les trois hauteurs possibles sans préciser si ces lettres signifient As, ou Roi, ou Dame.

Si l'on différencie les 12 cartes, le premier joueur peut avoir C(4;12)=495 mains différentes.

Le premier joueur peut avoir une main du type :
*AAAA (3/495)
*AAAB (96/495)
*AABB (108/495)
*AABC (288/495)

Je détaille le calcul pour cette dernière fraction, les autres fractions de cette solution s'obtiennent par des raisonnements similaires. On trouve 288 mains en faisant 3 * C(2;4) * 4 * 4 : 3 est le choix de la hauteur correspondant à A (A=As ou A=Roi ou A=Dame), C(2;4) est le nombre de paires de A possibles (pique+coeur ou pique+carreau ou ...), 4 est le choix de la couleur de B (pique ou coeur ou ...) et 4 est le choix de la couleur de C.

Dans les deux premiers cas, le premier joueur a (au moins) un brelan et l'affaire est entendue. Dans les deux derniers cas, il faut aller voir si le deuxième ou le troisième joueur n'auraient pas un brelan. Il reste alors C(4;8)=70 mains possibles pour le deuxième joueur, la main du deuxième joueur déterminant alors celle du troisième.

Dans le cas AABB, les deux autres joueurs peuvent avoir des mains du type CCCC + AABB (2/70), ou CCCx + xxxx (32/70), ou pas de brelan (34/70).

Dans le cas AABC, les deux autres joueurs peuvent avoir des mains du type BBBA+CCCA (4/70), ou BBBC+CCAA (6/70), ou CCCB+BBAA (6/70), ou pas de brelan (54/70).

La probabilité qu'il y ait carotte est donc 3/495 + 96/495 + 108/495 * 34/70 + 288/495 * 16/70 = 169/385.

Bravo à ceux qui avaient ce résultat !

Mais on veut se prendre la tête ! Sinon on ne pourrait pas en faire un problème pour ce site

Sinon, je pense que tu as oublié le cas où les joueurs obtiennent AARR, AADD et RRDD.