En partant du principe qu'il s'agit des aiguilles pour les heures et les minutes (exit la trotteuse)

A chaque minute qui s'écoule, l'aiguille des minutes avance et réduit l'écart de 6° (360°/60) et celle des heures avance et augmente l'écart de 0,5° (30°/60).

Les minutes écoulés sont alors:
Soit [latex]156-6x+0,5x=10 \Rightarrow x=\dfrac{146}{5,5}\approx 26 min\; 33 s[/latex]

Soit [latex](360-156)-6x+0,5x=10 \Rightarrow x=\dfrac{194}{5,5}\approx 35 min\; 16 s[/latex]

EDIT: On la refait; moins crispé.
Il y a deux possibilités pour commencer:
Soit l'angle orienté (dans le sens trigonométrique) des heures vers les minutes vaut 138° et on aura:
[TeX]138-5,5x=\pm 60[/latex] selon que l'aiguille des minutes dépasse ou non celle des heures

Soit c'est l'angle orienté des minutes vers les heures qui vaut 138° et on aura:
[latex]138+5,5x=360\pm 60[/TeX]
De ces quatres possibilités, une seule donne un compte de minutes exactes qui vaut: 36 min

En une heure, la grande aiguille parcours 360°, soit 6° par minute
La petite en parcours 360/12 = 30, soit 0,5° par minute

La grande gagne donc 5,5° par minute sur la petite

4 cas possibles :



[...]

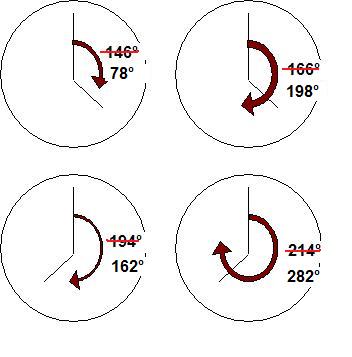
OK 138° puis 60° ...

Donc 78°, 198°, 162° ou 282°;

Seuls 198° sont divisibles par 5,5, nous sommes donc dans le cas en haut à droite et il s'est écoulé 36mn pendant lesquelles la grande aiguille a dépassé la petite.

De plus la seule heure qui permette de trouver ce résultat de minute pile en minute pile me semble être 2h 36 , puis 3 h 12

Pourquoi as-tu changé les valeurs de l'énoncé alors qu'elles donnaient un solution ?

Bref avec les nouvelles valeurs, la réponse est :
36 minutes entres 9h24 (resp. 21h24) et 10h00 (resp. 22h00)

EDIT
Petite démo dans le cas général.
Je note l'heure 1 [latex]h_1:m_1[/latex] et l'heure 2 [latex]h_2:m_2[/latex]
La grande aiguille fait un angle en degrés avec la verticale égal à :
[TeX]30h_1+\frac{m_1}2[/latex] et [latex]30h_2+\frac{m_2}2[/TeX]
La petite aiguille fait un angle en degrés avec la verticale égal à :
[TeX]6m_1[/latex] et [latex]6m_2[/TeX]
La différence entre ces 2 angles vaut en valeur absolue donc :
[TeX]|30h_1-\frac{11m_1}2|[/latex] et [latex]|30h_1-\frac{11m_2}2|[/TeX]
Mais cette différence peut dépasser 180°, donc si on veut que l'angle formé par les aiguilles soit égal à un angle [latex]\alpha[/latex] il faut considérer 2 cas : la différence vaut [latex]\alpha[/latex] ou [latex]360-\alpha[/latex]

Dans le cas qui nous intéresse, [latex]\alpha_1=138[/latex] et [latex]\alpha_2=60[/latex]

Pour la première heure, il faut donc chercher les solutions vérifiant :
[TeX]30h_1-\frac{11m_1}2=138[/TeX]
ou [latex]30h_1-\frac{11m_1}2=-138[/latex]
ou [latex]30h_1-\frac{11m_1}2=222[/latex]
ou [latex]30h_1-\frac{11m_1}2=-222[/latex]
que l'on peut écrire (avec [latex]k_1=\frac{m_1}6[/latex] entier car 138, 222 et 30 sont divisible par 6, et 11 premier avec 6, donc [latex]m_1[/latex] divisible par 6)
[TeX]10h_1=11k_1+46[/TeX]
ou [latex]10h_1=11k_1-46[/latex]
ou [latex]10h_1=11k_1+74[/latex]
ou [latex]10h_1=11k_1-74[/latex]

ce qui donne les solutions :
[TeX]k_1=4[/latex] et [latex]h_1=9[/latex] : 09h24 ou 21h24
[latex]k_1=6[/latex] et [latex]h_1=2[/latex] : 02h36 ou 14h36
[latex]k_1=6[/latex] et [latex]h_1=14[/latex] : impossible
[latex]k_1=4[/latex] et [latex]h_1=-3[/latex] : impossible

On arrive à quatre heures possibles pour la première heure : 02h36 ; 09h24 ; 14h36 ; 21h24

Pour la seconde heure, c'est le même raisonnement :

[latex]30h_2-\frac{11m_1}2=60[/TeX]
ou [latex]30h_2-\frac{11m_2}2=-60[/latex]
ou [latex]30h_2-\frac{11m_2}2=300[/latex]
ou [latex]30h_2-\frac{11m_2}2=-300[/latex]
que l'on peut écrire (avec [latex]k_2=\frac{m_2}{30}[/latex] entier car 60, 300 et 30 sont divisible par 30, et 11 premier avec 6, donc [latex]m_2[/latex] divisible par 30 ; [latex]k_2[/latex] vaut 0 ou 1)
[TeX]2h_2=11k_2+4[/TeX]
ou [latex]2h_2=11k_2-4[/latex]
ou [latex]2h_2=11k_2+20[/latex]
ou [latex]2h_2=11k_2-20[/latex]

ce qui donne les solutions :
[latex]k_2=0[/latex] et [latex]h_2=2[/latex] : 02h00 ou 14h00
impossible
[latex]k_2=0[/latex] et [latex]h_2=10[/latex] : 10h00 ou 22h00
impossible

On arrive à quatre heures possibles pour la seconde heure : 02h00 ; 10h00 ; 14h00 ; 22h00.

Les seuls configurations où il s'est écoulé moins d'une heure entre les 2 moments sont :
09h24 puis 10h00
21h24 puis 22h00

Il s'est donc écoulé 36 minutes.


Tu avais dans un premier lieu donné les valeurs 156° et 10°, on arrivait aux heures : 02h48 et 4h20, avec une différence de 1h32. Tu n'avais pas encore spécifié que moins d'une heure s'était écoulée, donc il y avait bien une solution, tant pis

Je me suis un peu planté dans mes vitesses angulaires. =D

La vitesse angulaire de l'aiguille des heures vaut 30°/h.
Celle de l'aiguille des minutes vaut 360°/h. Comme les 2 aiguilles tournent dans le même sens, la vitesse angulaire relative vaut 330°/h.
Si l'angle diminue de 138°-60°=78°. 78° / 330°/h = 0,236364 h = 00h14,182.
Si l'angle augmente de 360°-138°-60°=162°, 162° / 330°/h = 0,490491 = 00h29,455.

Je n'obtiens pas de minute exact.

Edit: il n'est pas impossible que les 2 aiguilles se soient croisées.

J'ai 2 cas:

- l'angle parcouru vaut 138°+60°=198° et on trouve 198° / 330°/h = 0,6 = 00h36.

- l'angle parcouru 360°-138°+60°=282° et on trouve 282° / 330°/h = 0,854545 = 00h51,273.

Ceux n'ayant participé qu'a une question, je leur conseille fortement de participer aux autres.

138 - 60 = 78 dg
La grande aiguille court après la petite.
La petite aiguille allant 12 fois moins vite que la grande, celle-ci a parcouru :
78 * 12 / 13 = 90 dg, ce qui représente 15 mn.

Bonjour,
La petite aiguille avance 12 fois moins vite que la grande. De plus on connait l'angle avant (138° équivalent à 23mn) et après (60° équivalent à 10mn), mais on ne sait pas si c'est la grande aiguille qui est devant la petite ou l'inverse: on aura donc 4 cas à considérer (k étant un entier) exprimant l'angle en fonction du temps passé t:
1°) 11/12 t + 23 = 60 k + 10 soit t = 12/11 (60 k - 13)
2°) 11/12 t + 23 = 60 k - 10 soit t = 12/11 (60 k - 33)
3°) 11/12 t - 23 = 60 k + 10 soit t = 12/11 (60 k + 33)
4°) 11/12 t - 23 = 60 k - 10 soit t = 12/11 (60 k + 13)
Je fais varier k et je garde les valeurs entières de t comprises entre 0 et 60.
La seule valeur qui convienne est le cas 3° avec k = 0 et qui donne t = 36.
La grande aiguille a parcouru un angle équivalent à 36mn (soit 216°) (en dépassant la petite) et la petite un angle équivalent à 3mn (soit 18°). L'angle initial de 138° est devenu 216 - 18 - 138 = 60° (ou en équivalent minutes 36 - 3 - 23 = 10).
Donc la réponse unique est 36mn.
Bonne journée.
Frank

13 minutes

Si moins d'une heure s'est écoulée entre les deux instants, alors la seule possibilité est que Griego a regardé pour la première fois son horloge à 9h24 (ou 21h24), puis la seconde fois à 10h00 (ou 22h00).

Aussi, dans les deux cas, le nombre de minutes écoulées entre ces deux instants est de 36 minutes.

Sympa comme petit problème