 |
#26 - 14-12-2017 19:56:20
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,066E+3
des nombred premiers inégalement répartis ?
C'est chouette de savoir compter... Ordinateur à l'appui.
Mais au bout du compte, vous discutez d'une conjecture raisonnable (et largement traitée) , sans apporter grande eau au moulin.
#27 - 14-12-2017 22:38:57
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Des nombre premiers inégalement répartis ?
@scarta : merci pour ton code et pour ces graphes. Effectivement, ça devient difficile de contester qu'il y a une déviation. Je ne crois plus à une éventuelle inversion.
@gwen27 : "largement traitée" ? Je n'ai pas trouvé de source sur le web concernant cette conjecture, mais j'ai une connexion de piètre qualité ce qui ne facilite pas mes recherches. Peux-tu me donner un lien, ou le nom de cette conjecture ?
#28 - 14-12-2017 23:02:26
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,066E+3
des nombres premiers inégzlement répartis ?
Bah cherche "premiers 6k+-1"
#29 - 15-12-2017 08:41:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3827
des nombres premiers inégalemrnt répartis ?
Pffff.....
C'est très destructeur pour la créativité, ces références qu'on peut trouver sur le net. Aujourd'hui, n'importe quelle suite qu'on pense un tant soit peu originale est déja présente quelque part. Avant de trouver si un truc qui semble original n'existe pas déja, il faut passer son temps à faire une recherche sur le net.
C'est décourageant.
Pour ce thème abordé ici, je l'ai lu dans un vague article mathématique qui ne donnait pas de précision, ça m'a intérressé, j'y ai regardé de plus près. Cela dit, je n'ai rien trouvé de probant, seulement un début de piste, un semblant d'explications, et ai tenté de faire partager cette curiosité.
Il serait extrêmement présomptueux de croire que les amateurs que nous sommes peuvent apporter la moindre contribution aux mathématiques, surtout pour les thèmes très étudiés comme les nombres premiers ! Il y a suffisamment de gens bien plus compétents que nous qui s'en occupent.
#30 - 15-12-2017 09:35:03
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1972
Des nombres premiers ingalement répartis ?
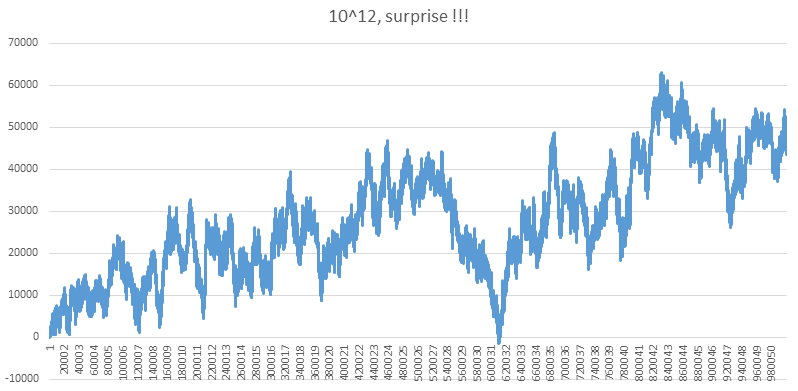
Et attention, surprise du jour !!!!
#31 - 15-12-2017 09:41:12
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1972
Des nombres preemiers inégalement répartis ?
nodgim a écrit:Il serait extrêmement présomptueux de croire que les amateurs que nous sommes peuvent apporter la moindre contribution aux mathématiques, surtout pour les thèmes très étudiés comme les nombres premiers ! Il y a suffisamment de gens bien plus compétents qui nous qui s'en occupent.
Sans être présomptueux, je pense qu'on se défend 
Sauf erreur dans mon code (pas impossible), tu as maintenant la preuve de l'inversion
Première inversion entre 609045M et 609058M
Ensuite entre 609129M et 609154M
Ensuite entre 609176M et 609246M
Et quelques autres ensuite
#32 - 15-12-2017 15:50:54
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3827
Des nombres premiers inégalment répartis ?
Bravo Scarta, ta persévérance a payé !
Combien de temps de calcul ?
Il y a peut être quelque part, sûrement même, des matheux qui étudient ça de près, avec sans doute des moyens plus étendus, et des approches théoriques poussées, qui n'ont rien à voir avec ce qu'on fait ici.
C'est épatant comme jusqu'à 10 ^ 10 on pensait l'inversion possible, avec 10^11 non, et la preuve de l'inversion est venue avec 10^12.
Comme quoi, aucune projection ne doit être faite sur une base heuristique.
- Il y a peut être un nombre fini de nombres premiers jumeaux.
- Il y a peut être une boucle autre que 1,4,2 dans l'algorithme de Syracuse.
- Il y a peut être une exception à la conjecture de Riemann.
-.......
#33 - 15-12-2017 16:33:57
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1972
des nombrrs premiers inégalement répartis ?
Environ 6h pour trouver l'inversion et 10 pour la totale
#34 - 15-12-2017 17:58:56
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,066E+3
des nombres premiers inégamement répartis ?
N'importe qui (enfin, peut-être pas n'importe qui quand même) peut avoir l'idée d'une méthode simple qui aurait échappé à des yeux avertis. Mais c'est vrai que 2 clics permettent de trouver la plupart des sujets déjà traitée, tout ou en partie.
#35 - 15-12-2017 19:27:17
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Des nombres premiers inégalemen répartis ?
Bravo scarta pour ce joli résultat ! C'est tout de même troublant de voir comme l'inversion est minime et dure peu de temps, avant que la courbe reparte crever le plafond. Il y a peut-être une raison derrière, mais bon courage pour la trouver...
Il est vrai que beaucoup d'idées ont déjà été eues puis documentées sur le web, mais quand on prend un sujet spécifique et qu'on le creuse bien (ça prend souvent quelques jours), on finit quand même par en faire le tour et par imaginer de nouvelles choses. Sinon les chercheurs seraient au chômage... Plus le temps passe et plus le nombre de questions ouvertes augmente, et il n'est pas nécessaire d'être une pointure pour être original. Pour démontrer la conjecture de Riemann, oui, mais il y a plein de résultats plus simples qui attendent.
@gwen27 : google ne m'a rien renvoyé de pertinent, mais au risque de me répéter, je ne peux pas consulter plus de quelques pages... As-tu un lien précis à me soumettre ?
#36 - 15-12-2017 23:22:20
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,066E+3
Des nombres premier inégalement répartis ?
Pas plus que ça... Sûrement pas plus que ceux que tu as trouvés. Juste le fait que le sujet a été creusé et reste non déterminé ce qui est déjà pas mal révélateur.
Une telle affirmation serait quand même assez remarquable pour être (de manière vérifiable facilement) plus qu'une conjecture
#37 - 16-12-2017 09:00:44
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3827
DDes nombres premiers inégalement répartis ?
Je ne sais pas trop de quelle affirmation tu parles Gwen...
Perso, je conjecture, identiquement aux 6k+/-1, et pour la même raison, que les nombres premiers 4k+1 sont globalement moins nombreux que les nombres premiers 4k-1.
#38 - 16-12-2017 10:42:55
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Dse nombres premiers inégalement répartis ?
Pour ma part, je prévois que les nombres premiers de la forme 2k+1 sont rigoureusement aussi nombreux que ceux de la forme 2k-1. 
#39 - 16-12-2017 22:56:32
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1972
des nombres premiers inégalement répattis ?
Et moi que le ratio "premiers pairs"/"premiers impairs" tend vers 0.
#40 - 17-12-2017 10:28:46
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
des nombrzs premiers inégalement répartis ?
J'ai adapté le code de scarta en c++ et je l'ai refait tourner sur mon antique processeur. Le premier nombre premier pour lequel il y a une inversion est 608981813017.
Un petit coup de google et on trouve deux suites de oeis, dont l'une contient des liens vers des articles parlant de ce problème.
#41 - 17-12-2017 12:15:45
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Des nombres premiers inégalement répartis ??
http://www.dms.umontreal.ca/~andrew/PDF/PrimeRace.pdf
Où l'on apprend que ce nombre a été calculé pour la première fois à Noël 1976, on n'a que 41 ans de retard 
Généralement c'est plutôt le nombre juste après, 608981813029, qui est cité, car ils font la course entre les 3k+1 et les 3k+2, donc 2 rentre en ligne de compte ce qui décale le total d'une unité.
#42 - 17-12-2017 14:07:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3827
Des nombrs premiers inégalement répartis ?
pfff...Je passais mon bac à cette époque....
#43 - 17-12-2017 14:29:58
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3234
- Lieu: Luxembourg
des nombres premiers inégalemeny répartis ?
Le bac en 1976 ? Je te croyais bien plus jeune.
#44 - 17-12-2017 16:18:06
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1972
Des nombres premiers inégalement répatris ?
Mon père passait son bac à cette époque...
Ah non c'était en 77
#45 - 17-12-2017 16:48:04
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3234
- Lieu: Luxembourg
ses nombres premiers inégalement répartis ?
Ah, donc c'est moi le vieux.
J'ai passé mon bac en 1980.
|
 |

 Accueil
Accueil
 Forum
Forum







