Salut arobase,

Ci-dessous la solution du problème, façon devoir de physique au lycée.

Choix du référentiel

On considere les boules comme des solides ponctuels.
On sait que les boules vont rester dans le plan du support. Cela veut dire que les forces restent dans le plan.

On sait que les composantes des forces perpendiculaires au plan incliné (axe z)  s'annulent, sinon on verrait les boules sauter hors du plan.

On peut donc ne pas tenir compte de l'axe z pour les calculs.



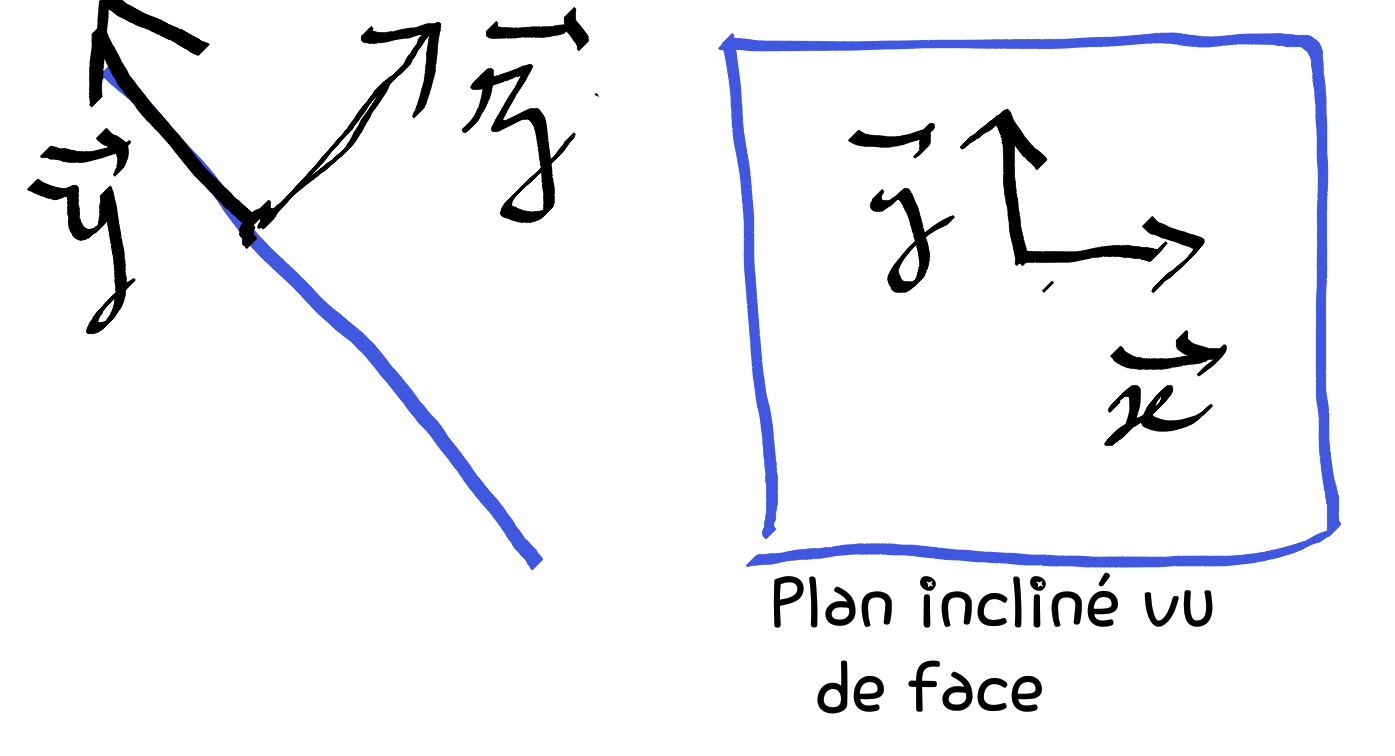
On choisit donc comme repère le plan du support (x horizontal vers la droite, y vers le "bas" tout en restant dans le plan du support) et z perpendiculaire au support.

Forces en présence

La gravité avec une composante dans le plan du support une composante perpendiculaire au support qui va être exactement annulée par la force de réaction du support.


La réaction du support avec :
- une composante perpendiculaire au support (luttant exactement contre la gravité)

- Les frottements contenus dans le plan du support : a vitesse pas trop grande, ils devraient être linéaires, opposés à la vitesse.

Désolé je ne suis pas un expert en mécanique et en frottements, cela mériterait d'approfondir. Je pense néanmoins qu'à des vitesses raisonnables on peut schématiser comme j'ai dit.

PS : Pour la résistance de l'air, je sais que les frottements sont linéaires aux petites vitesses. Puis le frottement devient quadratique (en [latex]v^2[/latex]) à des vitesses importantes.

Valeur des forces

Frottements :   [latex]      \overrightarrow{F_f} = -f.\overrightarrow{v}[/latex]

Gravité :
Soit [latex]\alpha[/latex] l'angle du plan avec la verticale .
[TeX]\overrightarrow{F_g} = m .\overrightarrow{g}[/TeX]
(NB : [latex]\overrightarrow{g}[/latex] est le vecteur de la gravité du lieu, qui est dirigé vers le bas et vaut [latex]9,81 m.s^{-2}[/latex])

La composante de la gravité dans le plan du support est
[TeX]-g.cos(\alpha) \overrightarrow{y}[/TeX]
Rem : la composante perpendiculaire est
[TeX]-g.sin(\alpha).\overrightarrow{z}[/TeX]
mais comme on a dit, elle ne sert pas dans les calculs.

somme des forces et accélération de la boule

On obtient l'accéleration grâce à la 2e loi de Newton :
[TeX]\sum{ \overrightarrow{F}} = m\overrightarrow{a}[/TeX]
Soit ici :
[TeX]m\overrightarrow{a} = -mg.cos(\alpha) .\overrightarrow{y} -f.\overrightarrow{v}[/TeX]
On divise par m à gauche et à droite et on definit un coeff c=f/m pour que ce soit plus court à écrire.
[TeX]\overrightarrow{a} = -g.cos(\alpha) .\overrightarrow{y} -c.\overrightarrow{v}[/TeX]
Nous avons des accélerations et des vitesses dans la même équation, et comme on le sait l'acceleration est la derivée de la vitesse. Ca va donc donner des equations differentielles.

Precisions sur les notations
[TeX]\overrightarrow{a} = d\overrightarrow{v}/dt[/TeX]
C'est-à-dire
[TeX]a_x = dv_x/dt[/TeX]
[TeX]a_y = dv_y/dt[/TeX]
Comme on ne fait que des dérivations par rapport au temps, on va utilsier la notation classique avec des '
[TeX]a_x = v_x' [/TeX]
[TeX]a_y = v_y' [/TeX]
Revenons à nos moutons, nous en étions à :
[TeX]\overrightarrow{a} = -g.cos(\alpha) .\overrightarrow{y} -c.\overrightarrow{v}[/TeX]
Cela donne sur l'axe des x :
[TeX]v_x' = -c v_x[/TeX]
Et sur l'axe des y :
[TeX]v_y' = -c v_y - g.cos(\alpha)[/TeX]
Ce sont donc deux équations différentielles (à resoudre séparément)

On ne panique pas et on sort son cours sur les "equadiffs".

https://www.maths-cours.fr/supplement/e … rentielles

Bon là, ce n'est plus assez frais pour moi, pour justifier proprement, mais ça doit donner cela :

Les solutions de y' +ay = 0 sont les
fonctions de la forme x -> k.exp(-ax) avec k un entier quelconque.

Sur l'axe x :
[TeX]v_x' + c.v_x = 0[/TeX]
=> les solutions possibles sont
[TeX]v_x(t) = k_1.exp(-c.t)[/TeX]
avec  [latex]k_1[/latex] un entier quelconque.

Sur l'axe y :
[TeX]v_y' + c.v_y + g.cos(\alpha) = 0
=> v_y(t) = k_2.exp(-c.t) - g.cos(\alpha)/c
[/TeX]
Avec [latex]k_2[/latex] un entier quelconque.

Verif : [latex]v_y' = -c.k_2.exp(-c.t)[/latex]
d'où [latex]v_y' + c.v_y =  -c.k_2.exp(-c.t) + c.(k_2.exp(-c.t) - g.cos(\alpha)/c ) = -g.cos(\alpha)[/latex]

On peut determiner [latex]k_1[/latex] et [latex]k_2[/latex] si l'on connait la vitesse à un temps t donné. Par exemple, la vitesse de départ au temps t=0
[TeX]v_0 = (v_{x0}, v_{y0})[/TeX][TeX]v_x(0) = k_1.exp(0) = k_1[/TeX]
donc [latex]k_1=v_{x0}[/latex]

Et [latex]v_y(0) = k_2.exp(0) - g/f[/latex]
donc [latex]k_2 - g/f = v_{y0}[/latex]
donc [latex] k_2 = v_{y0}+g/f[/latex]

Mais je garde [latex]k_1[/latex] et [latex]k_2[/latex] par la suite car c'est plus concis.

Position de la boule en fonction du temps

On intègre ces fonctions vitesse pour obtenir la position en fonction du temps
[TeX]x(t) = \int_{0}^{t}  k_1.exp(-f.t) \, \mathrm{d}t
=-( k_1/f ).exp(-f.t) + m_1[/TeX][TeX]y(t) = \int_0^t k_2.exp(-c.t) - g.cos(\alpha)/c  \, dt = (-k_2/c)exp(-ct)-g.cos(\alpha).t/c + m2[/TeX]
Avec m1 et m2 deux constantes qui peuvent etre determinées si on connait la position de la boule, par exemple sa position au départ, à t=0.

Reflexion

En me lançant dans le calcul, je pensais trouver une formule avec une sorte d'hyperbole (dégradée par les frottements) avec une boule qui file tjs plus vite vers le bas... Autrement dit, une position en y=-at^2+...

Mais il n'en est rien. La vitesse converge vers une constante.

A la reflexion, c'est tout simplement normal. La vitesse est limitée aux grandes vitesse, car les frottements deviennent supérieurs à la gravité.

Par conséquent, il y a une vitesse d'equilibre ou la gravité compense exactement les frottements [latex]g.cos(\alpha)=c.v_{ymax} => v_{ymax} = g.cos(alpha)/c[/latex]

Et on ne peut pas depasser cette vitesse.