Salut Caduk !

Aïe, je n'ai pas le même résultat, mais comme je ne suis pas sûr de ma réponse...

En fait la question m'a été posée par mon frère, et cette question lui est venue comme ça, sans le vouloir. Du coup, je ne sais même pas si il y a une littérature là dessus.

Bref, ce sera intéressant de comparer nos réponses pour les comparer et trouver la bonne. Il faudrait que je refasse mes calculs mais perso j'avais trouvé :
Spoiler : [Afficher le message] 1/3

Il va falloir que je me rappelle mon cheminement...

Salut Franky !

Bon, tu trouves comme Caduk... Je crois que je vais pleurer, je n'avais pas ça, snif...

J'attend la fin de la période pour en discuter

Salut Jackv !

Bon, je viens de refaire les calculs et maintenant je trouve comme vous. Je ne sais pas où je m'étais trompé. Désolé pour l'insinuation d'erreur que j'avais laissé entendre au départ.

Bravo à vous 3 !

J'espère que ça vous aura au moins un peu amusé.

Salut,

Sauf erreur [latex](1-\frac{2}{\pi})D\approx 0,3633D[/latex] avec [latex]D[/latex] la distance entre l'astronaute et l'objet.

Dans un plan, ce serait Pi / 4 fois la distance donnée . Ce pourrait être la même chose dans l'espace, mais je n'en suis pas sûr....

Coucou,

Disons que le point A essaie de se rapprocher du point B en suivant une droite (D) passant par A. Posons soit I la projection de B sur (D), I le point le plus proche de B. soit alpha l'angle (AB)^(D)

En partant du principe qu'on cherche le rapprochement moyen sous la forme (Distance Après / Distance Avant), ce rapprochement est l'espérence de la valeur IB (pub pour un site de vente aux enchères?)

On remarque aussi que par le jeu des symétries, l'espérence de rapprochement est la même dans les quatre quadrants (pour alpha de 0 à pi/2, de pi/2 à pi, etc.)

En supposant que la distance initiale vaut une unité, je calcule l'espérance de la distance finale en intégrant entre 0 et [latex]\frac{\pi}{2}[/latex]

Cela donne [latex] \frac{\int_{0}^{\frac{\pi}{2}} cos(\alpha) \, \mathrm{d}\alpha }{ \frac{\pi}{2}}[/latex]

=  [latex]\frac{[ sin(\alpha) ]_0^\frac{\pi}{2} }{ \frac{\pi}{2} }[/latex]

=  [latex]\frac{[ 1 - 0 ] }{ \frac{\pi}{2} } = \frac{2}{\pi} [/latex]


En conclusion, (Distance Après / Distance Avant) vaut en moyenne [latex]\frac{2}{\pi} [/latex]

de tête, deussurpi, non?

ça pourrait être 2/PI, calculé à partir de l'intégrale de sin x entre 0 et Pi/2.

Alors, pour le coup, ça me pose un drôle de problème avec ma 1ère réponse à Pi/4.

Dans ma 1ère réponse, pour un x donné dans [0,1] en supposant 1 la distance entre les 2 points, j'ai fait l'intégrale de V(1-x²). Je me justifiais l'usage de x au lieu d'un angle par le fait que pour un angle donné, il n'y avait qu'un seul x sur la droite qui est le plus proche du point visé ( donc bijection angle / x )

D'où, pour l'instant, ma très grande perplexité sur la double réponse. Et surtout, à quoi correspond donc la 1ère réponse que j'ai faite ?

Bonsoir,

Je pense que l'ambiguïté dans les réponses provient de l'interprétation de cette phrase : "Si une droite aléatoire de l'espace passe par votre position"

O : observateur
C : cible
M : intersection de la demi-droite issue de O avec la sphère de centre O et de rayon OC (tel que l'angle (OC,OM) soit aigu)
P : projection de M sur OC
y = OP

On peut supposer OC=1

Pour moi, les points M doivent être équirépartis sur la demi-sphère, ce qui entraîne que les points P sont équirépartis sur OC.

La moyenne des distances minimales est alors :
somme(de 0 à 1) sqrt(1-y**2) *dy

Avec le changement de variable : y = sin(a)
somme(de 0 à pi/2) (cos(a))**2 *da

J'obtiens, sauf erreur : pi/4

Salut enigmatus !

Bon, je vais poster ma réponse d'abord, et à partir d'elle discuter de vos résultats à nodgim et toi :

Voici un schéma de support, j'ai repris les noms des points d'enigmatus et dessiné uniquement la section de la sphère des résultats par le demi-plan passant par les 3 points O, C et M.



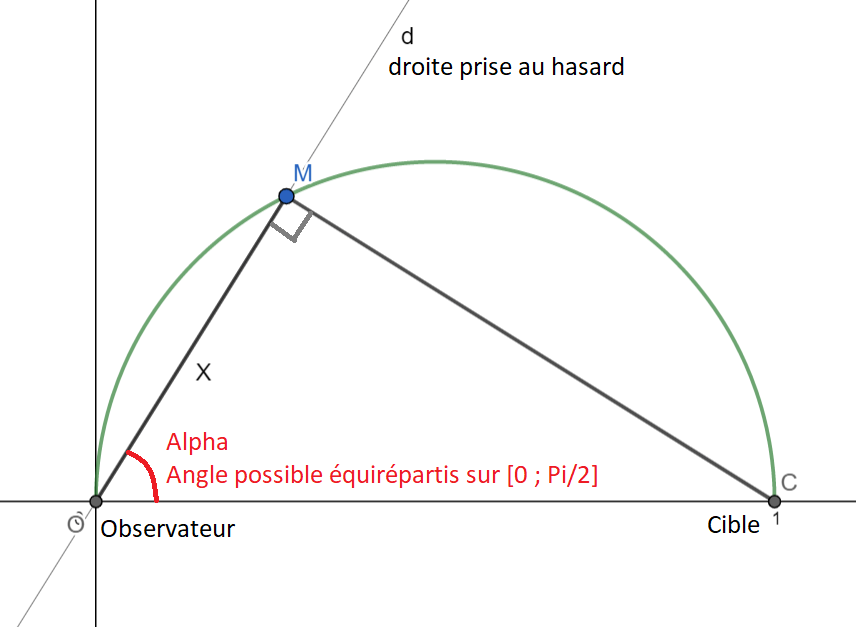
Tous les points M se trouvent sur le demi-cercle de centre 1/2 et de rayon 1/2 (@enigmatus, c'est bien 1/2 pour toi aussi non ?). Puisque la droite est prise au hasard, les angles possibles alpha sont équirépartis sur [0 ; Pi/2].

On s'intéresse à l'espérance de la longueur MC.
MC = sin(alpha)
La valeur moyenne de MC vaut donc 1/(Pi/2) * somme sur [0 ; Pi/2] de sin(alpha) d_alpha qui donne le résultat :
MC_moy = 2/Pi

@nodgim : Concernant ta solution :
Si tu poses x = OM, alors tu as bien MC = √(1-x²), mais le dx que tu utilises alors dans l'intégrale n'est pas équivalent à un d_alpha :
x = cos(alpha) donc dx = -sin(alpha).d_alpha
Tu récupères en plus un facteur -sin(alpha).
En fait l'équirépartition des aphas ne correspond pas à une équirépartition des x.



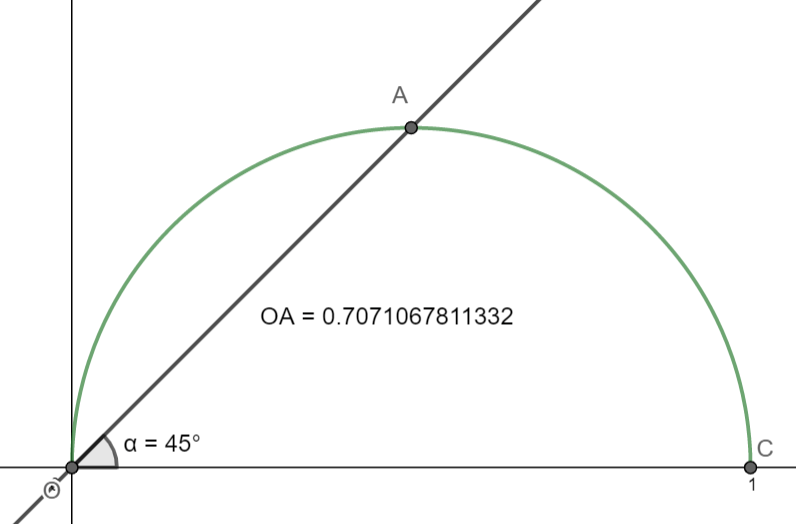
Sur ce 2ème schéma, on voit que pour Alpha entre 0 et Pi/4, donc la moitié des angles, x varie entre 1 et √2/2 et pas entre 1 et 1/2. Du coup, la valeur moyenne de la fonction qui donne la longueur de MC change si tu ne tiens pas compte de ce facteur.

Ta façon de calculer MI ne fonctionne donc pas, et le résultat que tu obtiens donne la valeur moyenne de la courbe représentée en vert ci-dessous alors qu'on cherche celle de la courbe orange (j'ai ramené sur [0;1] la courbe des sinus pour mieux comparer visuellement).



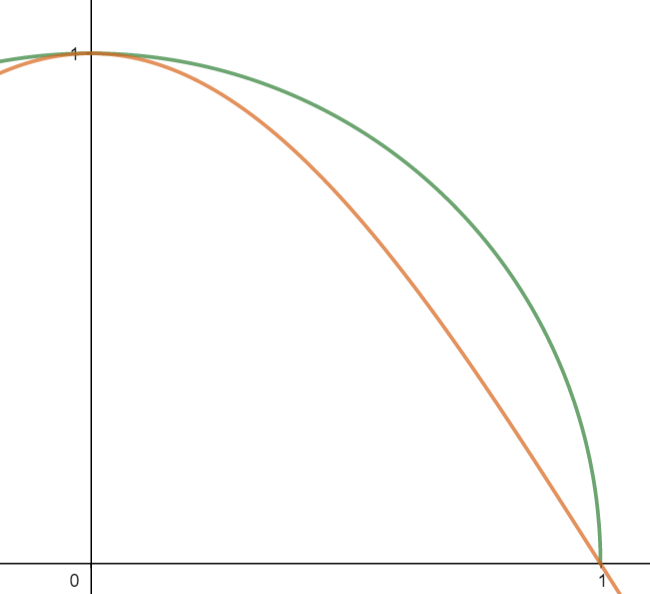
@ enigmatus : Le soucis me semble être le même...

EDIT : Désolé nodgim, je n'avais pas vu ta réponse avant de poster. La réponse 1 - 2/Pi correspond à la distance "gagnée", alors que 2/Pi à la distance restante. J'ai accepté les 2.
Je pense que ta façon de voir les différentes versions est effectivement bonne, par contre une seule est correcte si on se réfère à l'énoncé tel qu'il est posé.

golgot59 #23 a écrit:

Tous les points M se trouvent sur le demi-cercle de centre 1/2 et de rayon 1/2 (@enigmatus, c'est bien 1/2 pour toi aussi non ?). Puisque la droite est prise au hasard, les angles possibles alpha sont équirépartis sur [0 ; Pi/2].

Non, mes points M sont équirépartis sur une sphère de centre O et de rayon OC (du moins la demi-sphère située du côté de C).

L'aire de la portion de sphère située entre 2 plans parallèle distants de H est : 2*pi*R²*H

Pour que les points M soient équirépartis sur la surface de la sphère, il faut que leurs projections P sur OC soient équiréparties sur OC.

Pour moi, dire que les angles alpha sont équirépartis sur [0;pi/2] revient à raisonner dans le plan.

Il faudrait préciser ce que veut dire cette phrase : "Si une droite aléatoire de l'espace passe par votre position"