 |
#1 - 14-10-2024 14:49:52
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
legos stablzs
Une petite question "semi-ouverte" inclassable.
Je dispose de pièces de Lego, des briques en forme de parallélépipède rectangle, de taille 1x1x6 comme celle-ci 𓏠
Lexique :
* Les plots sont les petits ronds sur le dessus des pièces de Lego
* Une structure est un assemblage d'une ou plusieurs pièces
* Une structure "stable" est une structure qui n'a pas de jeu.
* Une structure en une dimension est contenue dans un solide de la forme 1x1xA
* Une structure en deux dimensions est contenue dans un solide de la forme 1xAxB
* Une structure en trois dimensions est contenue dans un solide de la forme AxBxC
Il est tout à fait possible de créer une structure stable en une dimension : une seule brique suffit -- c'est d'ailleurs la seule structure stable à une dimension.
En deux dimensions, deux briques suffisent, l'une au-dessus de l'autre, à condition que la surface de recouvrement soit d'au moins deux plots. Avec un seul plot, il y a du jeu : on peut faire tourner la pièce du dessus autour du plot.
Mais en trois dimensions ?
* Si on essaye de faire un carré creux par exemple, de taille 6, avec deux côtés opposés situés au dessous et les deux autres au-dessus, on peut transformer ce carré en losange en faisant pivoter les pièces
* Si on fait une "croix" : deux barres cote à cote verticalement au dessous, deux autres au dessus, qui se coupent sur la surface centrale 2x2, c'est déjà plus stable... mais il y a encore du jeu (si si essayez vous verrez).
* Même avec un carré de 12 barres, 6 en dessous et 6 au dessus de manière transverse, on aura le même jeu
Question : est-il possible de faire une structure stable en 3 dimensions ? et si oui, combien de pièces faut-il au minimum ?
#2 - 14-10-2024 17:25:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,047E+3
legos stzbles
5, à mon avis.
Ton carré déformé en losange peut être solidifié par une barre sous la forme de deux triangles équilatéraux.
On peut aussi former un rectangle de 3x4 avec deux barres dessous, et deux dessus, solidifié par une barre de 5 ( merci Pythagore ) même si les barres dépassent.
Ces deux solutions utilisent le principe des structures triangulaires et sont en théorie solides (merci M Eiffel)
#3 - 14-10-2024 19:07:35
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Legos tsables
Je pense que cinq pièces, réparties sur trois étages doivent suffire.
Le quatre premières pièces forment un losange sur deux étages. La cinquième relie deux angles opposés du losange.
#4 - 14-10-2024 20:52:50
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 649
- Lieu: Ville 2/N près 2*i
Lego stables
Super énigme, et je confirme que la croix garde du jeu. c'est du vécu ! 
2 pièces : pas possible
3 pièces : il faudrait faire un triangle mais la 1e et la 3e ne sont pas à des niveaux compatibles.
4 pièces : on peut obtenir une structure stable en formant un trapèze :
plots 2 et 5 pris
_ _____ _
/_____\
plots 1 et 6 pris
Bisàtous !
[edit] ah ben zut, non ! Ca pivote toujours, mais si j'ajoute une barre Légo, j'arrive à bloquer la structure avec 5.
plots 1 4 et 6
_____
\_/__\
plots 1 3 et 6
#5 - 14-10-2024 20:58:02
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,047E+3
Legos stabls
EDIT, on peut faire le triplet 3 4 5 avec seulement 4 briques en en soudant 2 sur une des longueurs.
Si on soude deux barres avec 2 plots, on peut même faire n'importe quel triangle jusqu'à 8x5x5
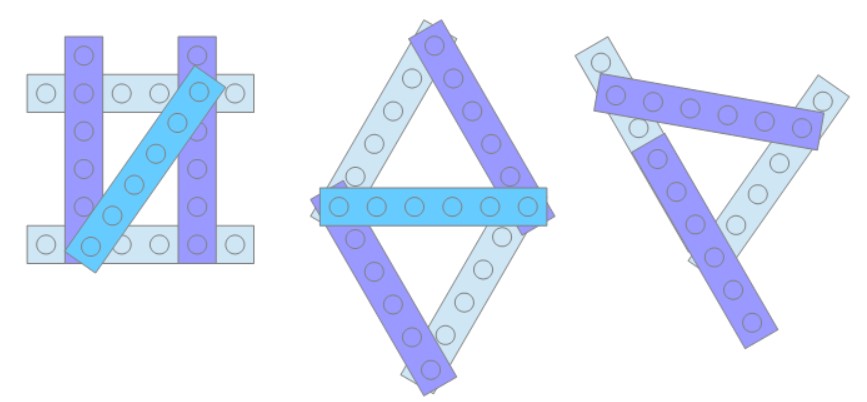
Difficile de faire moins, sauf si :

#6 - 14-10-2024 21:20:01
- Spirou
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 489
megos stables
On peut reprendre la structure stable en deux dimensions, en superposant une pièce au dessus de l'autre, avec deux plots recouverts. Puis, sous la pièce du haut, il est possible de placer une troisième pièce perpendiculairement.
Si cette pièce est collée à celle du bas, il est impossible de la faire pivoter. D'où une structure stable de 3 pièces.
Une autre possibilité est de construire un rectangle de taille 4x3, puis de placer une pièce obliquement pour fixer la longueur de la diagonale (afin d'éviter que la structure soit déformée en losange)
#7 - 15-10-2024 17:35:21
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Legoos stables
Spirou, ta première structure serait bonne sur le papier.
Mais en pratique... non. Il y a toujours un peu de jeu (moins, mais du jeu quand même)
#8 - 15-10-2024 19:49:30
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
legps stables
Un triangle ne marcherait pas car il y aurait toujours deux barres au même niveau qu'on ne pourrait pas joindre.
Mais pourquoi pas un trapèze avec quatre barres: deux disposées en parallèle dessous et deux "inclinées" suivant ce que permet le jeu disposées symétriquement dessus ?
#9 - 16-10-2024 02:31:45
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
legos syables
Franky : essaye si tu as ce qu’il faut. Sinon crois moi : ça bouge encore beaucoup
#10 - 16-10-2024 07:08:04
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 649
- Lieu: Ville 2/N près 2*i
Legos stablse
Cogito lego sum :-)
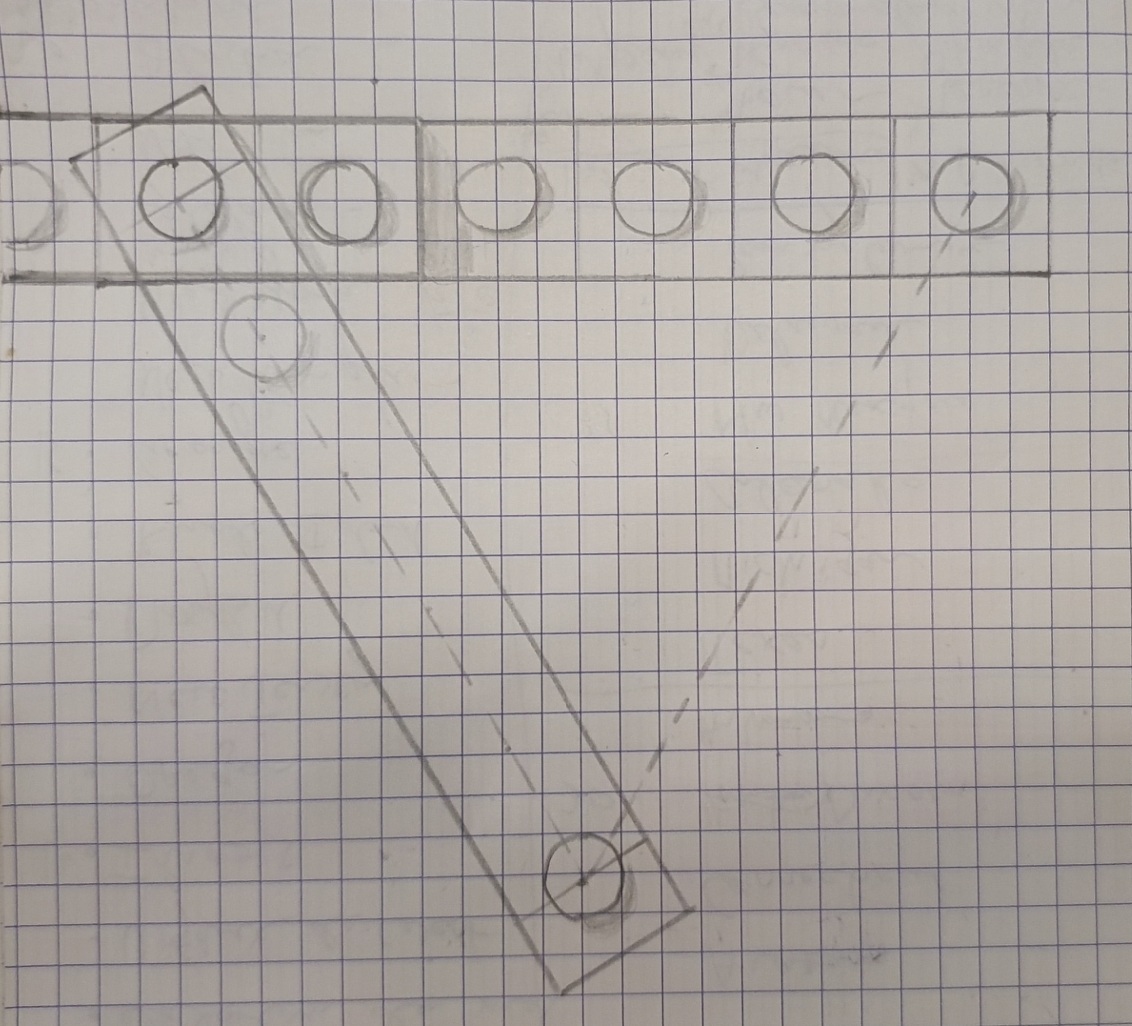
je pense que j'ai trouvé une solution stable en 4 sous forme de triangle. L'un des côtés est constitué de deux barres solidaires d'une longueur totale de 10.
/ \
/ __ \
plots 3 et 8
Ca nous fait un triangle equilatéral. Reste à voir si un angle de 60° est supporté par les barres lego. Je n'ai pas de légos sur moi, mais ce dessin semble montrer que ca passe à l'aise.
#11 - 16-10-2024 19:37:22
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,047E+3
Legos stbles
Des commentaires sur les trucs "invalides", c'est bien, mais cela veut dire que les autres le sont ? (pas invalides, valides, bien sur )
#12 - 18-10-2024 22:25:18
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1083
- Lieu: Nicastro / Tronville
egos stables
Réponse : non
Ceci dit, j'ai un doute
(sans rapport avec mon approche de l'énigme)
tes réponses Scarta, semblent indiquer qu'il y a une solution.
PS : dans l'énoncé, après "celle-ci" , y a-t-il une image qui doit s'afficher, je ne vois rien.
Lélio Lacaille - Du fagot des Nombreux
#13 - 19-10-2024 10:27:29
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 649
- Lieu: Ville 2/N près 2*i
Lego sstables
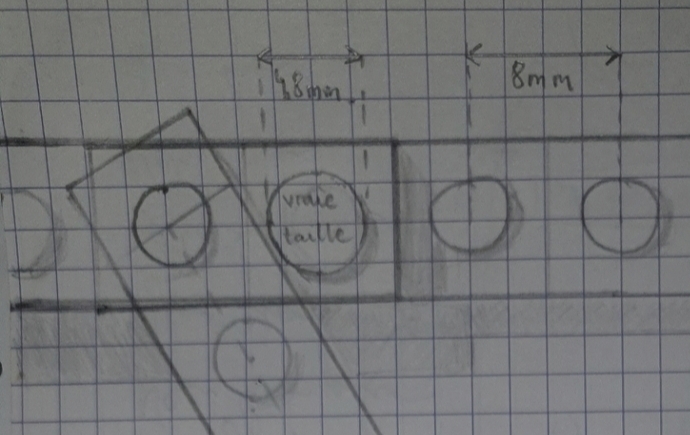
Un petit retour sur mon dessin, j'avais dessiné des plots un peu petits (de mémoire) mais ca passe quand même avec les dimensions officielles (plots de 4,8mm et espacements entre plots de 8mm).
#14 - 19-10-2024 23:10:38
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Legoos stables
Oui la plupart des solutions proposées sont valides sauf celle que je mentionne. Pour la solution de Migou à 4, très interessante. Dès que j’ai des briques sous la main je teste !!
Mais sur le papier c’est correct (et j’avoue que ça résoud élégamment le paradoxe posé par gwen27)
#15 - 19-10-2024 23:12:24
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Legos stabls
@aunryz non ce n’est pas une image mais un caractère Unicode « barre de lego par 6 ». Si si ça existe
#16 - 22-10-2024 14:47:34
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 649
- Lieu: Ville 2/N près 2*i
Legos sstables
Je doiq être un peu obsédé par le problème mais j'ai calculé que l'inclinaison maximale pour un croisement de deux blocs est de 38,0475°
Ca valide le triangle équilateral qui a beso8n de 30° d'inclinaison.
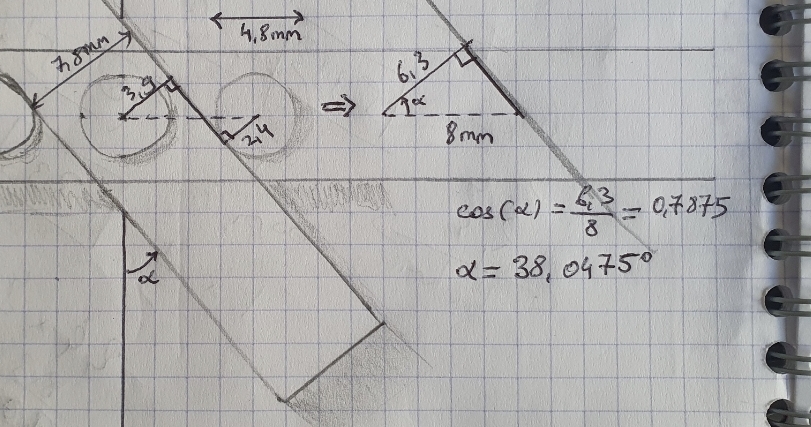
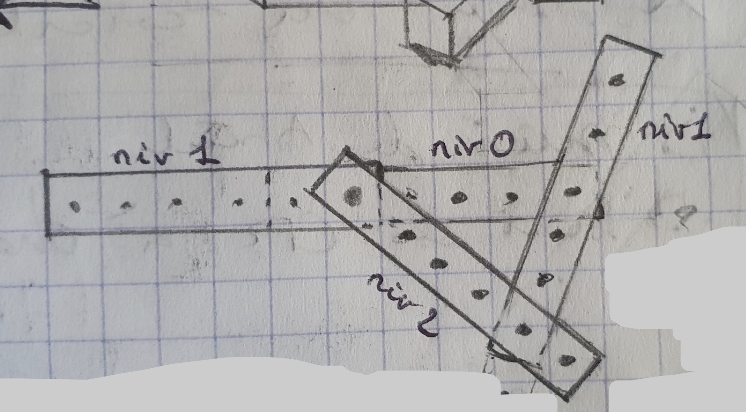
Je viens de penser aussi qu'en positionnant la barre oblique du niveau 2 au rebord de la barre de niveau 1, on obtient plus de liberté de mouvement, ce qui permet de faire divers triangles comme celui-ci.
#17 - 24-11-2024 11:08:51
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
legos stableq
j'avais oublié de venir remercier les participants (moindre des choses quand meme)
Les structures stables à 5 (que j'avais imaginée aussi) sont sous la forme de deux triangles équilatéraux avec une base commune (ou un losange avec une diagonale quoi comme le dit JackV)
Je n'avais pas pensé à la solution à 4 proposée par migou et gwen27 : très joli ! Bravo !
|
 |

 Accueil
Accueil
 Forum
Forum












