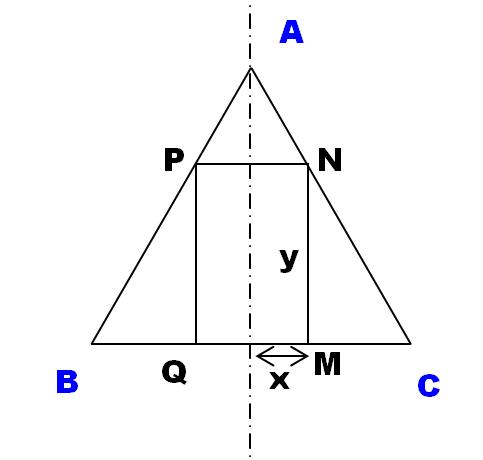
J'ai mis la figure comme proposé par Mathias. J'appelle d la demi-longueur d'un coté (d=6).
L'aire du rectangle est : A(x) = QM * MN = 2x * y
Dans le triangle rectangle MPC, l'angle en C vaut 60°, donc MP/MC=tan (60°) donc y / (d - x) = rac(3), donc y = rac(3) * (d - x).
D'où A(x) = 2 rac(3) x (d - x)
Pour trouver la valeur de x qui maximise A, on peut dériver ou alors judicieusement écrire la valeur de A...
A(x) = 2 rac(3) (xd - x²)
A(x) = 2 rac(3) (-x² + 2 x d/2 - (d/2)² + (d/2)²)
A(x) = 2 rac(3) (-(x-d/2)² + (d/2)²)
De cette expression (somme de 2 termes positifs ou nuls), on trouve que A(x) est maximale pour x = d/2 et que l'aire du rectancgle est alors d²/2 * rac (3).
Pour d=6, les dimensions du rectangle sont donc QM = 6 et MN = 3 rac(3), son aire est 18 rac(3).
Voilà qui répond au problème, cependant, nous sommes partis d'hypothèse a priori qui consiste à dire que les 4 sommets du rectangle appartiennent aux côtés du triangle. C'est intuitif, finalement pas si simple à montrer.
rem : l'énoncé dit "rectangle inscrit dans le triangle" donc si on entend par triangle les 3 segments reliant les sommets, la question ne se pose pas, c'est obligatoire, mais si on entend par triangle la surface sous-tendue par les sommets, on peut s'attacher à le démontrer !
1. Etape 1 : A partir d'un rectangle n'ayant qu'un point (M) en sur un coté du triangle, on peut toujours construire un rectangle plus grand.
Dem : Par un simple homothétie de centre M, on peut faire "grossir" le rectangle jusqu'à toucher un bord.
2. Etape 2 : A partir de tout rectangle n'ayant que 2 points appartenant au triangle, il est facile de construire un rectangle plus grand.
Dem :
Si les 2 points (M et N) sont sur le même coté, alors une homothétie de centre M va faire grossir le rectangle jusqu'à toucher un autre bord, en conservant N sur le coté du triangle
Si les 2 points (M et un autre R) sont sur des cotés différents.
Il est impossible qu'un des sommets du rectangle soit un sommet du triangle (car angle à 60° < 90°).
On translate le rectangle parallèlement au coté portant M dans le sens qui fait rentrer l'autre sommet R dans le triangle. Ce rectangle translaté n'a plus qu'un point en commun et on est ramené à l'étape 1.
3. Etape 3 : A partir d'un rectangle ayant 3 points (MNP) appartenant aux côtés du triangle, il est possible de construire un rectangle plus grand.
Demo :
Si 2 points son sur un même coté, on fait une translation du rectangle le long de ce coté, pour faire rentrer le 3ème dans le triangle, et on est ramené à l'étape 2.
Si tous les points sont sur un côté différent, j'ai pas encore trouvé !!! Je reviens.

 Accueil
Accueil
 Forum
Forum








