 |
#1 - 30-01-2011 22:56:41
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
Les 97 tableaux !!
Une groupe de personnes de nombre [latex]n[/latex] ont visité une musée qui comporte 97 tableaux !
On suppose que tous les tableaux ont été vus et qu'il n'existe pas une personne qui a vu tous les tableaux à la fois .
Montrez logiquement qu'il existe deux personnes : P1 et P2 et deux tableaux T1 et T2 tels que P1 a vu T1 et n'a pas vu T2 ;et P2 qui a vu T2 et n'a pas vu T1 .
Bonne chance !
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#2 - 31-01-2011 03:11:44
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Les 97 tableax !
J'ai fait une preuve par l'absurde, qui m'a mené à construire une suite strictement croissante de graphes inclus dans le graphe total, d'où une contradiction puisque ce dernier est fini.
Intéressant en tout cas ! Merci. Ça vient d'où ?
Notations : Soit [latex]P=(p_1,...,p_n)[/latex] l'ensemble des personnes, [latex]T=(t_1,...,t_{97})[/latex] celui des tableaux.
On note [latex]<p_i,t_j>[/latex] si "[latex]p_i[/latex] a vu [latex]t_j[/latex]" et [latex][p_i,t_j][/latex] sinon.
On note [latex]N(p)[/latex] l'ensemble des tableaux Non vus par [latex]p[/latex], et [latex]V(t)[/latex] l'ensemble des personnes qui ont Vu [latex]t[/latex].
Tout ça donne un graphe (bipartite) non-orienté : [latex]G=(P,T,U=N\cup V)[/latex].
Hypothèses du problème :
i) [latex]\forall p\in P: N(p)\neq \emptyset[/latex] (personne n'a vu tous les tableaux)
ii) [latex]\forall t\in T: V(t)\neq\emptyset[/latex] (tous les tableaux ont été vus)
iii) (par l'absurde) : [latex]\not\exist p,p'\in P,t,t'\in T: p\in V(t)\wedge p'\in V(t')\wedge t'\in N(p)\wedge t\in N(p')[/latex]
Définition de la suite de graphes croissants :
Par récurrence, on définit [latex]G_i=(P_i,T_i,N\cup V)[/latex] et on assure par construction que chaque [latex]G_i\subset G[/latex] et vérifie l'invariant :
[TeX]\Phi(i)=\forall j\in\{1,..,i\}: (\forall k\in\{1..j-1\}: [p_j, t_k]\wedge \forall k\in\{j..i\}: <p_j, t_k>)[/TeX]
En particulier, dans [latex]G_i[/latex], personne n'a vu [latex]t_i[/latex].
Initialisation de la définition :
On commence avec [latex]G_1[/latex]: soit [latex]p_1\in P[/latex] ([latex]P[/latex] est non-vide) et soit [latex]t_1\in N(p_1)[/latex] (un tel [latex]t_1[/latex] existe d'après ii), soit alors [latex]G_1=(\{p_1\},\{t_1\},N\cup V)[/latex], on vérifie facilement que [latex]G_1[/latex] vérifie [latex]\Phi(1)[/latex].
Étape de récurrence :
Hypothèse de récurrence : [latex]G_i[/latex] satisfait [latex]\Phi(i)[/latex]
Or [latex]V(t_i)[/latex] ne peut être dans [latex]P_i[/latex] sinon contradiction avec [latex]\Phi(i)[/latex]. Soit donc [latex]p_{i+1}\in V(t_i)[/latex].
On vérifie (1) que [latex]\forall t_j\in T_i: <p_{i+1},t_j>[/latex], donc [latex]N(p_{i+1})\neq \emptyset[/latex]. Soit [latex]t_{i+1}\in N(p_{i+1})[/latex], on l'a vu [latex]t_{i+1}\not\in T_i[/latex] c'est donc un nouveau tableau à considérer.
On vérifie (1) que [latex]\forall p_j\in P_i: [p_j,t_{i+1}][/latex]
On pose [latex]P_{i+1}=P_i\cup\{p_{i+1}\}[/latex] et [latex]T_{i+1}=T_i\cup\{t_{i+1}\}[/latex] et [latex]G_{i+1}=(P_{i+1},T_{i+1},N\cup V)[/latex]
et on conclut que :
- [latex]G_i\subset G_{i+1}\subset G[/latex]
- [latex]G_{i+1}[/latex] vérifie [latex]\Phi(i+1)[/latex] : donc on peut recommencer, ad nauseam...
Or [latex]G[/latex] étant fini, on aboutit à une contradiction.
(1) je zappe les détails mais l'idée est que sinon, on trouverait le quadruplet [latex]p,p',t,t'[/latex] qu'on suppose ne pas exister.
#3 - 31-01-2011 14:01:28
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Les 97 atbleaux !
Azdod, tu as une solution simple ne faisant pas appel à un résultat "connu" ?
#4 - 31-01-2011 14:05:38
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
les 97 tablezux !
gasole : je crois que c'est possible avec le denombrement ! ta demonstration est géniale !
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#5 - 31-01-2011 14:28:20
- debutant1
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 116
led 97 tableaux !
soit p1 l"ensemble des personnes ayant vus t1.
une personne de p1 n'a pas vu t2
soit p2 l'ensemble des admirateurs de t2.
si la proposition est fausse p2 est inclus dans p1.
on recommence avec tous les tableaux non vus par des personnes de p1 et conclusion, tous les ensembles pn sont donc inclus dans p1.
comme tous les tableaux sont vus par au moins une personne ,on voit que tous le monde appartient à t1. ce qui est contraire à l’hypothèse. donc la proposition est juste pour au moins une personne.
#6 - 31-01-2011 14:31:17
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
les 97 tableayx !
@azdod : ... malgré quelques abus de notation à des fins d'allègement 
mais où as-tu trouvé ça ? je m'en resservirai et mes étudiants vont te maudire
#7 - 31-01-2011 14:36:42
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
Les 97 tableaux
 Lol dans un concours des olympiades des maths que j'ai deja passé ! mais dommage que je n'ai pas réussi a la résoudre ce jour là 
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#8 - 31-01-2011 15:31:30
- logan
- Passionné de Prise2Tete
- Enigmes résolues : 47
- Messages : 90
Les 9 7tableaux !
Bon ben moi j'utiliserais bien un raisonnement par récurrence
Au niveau 1 (ie. deux personnes)
- On sait qu'autant des deux n'a vu tous les tableaux
- Que tous les tableaux ont été vu
-> chacun des visiteur n'a pas vu au moins un tableau et ça ne peut pas être le même --> la condition est respecté
Faisons l'hypothèse que c'est vrai pour N personnes, est ce vrai pour N+1 personnes ?
Si vrai au niveau N on a un couple (Arnold et Willy) de deux personnes qui vérifié la condition. Avec une personnes en plus (un retardataire LOL) on aura toujours le même couple de personne (toujours Arnold et Willy) pour qui la condition est respectée.
Voila voila (je ne suis pas trop sûr de moi mais bon)
#9 - 31-01-2011 17:05:23
- irmo322
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 203
lzs 97 tableaux !
Une petite démo par l'absurde:
Alors supposons par l'absurde que qu'il n'existe pas 2 personnes P1 et P2 et deux tableaux T1 et T2 tels que P1 a vu T1 et pas T2 et P2 a vu P2 mais pas P1.
Soit <= la relation d'ordre sur l'ensemble des personnes telle que:
Si P1 et P2 deux personnes telles que P1<=P2, alors P2 a vu (au moins) tous les tableaux qu'a vu P1.
Grâce à ce qu'on a supposé par l'absurde, <= est une relation d'ordre totale.
Il existe donc dans l'ensemble fini des personnes un élément maximal pour <=.
Comme tous les tableaux ont été vus, l'élément maximal a vu tous les tableaux. Contradiction!
Ainsi il existe deux personnes : P1 et P2 et deux tableaux T1 et T2 tels que P1 a vu T1 et n'a pas vu T2 ;et P2 qui a vu T2 et n'a pas vu T1 .
#10 - 31-01-2011 17:50:51
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
les 97 tableauw !
Tant que chaque tableau a été vu par au moins deux personnes, je vire une personne.
Au bout d'un moment, au moins un tableau T1 n'a été vu que par une seule personne P1.
Cette personne n'a pas pu vu au moins un autre tableau T2 qui a été vu par une des autres personnes restantes P2.
#11 - 31-01-2011 18:53:00
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,014E+3
Less 97 tableaux !
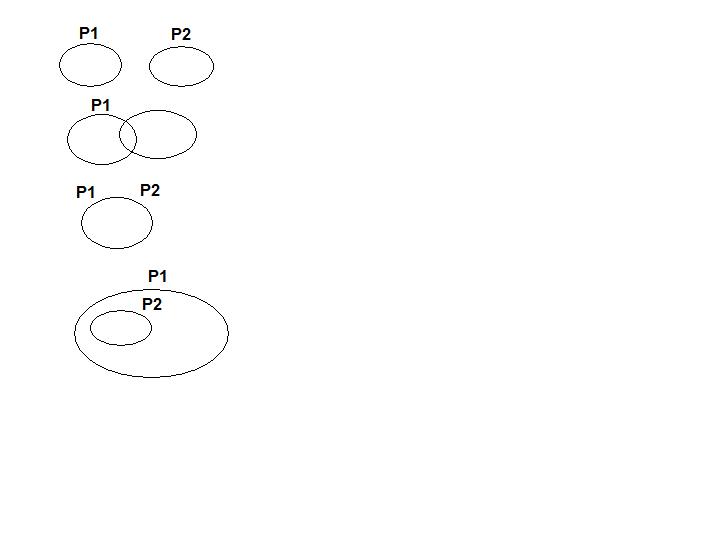
Premier cas possible: je trouve deux personnes ayant vu des tableaux différents l'un de l'autre ou bien deux personnes ayant vu des tableaux en commun mais pas tous. ( voir les deux premiers dessins) Alors, il est facile de trouver T1 et T 2.
Imaginons que ce ne soit pas le cas... Alors chacun des n visiteurs appartient à une des deux autres configurations.
Second cas possible donc: L'ensemble des tableaux vu par P1 comprend l'ensemble des tableaux vus par P2 ( ou le comprend exactement ).
Dans ce cas, il existe une personne qui a vu le plus de tableaux Pn Mais dans cette configuration, soit Pn a vu tous les tableaux, soit tous les tableaux n'ont pas été vus : cas impossible.
Il existe donc au moins deux personnes correspondant au premier cas étudié.
#12 - 31-01-2011 19:16:39
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
Les 97 tableux !
bravo à tous chacun a démontré de sa façon encore un bravo
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#13 - 01-02-2011 19:50:09
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
les 97 tzbleaux !
Je vais essayer... Même si encore une fois je trouve que j'ai fait bien compliqué.
Pour l'instant je ne me préoccupe pas de la valeur de n.
Je prends le tableau T1. Il a été vu au moins une fois, notons P1 une des personnes qui l'a vu.
P1 n'a pas vu tous les tableaux, donc il existe T2 tableau que P1 n'a pas vu.
Et comme T2 a été vu au moins une fois, il existe P2 qui a vu T2
Maintenant, 2 possibilités :
- P2 n'a pas vu T1, et on a trouvé nos P1,P2,T1,T2
- P2 a vu T1
C'est là que j'utilise un tableau qui prend en entrée les tableaux et les personnes, et un 1 signifie que P a vu le tableau T, un 0 le contraire :
T1 T2
P1 1 0
P2 1 1
On continue : P2 n'a pas vu tous les tableaux, donc il existe T3 que P2 n'a pas vu
T1 T2 T3
P1 1 0
P2 1 1 0
Si P1 a vu T3, on conclut avec P1,P2,T2,T3
Si P1 n'a pas vu T3, alors T3 n'a été vu ni par P1, ni par P2. Mais comme il a été vu au moins une fois, on a une P3 qui a vu T3
Si P3 n'a vu T1 (ou pas vu T2), on conclut avec P1 (ou P2), T1 (ou T2), P3, T3
Reste donc le cas où P3 a vu et T1 et T2
T1 T2 T3
P1 1 0 0
P2 1 1 0
P3 1 1 1
De la même manière, il existe T4 que P3 n'a pas vu
T1 T2 T3 T4
P1 1 0 0
P2 1 1 0
P3 1 1 1 0
On peut conclure sauf si T4 n'a été vu par aucun des P1,P2,P3
On se retrouve alors avec
T1 T2 T3 T4
P1 1 0 0 0
P2 1 1 0 0
P3 1 1 1 0
On itère le processus, jusqu'à épuiser soit les tableaux soit les n personnes
Si n >= 97
T1 T2 T3 T4 ... T97
P1 1 0 0 0 ... 0
P2 1 1 0 0 ... 0
P3 1 1 1 0 ... 0
... ... ... ... ... ... ...
P96 1 1 1 1 ... 0
P97 1
Comme P97 ne peux pas avoir tout vu, il y a un tableau qu'il n'a pas vu, Tx, et on peut conclure avec Px,P97,Tx,T97
Si n < 97
T1 T2 T3 T4 ... Tn+1
P1 1 0 0 0 ...
P2 1 1 0 0 ...
P3 1 1 1 0 ...
... ... ... ... ... ... ...
Pn 1 1 1 1 ... 0
Comme Tn+1 doit être vu, c'est forcément par un Px (il ne reste plus personne d'autre qui peut avoir vu Tn+1), et on conclut avec Px,Tx+1,Pn,Tn+1
Je ne me sers jamais de la valeur 97, donc j'imagine qu'il y a une astuce ...
#14 - 01-02-2011 21:41:06
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Les 97 taableaux !
Traduction de l'énoncé :
(1) Pour tout tableau Ti, il existe au moins une personne Pj telle que Pj a vu Ti.
(2) Pour toute personne Pm, il existe au moins un tableau Tn tel que Pm n'a pas vu Tn.
Faisons un démonstration par récursion...
Et puis non, je crois qu'il y a plus simple : parlons d'ensembles.
(1) U Tj (union des tableaux vus par chacun) = E (ensemble des tableaux)
(2) Pour tout Pj, Tj (ensemble des tableaux qu'il a vus) <> E
D'après (1) et (2), il n'existe pas de Tj tel que Tj contienne tous les autres Ti. Sinon il vaudrait E.
Prenons Ti et Tj 2 ensembles de tableaux qui ne se contiennent pas l'un ou l'autre. Autrement dit, Tj possède une intersection avec le complémentaire de Ti.
Ainsi Tj contient au moins 1 tableau n'appartenant pas à Ti. Et réciproquement.
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#15 - 03-02-2011 10:36:40
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
es 97 tableaux !
Logan ta récurrence ne marche pas. Elle ne couvre pas tous les cas possibles.
Les ensembles de tailles N+1 que tu couvres sont ceux dont il existe un sous-ensemble de taille N de personnes qui ont déjà vu tous les tableaux, ce qui ne représentent pas tous les cas possibles.
Je pense que précisément tu montres que la propriété est vrai pour tout ensemble de n personnes où deux personnes ont vu tous les tableaux à elles seules.
Il faudrait plutôt dire que si tu as un ensemble de taille N+1 alors il y a deux cas possibles :
1) Il existe un sous ensemble de taille N où tous les tableaux ont été vu : Ok par récurrence ( le cas que tu fais)
2) Il n'existe pas de sous ensemble de taille n ou tout le monde a vu tout les tableau. => Il existe un tableau T1 qu'une seule personne P1 a vu. Cette personne a pas vu au moins un tableau T2 qu'au moins une personne P2 a vu.
=> gagné (le cas que tu ne couvres pas)
En fait la preuve que j'ai faite en plus formelle ^^
#16 - 03-02-2011 11:45:59
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Les 97 tableaaux !
J'aime beaucoup la preuve de fix33... Simple, claire et efficace.
@irmo : Irmo, tu t'es gourré, l'ordre n'est pas total.
#17 - 03-02-2011 14:34:50
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
es 97 tableaux !
Le fait que deux personnes puissent chacune avoir vu un tableau que l'autre n'a pas vu rend l'ordre partiel.
Donc dans son raisonnement par l'absurde l'ordre est bien total.
#18 - 03-02-2011 15:29:23
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
lzs 97 tableaux !
Exact Nicouj, j'ai parlé trop vite.
Grrr ... J'aurais dû réfléchir plus avant de me jeter dans une récurrence, du coup j'ai pas vu que l'hypothèse du raisonnement par l'absurde implique que [latex]T(P1)\subseteq T(P2)[/latex] ou [latex]T(P2)\subseteq T(P1)[/latex] qui est précisément l'axiome de linéarité.
Mots clés des moteurs de recherche
|
 |
Accueil
