|
#1 - 13-03-2011 14:13:17
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
aiee, segment et prise de tête !
Imaginez un segment [AB] de longueur 1 situé sur un plan.
Il faut réussir à retourner ce segment de telle sorte que B prenne la place de A et inversement. Tout doit se faire dans la dimension du plan. Et le segment ne peut pas être altéré d'aucune façon que ce soit.
Toute surface balayée par le segment est colorée.
Quelle est la plus petite aire qu'il faut au final colorer ?
(un descriptif même succinct de la forme sera bienvenu !)
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#2 - 13-03-2011 14:22:49
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Aire, segment et prisee de tête !
http://enigmusique.blogspot.com/
#3 - 13-03-2011 14:38:30
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
aire, segment et prisz de tête !
π4, en faisant faire au segment une rotation dont le centre est le milieu du segment ?
#4 - 13-03-2011 14:40:29
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
aiee, segment et prise de tête !
Au début, j'avais proposé 3π16≈0.589 avec une demi astroïde.
(système "porte d'autobus")
Halloduda a pour l'instant trouvé la meilleure solution !!
Mais il y a mieux encore mieux...
Oui, il y avait mieux :
L'aire minimale est π8≈0.3927
C'est l'intérieur d'une deltoïde,
http://en.wikipedia.org/wiki/Deltoid_curve
dont le grand cercle a un rayon de 3/4 et le petit cercle un rayon 1/4.
L'aire balayée est S=2π(14)2=π8
Il y a encore mieux ! ZERO ! ou du moins, arbitrairement petit.
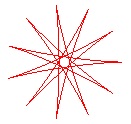
Quand on multiplie le nombre de points de rebroussement à l'infini, la surface de l'hypocycloïde enveloppe du segment tend vers 0.
L'épicycloïde a un diamètre extérieur hors tout inférieur à 2.
Problème dit de Kakeya : comment retourner une aiguille (de longueur 1) dans le plan de sorte qu'elle balaie une aire la plus petite possible ?
Ici, l'aire balayée vaut π8, et on a longtemps pensé que c'était l'aire la plus petite possible ; mais en 1928, Besicovitch a démontré que l'on pouvait retourner une aiguille dans une aire aussi petite qu'on veut.
(d'après http://www.mathcurve.com/courbes2d/delt … toid.shtml)
#5 - 13-03-2011 14:51:45
- thedoums
- Professionnel de Prise2Tete
- Enigmes résolues : 23
- Messages : 223
aire, segment et prise dr tête !
je dirai Pi*0,5^2
ca me parait trop simple pour etre ca...
#6 - 13-03-2011 14:53:56
- guilhem
- Passionné de Prise2Tete
- Enigmes résolues : 27
- Messages : 60
- Lieu: sur Tatouïne, chez Luke
Aire, segment et prise de ttêe !
Pour qu'il y est le moins de détour et de déplacement, ont fait tourner le segment sur lui même autour de sont milieu. Ont a colorier un cercle de rayon 0,5 cm soit
pi*R^2= PI*0,5^2= 0,785398163
l'aire colorier minimale est de 0,785398163 cm2
edit: correction erreur de calcul
#7 - 13-03-2011 16:09:06
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Aire, segment et pries de tête !
Guilhem, tu t'es trompé dans ton explication et dans ton calcul t'emmêlant entre diamètre et rayon.
Halloduda a pour l'instant trouvé la meilleure solution !! 
Mais il y a mieux encore mieux...
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#8 - 13-03-2011 16:22:18
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,093E+3
Aire, segmnet et prise de tête !
#9 - 13-03-2011 17:02:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Aire, ssegment et prise de tête !
Je crois me souvenir qu'on peut retourner le segment dans une aire aussi petite que l'on veut . Je retrouverai les références si personne ne le fait pour moi 
Vasimolo
Et hop http://en.wikipedia.org/wiki/Kakeya_set
#10 - 13-03-2011 17:43:16
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
aire, segment ey prise de tête !
Problème posé par Sôichi Kakeya en 1917, le mathématicien Besicovitch a prouvé en 1928 qu'il existe des ensembles de Kelaya dont la surface pouvait être aussi petite que l'on veut, mais c'est super dur ta question !!! Tié fou ou koi ? 
La forme dans laquelle on travaille ressemble à ça :

voir un article ==> ici
#11 - 13-03-2011 18:23:00
#12 - 13-03-2011 18:57:21
- Memento
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 176
aire, segment ey prise de tête !
Euh, ... 0 ? 
Je ne vais pas voler la vedette au mathématicien qui l'a démontré. Il s'agit de Besicovitch. Le problème s'appelle l'aiguille de Kakeya.
Voici un très bon résumé:
http://math.univ-lyon1.fr/~borrelli/UO/ … _conf4.pdf
#13 - 13-03-2011 19:01:47
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Aire, segment et pries de tête !
Il faut faire mieux qu'un cercle de rayon 0.5 donc une surface de π4≈0.7854
Je propose une forme de voilier avec un tirant d'eau de 0.25
et une surface d'environ 0.643
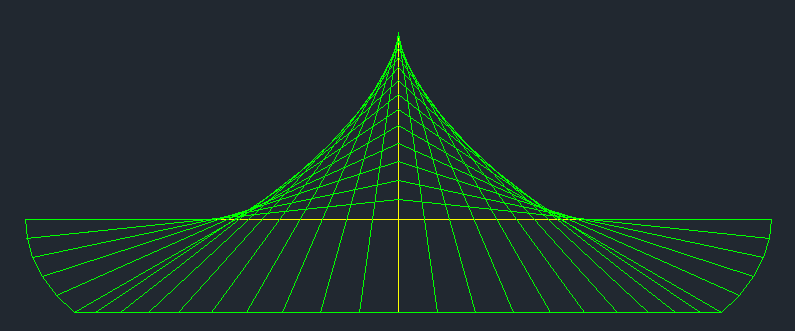
Il est sans aucun doute possible de faire mieux en creusant la coque et en augmentant la taille du mat.
The proof of the pudding is in the eating.
#14 - 13-03-2011 21:18:07
- JBF64
- Amateur de Prise2Tete
- Enigmes résolues : 29
- Messages : 1
Aire, segment et prisse de tête !
On fait tourner le segment en son milieu d'où l'aire balayée PI * AB² /4.
Non ? je me suis trompé ?
#15 - 14-03-2011 01:32:12
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Aire, segment et prise de tête
Je dirais l'aire formé par l'ensemble des segment de taille 1 tangents à un demi-cercle de rayon 1 en leur milieu.
#16 - 14-03-2011 02:42:04
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Aire,, segment et prise de tête !
C'est le problème de Kakeya, dont il a été démontré par Besicovitch que l'on peut colorier une aire aussi petite que l'on veut !
J'avoue que malgré tout ce que j'ai lu là dessus, j'ai encore du mal à visualiser la technique pour y arriver ...
#17 - 14-03-2011 11:57:30
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
aire, segmebt et prise de tête !

Si on suppose R très grand (par exemple de l'ordre de l'infini), alors si le segment AB est d'épaaiseur infinitésimale, la surface à colorier serait proche de 0. Car le segment devient une portion infinitésimale du cercle de rayon R. PAreil pour le cercle de rayon 2R.
#18 - 14-03-2011 14:28:34
- chalibou
- Habitué de Prise2Tete
- Enigmes résolues : 25
- Messages : 16
aire, seglent et prise de tête !
J'avais envie de répondre pi/4, et puis je me suis dit trop évident, il faut surement un truc un peut plus guedin...
Ceci n'est pas à l'échelle:
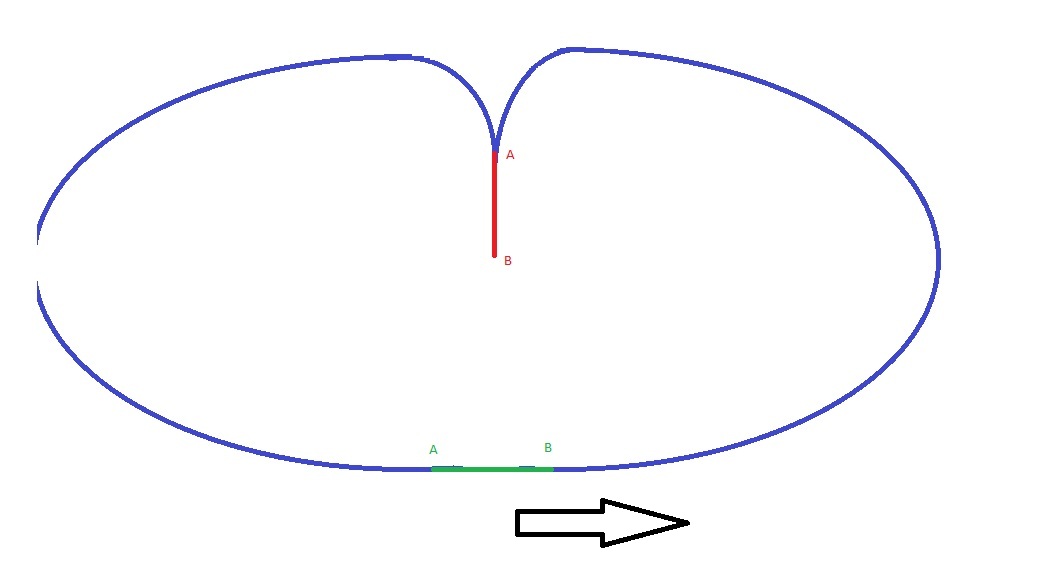
Le segment est en bas, un segment n'a pas de surface, si je le déplace linéairement: la trace n'a pas de surface non plus...
Dans les virages il me suffit de prendre un rayon de courbure très grand (presque infini) pour assimiler la courbe à une droite. Comme je l'assimile à une droite, la trace est une droite et n'a pas de surface... par analogie la terre est de forme ovale (oui) pourtant l'horizon nous apparait bien rectiligne à notre échelle. (j'espère que vous l'avez). Du coup vous faites le pti parcours comme sur le dessin et pi voila vous y êtes... Plus les rayons de courbure sont importants plus la surface balayée est résiduelle.
Donc si on fait pas ca sur une feuille A4 et qu'on peut se balader sur le plan à l'infini je dirais que la surface balayée est quasi nulle.
...voila, c'est assez guedin?
#19 - 14-03-2011 14:54:07
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1984
Aire, segment et pris de tête !
3 étapes
1) On trace la perpendiculaire P à [AB] qui passe par B, ainsi qu'un point B' sur D tel que BB' = 1.
A part en A' = B en suivant la droite AB tandis que B part en B' en suivant la droite (BB')
2) Puis le segment [A'B'] glisse le long de (BB') tour se retrouver avec A' en A'' le symétrique de B' par rapport à B, et B'' sur B
3) Enfin, on fait l'opération inverse de l'étape 1: B'' part en A et A'' glisse sur (BB') pour atteindre B
L'aire de ce truc là est un peu dure à calculer, mais je vais essayer quand même.
On place l'origine du repère en B, (AB) est l'axe des X et (BB') celui des Y
Lors de l'étape 1, quand A se situe aux coordonnées (a;0), B se situe en (0;b)
La distance entre les 2 est de 1, donc b=√1−a2
L'équation de la droite qui les relie est de la forme mx+p. Pour l'ordonnée à l'origine, on a p=√1−a2, et d'autre part ma + p = 0.
On trouve l'équation de la droite D:(a−X).√1−a2a
Ensuite, on s’intéresse à la fonction f qui à X fait correspondre max. Autrement dit, il s'agit du point le plus haut en X parmi toutes les droites qu'on a tracé. Une petite dérivée en a et quelques inéquations nous permettent de trouver une formule pour f : (1-x^{\frac{2}{3}})^{\frac{3}{2}}
Cette fonction ressemble à ça: http://www.wolframalpha.com/input/?i=(1 … rom+0+to+1
Chouette, c'est grosso-modo ce que je recherchais
On vérifie pour être sûr que f(f(x)) = x, en effet on s'attend à une certaine symétrie : si pour une abscisse X, la hauteur est f(X), alors pour une abscisse f(X), la hauteur devrait être X. Il se trouve que c'est bien le cas.
L'intégrale de ce bidule est de 3pi/32
Pour l'étape 2, une droite n'a pas d'aire: 0
L'étape 3 est similaire à l'étape 1, l'aire est donc la même.
L'aire à colorier en utilisant cette méthode est donc de 3Pi/16
#20 - 14-03-2011 14:59:22
- Oups!
- Passionné de Prise2Tete
- Enigmes résolues : 42
- Messages : 58
- Lieu: entre Roazhon et Naoned
Aire, segment et prise de têe !
Bonjour,
En théorie, si l'on fait tendre l'amplitude des mouvements vers l'infini, l'aire balayée tend vers 0 ! (non ! non ! pas factorielle 0)
L'idée est assez simple :
Imaginons qu'une voiture est ce segment, il s'agit donc de faire faire un demi-tour
à ce segment comme nous le ferions avec notre voiture. (Enfin, ceux qui ont une voiture et le permis — ou sont en train de le passer).
1- avancer et tourner à 90° à gauche
2- reculer (d'au moins deux fois la longueur du segment)
3- avancer et tourner à 90° à gauche
Ça marche aussi vers le droite 
Honnêtement, par hasard je suis tombé sur ce problème sur un site très récemment.
Je vais essayer de retrouver l'adresse.
JJ
#21 - 14-03-2011 15:10:30
- LeSingeMalicieux
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1298
- Lieu: Haute-Marne
aire, sehment et prise de tête !
Bon, euh... D'instinct simiesque, je ferais comme ça :
(à chaque étape, on part du segment rouge pour aller au segment bleu).

Mais bon, pour ce qui est de calculer l'aire... Une histoire d'intégrale sans doute...
Avoir quatre mains, c'est plus pratique pour taper sur un clavier.
#22 - 14-03-2011 15:20:08
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
Aire, segment ett prise de tête !
Bonjour
On peut tout d'abord penser à un cercle de diamètre 1 ou à un triangle équilatéral de hauteur égale à 1
mais il y a mieux :
Une deltoïde (roulement d'un cercle de diamètre 1/3 à l'intérieur d'un cercle unitaire ....)
et encore mieux !
(en fait l'aire minimale est aussi petite que l'on veut ....)
Kakeya needle problem : en.wikipedia.org/wiki/Kakeya_set
Argh !
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#23 - 14-03-2011 16:41:34
- Oups!
- Passionné de Prise2Tete
- Enigmes résolues : 42
- Messages : 58
- Lieu: entre Roazhon et Naoned
aire, seglent et prise de tête !
Ça y est ! j'ai fini par remettre la main dessus, non sans mal 
Il s'agit d'une énigme connue sous le nom de "L'aiguille de Kakeya". Elle est très bien expliquée ici :
http://eljjdx.canalblog.com/archives/re … index.html
Par contre, je n'y voit pas d'illustration de ma solution. C'est un peu dans l'esprit de l'exemple avec les points A, B et C mais je ne la comprend pas vraiment. Enfin, bon...
j'ai trouvé cette image pour l'illustration :
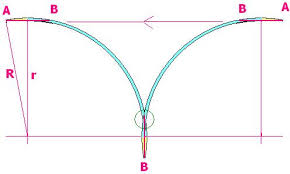
JJ
#24 - 14-03-2011 17:40:37
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Aire, segment et pris de tête !
L'idée est donnée par le schéma suivant dans lequel j'ai dessiné une rotation partielle :
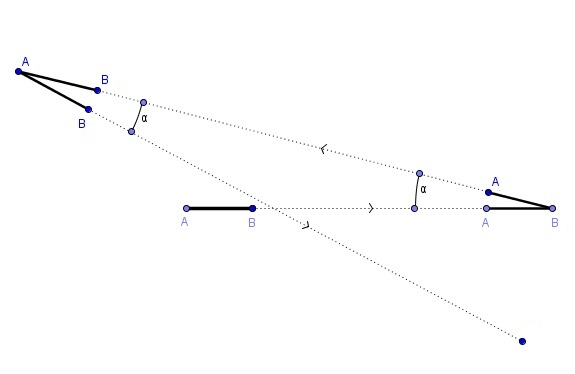
Pendant les mouvements de translation du segment, la surface balayée est nulle, et on s'aperçoit ensuite que les angles \alpha peuvent être rendus aussi petits que l'on veut, il suffit que les rotations \alpha se fassent très loin : je m'éloigne très très loin, je tourne un peu, puis je reviens, et ainsi de suite, jusqu'à me superposer aux points départ.
On subodore donc que la surface finale balayée est aussi petite que l'on veut...
Mais bon, je la connaissais comme je l'ai dit plus haut  dommage, je n'ai pas pu chercher naïvement. dommage, je n'ai pas pu chercher naïvement.
#25 - 14-03-2011 20:04:44
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
aire, segment zt prise de tête !
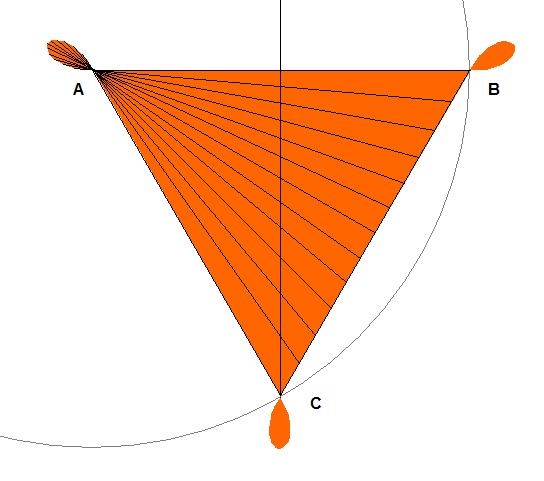
On appelle Am et Bm les extrémité mobiles du segment (A et B étant les positions initiales de Am et Bm)
On construit le triangle équilatéral ABC, on fait glisser le segment le long de BC on le faisant passer par A. On amène ainsi l'extrémité Bm en C. L'extrémité Am est en A.
On fait ensuite de la même façon pour faire passer Am en B, puis Bm en en A.
L'aire balayée est l'aire du triangle ABC augmentée de 3 fois l'aire de la courbe (rosace) engendrée par l'extrémité du segment.
En coordonnées polaires, la rosace est définie par r=1 - cos(t-pi/6), pour t allant de -pi/6 à pi/6, dans un repère bien choisi.
Donc Ar = 1/2 intégrale (r²) pour t allant de -pi/6 à pi/6.
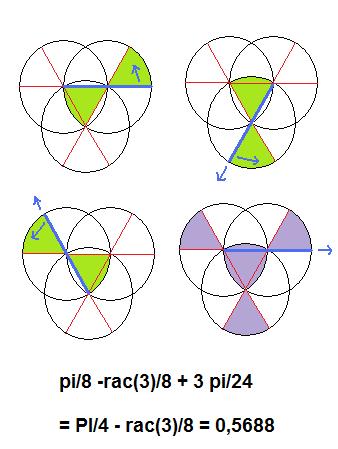
Le calcul donne : Ar = pi/4-1-rac(3)/8
L'aire du triangle est At = rac(3)/4
L'aire totale balayée est A = 3 x Ar + At = 5rac(3)/8 + 3 pi/4 - 3
A.N. A = 0,438726
Je ne sais pas si c'est l'optimum, mais c'est mieux que le disque de rayon 1/2 passant par AB, dont l'aire est pi/4 = 0,785...
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum