Cube 1 : 0 1 2 3 4 5
Cube 2 : 0 1 2 3 4 5
Cube 3 : 0 1 2 6 7 8
Cube 4 : 0 1 6 7 8 -

Rigoureusement, il faudrait deux "9" mais
Il suffit de retourner un 6 si on a besoin d'un 9 non ?

Pour les jours il faut un cube avec les chiffres de 0 à 5 et l'autre avec 0 - 1 - 2 - 6 - 7 - 8  pour le neuf on renverse le 6 

Pour les mois le même cube avec les chiffres de 0 à 5 et un autre avec 0 - 1 - 6 - 7 -  8

Démonstration :

Pour plus de commodités appelons nos cubes Robert et Maurice 

Robert = 0 - 1 - 2 - 3 - 4 - 5     Maurice = 0 - 1 - 2 - 6 - 7 - 8

M  R
0   1
0   2
0   3
0   4
0   5
Hop on change !
R  M
0  6
0  7
0  8
Hop on renverse le 6
0  9   
...
On rechange à 13 et ainsi de suite ...

Et pareil pour les mois 

Et pour ceux qui veulent se prendre la tête tous les matins
http://www.ingramed.net/fig/games/Virtu … us_fr.html

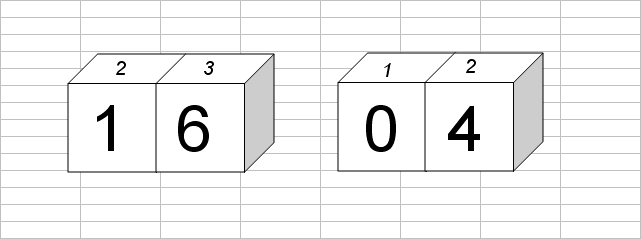
Le jour se compose d'un chiffre des dizaines entre 0 et 3 et d'un chiffre des unités "quelconque" (si les dizaines sont a 3, l'unité sera 0 ou 1).

Le mois se compose d'un chiffre des unités valant 0 ou 1 et d'un chiffre des unités "quelconque" (si les dizaines sont a 1, l'unité est 0, 1 ou 2).

A priori, ça nous donne 26 chiffres a placer sur 24 faces de cubes, mais je ne suis pas sûr que cet embryon de raisonnement permette de dire qu'on ne peut pas s'en sortir avec 4 cubes.

Essayons de développer :

- le 0 devra être au moins sur 2 cubes (exemple : 01/01)
- le 1 devra être sur les 4 cubes pour prévoir le 11 novembre
- le 2 devra être sur 3 cubes (pour le 22 février)
- le 3 sur deux cubes (pour le 3 mars par exemple)
- idem pour le 4, le 5, le 6, le 7, le 8, le 9 (4 avril, 5 mai...)

Ce qui nous donne 23 faces occupées alors qu'on en a 24 de disponibles. On doit donc pouvoir se débrouiller, non ? (Ca ne prouve rien, mais ça donne envie de chercher encore un peu...)

On peut placer d'office un 1 sur chaque cube, et un 2 sur trois des quatre cubes. Ensuite, il faut se débrouiller avec les 0, et leurs interactions avec les autres chiffres. Il en faut forcément un sur le cube qui ne porte pas de 2 (pour le 22 février). Pour la suite, je n'ai rien trouvé de mieux que le bidouillage pur et simple. J'arrive, en plaçant un 0 de plus (sur la face encore dispo), aux cubes suivants :

0 1 2 3 4 5
0 1 2 3 4 5
0 1 6 7 8 9
1 2 6 7 8 9

Pas si simple que ça, mais je pense que ça fonctionne.

langelotdulac a écrit:

Pour plus de commodités appelons nos cubes Robert et Maurice 

Pas mal le coup du 6 retourné ... Et moi qui cherchais un moyen de montrer que ce n'était pas possible
Par contre je me demande si la version de Mathias n'est pas correcte, les 06/06,06/09,09/06, et 09/09 sont possibles, déjà.

C'est ce que j'essayais de montrer, mais sans succès.

J'en connais un qui va être déçu

Bien joué pour l'astuce !

Bonjour

Je souhaite faire un calendrier perpétuel a l'aide de 2 cubes à 6 faces

Comment faire car avec la technique du 6 retourne pour faire le 9, sur le même cube.
Cela ne fonctionne pas

Avez vous la solution ?

dhrm77 a écrit:

Je pense qu'ont peut le faire avec ces 4 cubes:
0-1-2-3-4-5
0-1-6-7-8-9
1-2-3-4-5-6
1-2-3-7-8-9

La version de dhrm ne fonctionne pas car on ne peut pas faire le 06/06

J'ai l'impression que sans l'astuce du "6 retourné" c'est impossible.

Edit : ... Ah mais oui, gwen a prouvé que c'était impossible. Bref, je le cite deux fois de deux posts ! Merci gwen, heureusement que tu étais là !