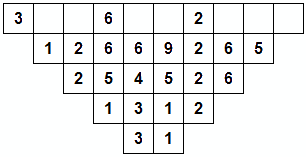
C'est à mon avis quasi impossible sans la fonction donnée, et avec la fonction c'est amusant 
Spoiler : [Afficher le message]
J'appelle A, B, C, D, E, F, G les 7 chiffres manquants de la première ligne, dans cet ordre.
On va déjà placer le 0 en fin de première ligne, car un modulo 0 ne rime pas à grand chose.
G=0
Ensuite, le (modulo 1) + 1 ne peut donner que 1, en début de seconde ligne donc, d'où le 1 est en seconde position de la première ligne.
A=1
De la même manière je ne peux obtenir 9 qu'avec (modulo 9) + 1
D'où D=9
(12+62)modB+1=2
soit 37=1modB ou encore B divise 36
Les seules possibilités pour seraient : 1,2,3,4,6,9. Mais seul 4 n'est pas encore pris.
D'où B=4
(42+C2)mod6+1=6
ce qui donne C2=1[6]
Parmi les possibilités restantes, 5 7 8, seuls 5 et 7 conviennent.
Avec la case suivante, je dois avoir (62+92)modC=5
cad C divise 112
Seul 7 remplit cette condition.
D'où C=7
Il ne reste plus que 8 et 5 à placer. Or (22+F2)modE=5.
J'en déduis que E est supérieur strict à 5.
D'où E=8
et F=5
La pyramide complète est donc :
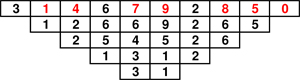
As-tu un mode opératoire qui aurait pu nous amener à trouver la fonction f ? Parce que j'avais un peu cherché, mais je n'y aurais jamais pensé !
Accueil
.
à LOOping, le premier arrivé à bout de cette énigme.
!)
