Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 22-07-2011 19:01:25
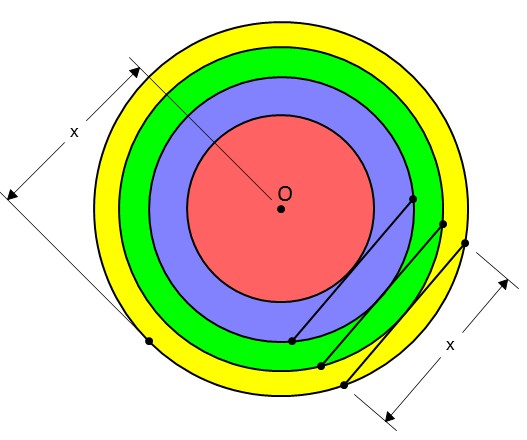
récurrence géoméyriqueJe pars d'un cercle de rayon x et de centre O et j'applique un petit programme de construction :
#0 Pub#2 - 22-07-2011 20:00:29
récutrence géométriqueDans ce cas précis: x^2 = x^2 / 4 + (ax)^2 : a étant le coefficient de réduction #3 - 22-07-2011 21:29:27
récurrence géométroqueLe cercle initial a pour diamètre x et non le rayon. The proof of the pudding is in the eating. #4 - 22-07-2011 21:53:36#5 - 22-07-2011 21:55:59#6 - 23-07-2011 13:20:10
Récurrece géométriqueEn appelant r le rayon d'un cercle, r' le rayon du cercle suivant et "a" la moitié de l'angle formé par la corde par rapport au centre, on a : #7 - 23-07-2011 17:33:42
Récurrence géomériquePartant du centre, avec une corde de longueur x, les rayons sont successivement #8 - 23-07-2011 21:20:59#9 - 23-07-2011 21:28:27
Récurrence gémoétriqueVoici la fonction appliquée à chaque itération : Je ne vien sur se site que pour faire croir que je suis treise intélligens. #10 - 24-07-2011 21:50:58
Récurence géométriqueIl faut 75 itérations pour obtenir un cercle de rayon x/2 avec une corde de x/5... Pour trouver cela, il faut appliquer le théorème de Pythagore. #11 - 24-07-2011 22:05:56
écurrence géométriquePlus intéressant comme résultat. Partons d'un cercle de rayon x et on choisit une longueur de corde de x/n (avec n∈N) alors pour obtenir un cercle de rayon x/2, il faut 3n2 itérations. #12 - 24-07-2011 22:53:16#13 - 24-07-2011 23:37:11
Récurrence géomértique75 étapes si je ne me trompe pas. #14 - 26-07-2011 20:18:26
Récurrence géométriqeMerci pour votre participation! Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.